
Лекции по дифференциальным уравнениям (Абрамов А.А
.).pdf1. Предисловие |
1 |
Лекции по дифференциальным уравнениям. Абрамов Александр Александрович
1. Предисловие
Перед вами курс лекций по дифференциальным уравнениям, читаемый профессором А.А. Абрамовым для 2 курса студентов МФТИ. Хочется отметить, что несмотря на почтенный возраст, А.А. в душе совсем как реб¼нок (и это комплимент). Он будет искренне радоваться вместе с вами каждой доказанной теореме, а его лекции практически не содержат скучных формулировок типа для любой функции, непрерывной в точке, и имеющей непрерывную частную производную в замыкании некоторой области... . Все условия так или иначе комментируются, по возможности приводятся контрпримеры.
Вопрос: Как распечатать 120 страниц? o_O
Ответ: Есть программы, которые готовят к печати брошюры, в итоге получится всего 30. (Например, FinePrint, или им подобные). Думаю, те, кто готовил шпоры, уже знакомы с этой технологией.
Вопрос: Как и зачем это делалось?
Ответ: Происходило сие прямо на лекции, а потом шлифовалось в промежутках между экзаменами. Программа Latex (читается ла-тех ). А те, кто учился у Тарасова, в идеале даже должны уметь ею пользоваться. Кстати, довольно популярная штука среди технарей. РисункиOpenOffice Draw. Они довольно корявые, но других пока нету.
Зачем понятия не имею. Идею мне подал один первокур с ФИВТа, который занимался примерно тем же. А потом как-то сложно было остановиться. Этот эпический труд мне помогли сделать Саня Катруца, Женя Капаев, Наташа Харченко, Женя Вдовина, Александр Гасников, а сам я на тот момент Сер¼жа Довгаль, студент 074 группы.
Вопрос: Если наш¼л опечатку.
Ответ: Разумная мысль заключается в том, чтобы коллекционировать опечатки на google.docs и периодически обновлять.
2 |
ГЛАВА 1. МЕТОДЫ РЕШЕНИЯ НЕКОТОРЫХ УРАВНЕНИЙ. |
Глава 1. Методы решения некоторых уравнений.
1. Основные понятия
В этом параграфе все величины вещественные.
1. Дифференциальные уравнения первого порядка.
Определение: Обыкновенным дифференциальным уравнением первого порядка называется уравнение
f(t; y; y0) = 0 |
(1); |
где t некоторая переменная, y(t) некоторая заданная функция.
Определение: Функция y = '(t) решение (1), если:
1.y(t) определена на некотором промежутке ( ; ), [ ; ], [ ; ), или ( ; ].
2.'0(t) непрерывна на ( ; ), [ ; ], [ ; ), или ( ; ] соответственно.
3.f(t; '(t); '0(t)) = 0 на ( ; ), [ ; ], [ ; ), или ( ; ] соответственно.
Определение: Функция
y = '(t; c) |
(2) |
где c параметр, то есть произвольный коэффициент, общее решение уравнения (1), если
1.Для любого c функция (2) решение,
2.Конкретное решение (1) может быть получено по общему решению (2) при соответствующем выборе c.
Область определения рассматриваемых функций не уточняется.
2. Уравнение, разрешенное относительно производной.
y0 = f(t; y) |
(3) |
называется дифференциальным уравнением первого порядка, разрешенным относительно производной. f определена в некоторой области Gx;y (или замкнутой области).
Определение: Поле направлений множество таких кривых, что график решения огибает поле направлений (касается в каждой точке). При этом график решения не единственный.
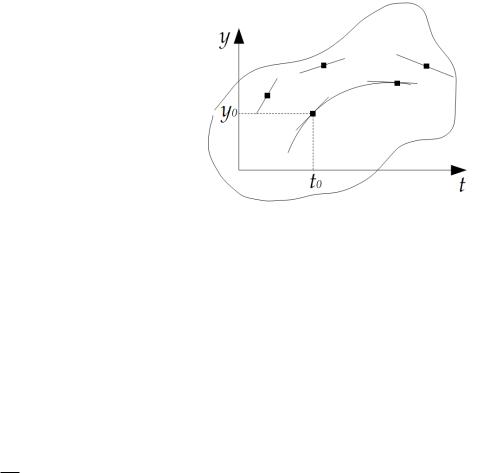
1. Основные понятия |
3 |
Задача Коши для (3):
Первая формулировка. Заданы числа t0, y0, ïðè ýòîì (t0; y0) 2 G; G область. Найти то решение y(t) уравнения (3), которое удовлетворяет условию
y(t0) = y0 |
(4) |
Вторая формулировка. В области G задана точка. Найти то решение уравнения (3), график которого проходит через эту точку.
Теорема: Рассмотрим в области G уравнение (3). Пусть (t0; y0) 2 G. Кроме того, пусть f и
@f
@y
непрерывны в G. Тогда:
1.Существует решение уравнения (1), удовлетворяющее условию (4) y(t0) = y0.
2.Åñëè y1(t) è y2(t) решение (3) ^ (4), то y1(t) = y2(t) на пересечении их областей определения.
3.Пусть y = y(x), x = x(y), и рассматривается дифференциальное уравнение вида
p(x; y) dx + q(x; t) dy = 0 |
(5); |
где p и q определены в Gx;y, в каждой точке G p 6= 0, q 6= 0. Заметим: если на некотором
участке q 6= 0, то (5) , |
dy |
|
p(x; y) |
. Аналогично, если p 6= 0, то (5) |
, |
dx |
|
q(x; y) |
|||
|
= |
|
|
|
|
= |
|
. |
|||
dx |
|
q(x; y) |
dy |
p(x; y) |
|||||||
(5) симметричная форма дифференциального уравнения первого порядка, разреш¼нного относительно производной. Соответствующее решение: H(x; y) = 0, общее решение
H(x; y; c) = 0.
Задача Коши для (5):
В G задана точка, найти то решение, график которого проходит через эту точку.
4 |
ГЛАВА 1. МЕТОДЫ РЕШЕНИЯ НЕКОТОРЫХ УРАВНЕНИЙ. |
2. Уравнение в полных дифференциалах.
В этом параграфе все величины вещественные.
p(x; y) dx + q(x; y) dy = 0 |
(1); |
где p и q определены в области G, и в любой точке G имеет место p 6= 0, q 6= 0.
Определение: Уравнение (1) уравнение в полных дифференциалах, если в G существует функция U(x; y):
dU(x; y) = p(x; y) dx + q(x; y) dy:
Если (5) уравнение в полных дифференциалах, то
(5) |
, |
|
dU(x; y) = 0 , U(x; y) = c; |
c = const: |
|
Задача Коши: x0, y0; c = U(x0; y0), |
U(x; y) = U(x0; y0). |
|
|||
Важные частные случаи (уравнения с разделяющимися переменными): |
|||||
|
|
|
|
a(x) dx + b(y) dy = 0 |
(2) |
a(x) определена и непрерывна на ( ; ), b(x) определена и непрерывна на ( ; ). |
|||||
def |
Z |
a(x) dx какая-либо из первообразных на ( ; ); |
|||
A(x) = |
|||||
def |
Z |
|
b(y) dy какая-либо из первообразных на ( ; ): |
||
B(x) = |
|
||||
U(x; y) = A(x) + B(y). Тогда |
dU(x; y) = A0(x) dx + B0(y) dy = a(x) dx + b(y) dy. |
||||
Z |
a(x) dx + Z |
b(y) dy = c = const решение (2) |
|||
Замечание: Получать U(x; y) = A(x) + B(y) интегрированием уравнения (2) нельзя, так как
в уравнении (2) разные слагаемые придется интегрировать по разным переменным, а такой операции нет.
a(x)m(y) dx + b(y)n(x) dy = 0 |
(3) |
2. Уравнение в полных дифференциалах. |
|
|
|
5 |
||||||||||
Заметим: n(^x) = 0 ) x = x^ решение (3), ибо |
dx = 0, åñëè x^ = const; m(^y) = 0 ) y = y^ |
|||||||||||||
решение (3); |
|
|
|
|
|
|
|
|
|
|
|
|
||
Если в некоторой области m(y) 6= 0 и n(x) 6= 0, то в этой области |
||||||||||||||
|
|
|
|
|
|
|
, |
|
a(x) |
|
b(y) |
|
||
|
|
|
|
(3) |
|
|
|
dx + |
|
= 0; |
||||
|
|
|
|
|
n(x) |
m(y) |
||||||||
то есть уравнение с разделяющимися переменными. |
|
|||||||||||||
Задача: y = y0, G = |
f 1 |
< t < + |
1 |
; |
1 |
|
< y < + . |
|
||||||
|
dy |
|
|
|
|
|
|
1g |
|
|||||
|
|
= y, dy y dt = 0, y 0 решение. При y 6= 0: |
|
|||||||||||
|
dt |
|
||||||||||||
|
|
|
|
dy |
|
|
|
ln(y) t = c; y = ecet; |
||||||
|
|
|
|
|
dt = 0; |
|||||||||
|
|
|
|
y |
||||||||||
ec произвольная ненулевая константа. Общее решение: y = Det, D произвольная константа.
Если заданы t0, y0, òî y0 = Det0 ) |
D = y0e t0 . |
|
|
|
|
|||||||||||||||
|
|
|
|
y(t) = y0et t0 решение задачи Коши. |
|
|
||||||||||||||
Задача: y0 = p3 |
|
, G = f 1 < t < +1; 1 < y < +1g. |
|
|
|
|
||||||||||||||
y2 |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
dy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
= p3 y2; dy p3 2 dt = 0: |
|
|
|
|||||||||
|
|
|
|
|
|
|
dt |
|
|
|
||||||||||
y 0 решение. Если y 6= 0: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
y |
|
|
|
|
|
|
y |
t + c |
3 |
|||||||
|
|
|
d |
|
dt = 0; |
|
|
3 |
|
t = c; y = |
|
: |
||||||||
|
|
|
3 y2 |
|
3 y2 |
3 |
||||||||||||||
|
|
|
p |
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|||
Эта функция удовлетворяет уравнению и при y = 0.
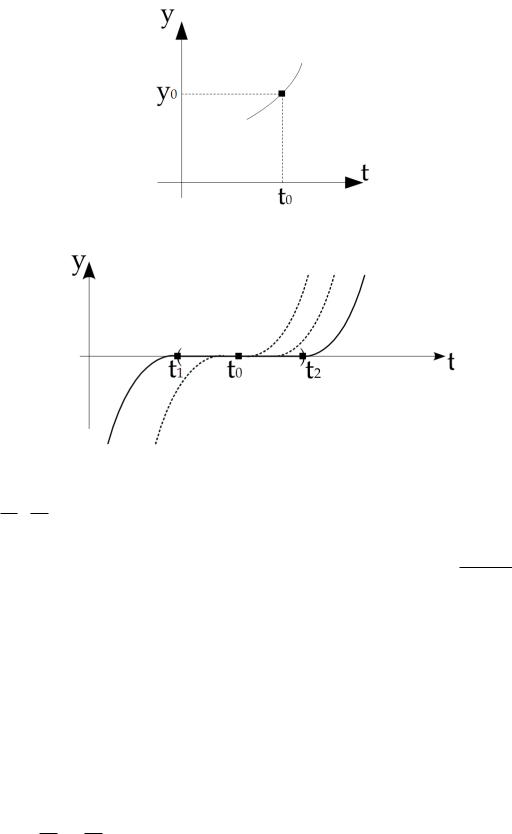
Исследование задачи Коши для второго примера.
t0; y0. y(t): y(t0) = y0.
6 |
ГЛАВА 1. МЕТОДЫ РЕШЕНИЯ НЕКОТОРЫХ УРАВНЕНИЙ. |
1. y0 6= 0. В некоторой окрестности этой точки задача Коши имеет единственное решение.
2. y0 = 0. В любой окрестности этой точки решение задачи Коши не единственно.
Теорема: Пусть в прямоугольнике G = f < t < ; < y < g заданы p(x; y), q(x; y), и, кроме того, p, q, @y@p, @x@q непрерывны в G. Тогда два утверждения равносильны:
n9U(x; y): dU(x; y) = p(x; y) dx + q(x; y) dyo |
, |
n |
@p(x; y) |
|
|||
@y |
Доказательство:
1. ). Åñëè 9U : dU = p dx + q dy, òî p = |
@U |
, q = |
@U |
. |
|
|
|
|
||||||||||||||||
@x |
@y |
|
|
|
||||||||||||||||||||
Затем @y = |
@y |
@x ; |
@x |
= @x |
@y : |
|
|
|
||||||||||||||||
|
|
|
|
@p |
|
@ |
@U |
@q |
@ |
|
@U |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
@x |
||||||
Так как обе смешанные производные непрерывны, то @y |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
@ |
|
@U |
||||||||
|
@p |
= |
@q |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
@y |
@x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
= @q(x; y)o @x
= |
|
@ |
|
@U |
; откуда |
@x |
|
@y |
|||
|
|
|
|||
2. (. Пусть @y@p = @x@q . Построим U(x; y), удовлетворяющую условию. Возьм¼м в G точку
3. Некоторые другие простые типы уравнений первого порядка. |
7 |
(x0; y0). Åñëè @U(x; y) = p(x; y), то положим
@x
x
Z
def
U(x; y) = p( ; y) d + '(y):
x0
Так как должно выполняться q = @U@y , òî
x |
@y |
d + '0(y) = q(x; y) q(x0; y0) + '0(y): |
|
q(x; y) = xZ0 |
|||
|
@p( ; y) |
|
|
|
|
y |
|
'(y): '0(y) = q(x0; y) |
) '(y) = Z |
q(x0; ) d + C; C const: |
|
|
|
y0 |
|
yx
ZZ
U(x; y) = q(x0; ) d + p( ; y0) d + C; C = U(x0; y0):
y0 x0
Геометрическая интерпретация интегрирования:
@y@p = @x@q условие интегрируемости выражения p dx + q dy. (Клод Клеро и Леонард Эйлер)
Определение: '(x; y) интегрирующий множитель выражения p(x; y) dx + q(x; y) dy, если:
1.' не обращается в 0 в рассматриваемой области
2.в рассматриваемой области 9U(x; y): dU = 'p dx + 'q dy.
3. Некоторые другие простые типы уравнений первого порядка.
В этом параграфе все величины вещественные.

8 |
|
|
|
ГЛАВА 1. МЕТОДЫ РЕШЕНИЯ НЕКОТОРЫХ УРАВНЕНИЙ. |
||||
(1) |
dy |
= f |
y |
однородное уравнение. |
|
|
||
|
|
|
|
|||||
dt |
t |
|
|
|||||
f определена и непрерывна на ( ; ). Область значений переменных t; y: |
||||||||
|
|
|
|
|
y |
y |
||
|
|
|
|
G = f0 < t; < |
|
< g [ ft < 0; < |
|
< g: |
|
|
|
|
t |
t |
|||
Метод решения: yt = u новая неявная функция, t независимая переменная.
y = ut; u0t + u = f(u); t |
du |
+ u = f(u); |
|
dt |
|||
|
|
t du + (u f(u)) dt = 0 уравнение с разделяющимися переменными.
(2)ddyt = a(t)y + f(t) линейное уравнение. a(t), f(t) определены и непрерывны на [ ; ].
(3)ddzt = a(t)z линейное однородное уравнение, соответствующее уравнению (2).
dz a(t)z dt = 0:
z(t) = 0 решение. При z 6= 0:
Z
dzz a(t) dt = 0; A(t) = a(t) dt какая-либо первообразная. lnjzj A(t) = C; z(t) = eCeA(t):
eC произвольная ненулевая константа. Общее решение: z(t) = DeA(t), D произвольная
ненулевая константа.
y(t) = eA(t)u(t)
u(t) новая искомая функция. Так как y = eAu, òî u = e Ay.
(eAu)0 = a(eAu) + f; aeAu + eAu0 = aeAu + f; eAu0 = f; u0 = e Af:
Z Z
u = e A(t)f(t) + C; y(t) = eA(t) e A(t)f(t) dt + C :
(Метод Лагранжа вариации постоянной).
Задача: Написать формулу решения задачи Коши при 6 t0 6 ; y0 = y(t0). Рекомендации:
tt
RR
A(t) = a( ) d ; u = : : : + C. C ?
t0 t0
4. Метод введения параметра.
В этом параграфе все величины вещественные.
f(t; y; y0) = 0: |
(1) |
4. Метод введения параметра. |
9 |
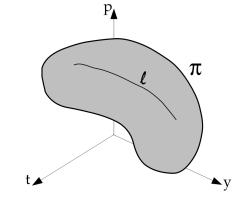
Рассмотрим поверхность в тр¼хмерном пространстве (t; y; p). : f(t; y; p) = 0. На этой поверхности рассмотрим кривую `, соответствующую решению дифференциального уравнения.
`: |
y = y(t) |
. |
|
p = p(t) |
|||
|
|
` график решения (1) |
, |
` |
|
и на ` имеет место dy = p dt, p = y0. |
|
|
|
Задача Коши для (1):
1.На задана точка. Найти то решение уравнения (1), график которого проходит через эту точку.
2.Заданы числа t0; y0; p0, удовлетворяющие условию f(t0; y0; p0) = 0. Найти y(t) то решение, для которого y(t0) = y0, y0(t0) = p0.
Частный случай: y0 = g(t; y).
Все рассматриваемые функции достаточно гладкие, области определения функций не огова-
риваются.
8
t = '( ; )
<
f(t; y; p) = 0 , y = ( ; ) : p = !( ; )
Решаем уравнение dy = p dt в координатах ; .
0 d + 0 d = !('0 d + '0 d )
Получили симметричную форму уравнения, разреш¼нного относительно производной:
( 0 !'0 ) d + ( 0 !'0 ) d = 0
Примеры:
A(y0)t + B(y0)y + C(y0) = 0 уравнение Лагранжа. Предполагаем B 6= 0. Тогда уравнение принимает вид:
y = k(y0)t + b(y0); y = k(p)t + b(p)
10 |
ГЛАВА 1. МЕТОДЫ РЕШЕНИЯ НЕКОТОРЫХ УРАВНЕНИЙ. |
Решаем уравнение dy = p dt в координатах p; t. После дифференцирования:
|
|
|
|
|
k0t dp + k dt + b0 dp = p dt |
|
|
|
|
|
|
(k0t + b0) dp + (k p) dt = 0 |
|
Если находится p^: k(^p) = p^, то p = p^ решение. При k 6= 0: |
||||||
|
|
dt |
+ |
k0t + b0 |
= 0 линейное уравнение. |
|
|
|
|
|
|||
|
|
dp |
|
k p |
||
f(y; y0) = 0, f(y; p) = 0 , |
|
p = !( ) |
||||
|
|
|
|
|
y = ( ) |
|
Решаем уравнение dy = p dt в координатах ; t. |
||||||
|
|
|
|
|
|
0( ) d = !( ) dt |
^ |
^ |
^ |
||||
Если y = ( ) = 0, то = решение, y = ( ) решение. |
||||||
Ïðè !( ) 6= 0 ) t = Z |
!0(( )) d + C. |
|||||
|
|
|
|
|
|
|
f(t; y0) = 0. f(t; p) = 0 ) |
p = !( ) |
|||||
|
|
|
|
|
t = '( ) |
|
5. Уравнения высших степеней.
В этом параграфе все величины вещественные.
1.Понижение порядка уравнения Пусть t независимая переменная, y(t) искомая,
f задана. Уравнение
f t; y; y0; : : : ; y(n) = 0 |
(1) |
называется обыкновенным дифференциальным уравнением порядка n.
Определение: Функция y = '(t) решение (1), если
1.'(t) определена на ( ; ); [ ; ); ( ; ], или [ ; ].
2.'(k)(t) непрерывна на ( ; ); [ ; ); ( ; ], или [ ; ] соответственно.
3.f t; '(t); '0(t); : : : ; '(n)(t) = 0 на ( ; ); [ ; ); ( ; ], или [ ; ] соответственно.
Задача Коши для (1):
Заданы числа t0; q0; q1; : : : ; qn, удовлетворяющие условию f(t0; q0; q1; : : : ; qn) = 0. Найти y(t) решение (1), удовлетворяющее условиям y(t0) = q0, y0(t0) = q1, . . . , y(n)(t0) = qn.
Важный частный случай (1):
y(n) = f(t; y; y0; : : : ; y(n 1)) |
(2) |
