Лекции по дифференциальным уравнениям (Абрамов А.А

Z

p(z0)2 + qz2 dt = 0; z0 0; z 0

Противоречие, z тривиальное решение.

Замечание: (См. п.4 1 Главы 2). Там мы изучали случай квадратичного функционала, и доказали там, что для этого квадратичного функционала уравнение Эйлера имеет вид (3). Если

y есть решение этого уравнения, то он да¼т минимум функционала. Это была единственная

теорема в этом разделе, где давались достаточные условия минимума. Имеет ли это уравнение решение? В первом семестре мы не могли этого доказать. Сейчас мы заполнили этот пробел.

5. Теорема Штурма

Жан Франсуа Штурм французский математик.

В этом параграфе все величины вещественные.

1.Будем рассматривать уравнения

6 t 6 , a(t); b(t) непрерывны на [ ; ].

Замечание: В этом параграфе будут рассматриваться осцилляционные (колебательные) свойства решений. Будет исследоваться, сколько раз нетривиальные решения могут обращаться в ноль.

Важное преобразование уравнения (1). Сделаем замену: y(t) = (t)z(t);

где z(t) новая искомая функция, (t) выбираем мы.

00z + 2 0z0 + a 0z + a z0 + b z = 0

(t) выбираем так, чтобы сумма подч¼ркнутых слагаемых равнялась нулю (избавляемся от членов с первой производной). Решая дифференциальное уравнение, получаем ответ:

= Ce R a(2t) dt

C фиксированная константа, интеграл какая-либо фиксированная первообразная. Возьм¼м какую-либо C 6= 0; (t) не обращается в 0.

114 ГЛАВА 6. ЛИНЕЙНЫЕ УРАВНЕНИЯ С ПЕРЕМЕННЫМИ КОЭФФИЦИЕНТАМИ

Замечание: Запоминать эту формулу не нужно. Нужно запомнить идею (замену y = z). Для строгого обоснования преобразования потребуем ещ¼ a0(t) непрерывна на отрезке [ ; ]. Зачем это надо? После преобразования в уравнение войд¼т вторая производная , которая будет содержать первую производную функции a.

Дальше будем рассматривать однородные линейные уравнения второго порядка без первой производной.

2. Теорема Штурма (Теорема сравнения)

Рассмотрим на [ ; ] два уравнения.

1.z100 + p1(t)z1 = 0

2.z200 + p2(t)z1 = 0

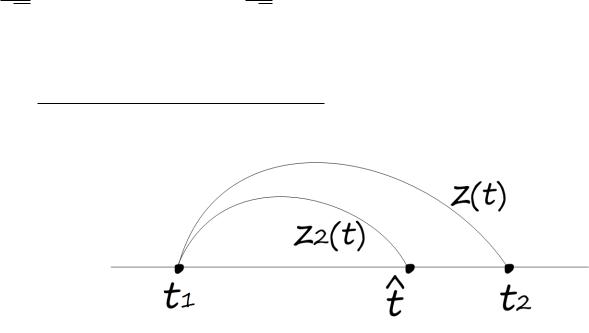
Пусть z1(t); z2(t) нетривиальные решения этих уравнений. Пусть кроме того, p1(t); p2(t) непрерывны на [ ; ] и p1(t) 6 p2(t) для всех t 2 [ ; ]. Пусть t1 è t2 соседние нули z1(t). Тогда z2(t) имеет нуль на (t1; t2) èëè z2(t1) = z2(t2) = 0.

Замечание: Надо обратить внимание, что или не разделительное, а математическое (то есть не является взаимоисключающим).

Доказательство: Докажем, что каждый нуль нетривиального решения

z00 + p(t)z = 0;

где p(t) непрерывна на [ ; ], изолированный. (То есть нули не накапливаются в какой-то

Таким образом, термин соседние нули оправдан.

Доказательство теоремы от противного.

t1 < t2, z1(t) > 0 ïðè t1 < t < t2. z2(t) > 0 ïðè t1 < t < t2, z2(t2) > 0, z2(t1) > 0. Тогда z10 (t1) > 0, z10 (t1) 6= 0.

По тем же причинам z10 (t2) < 0. Тогда

+z1(t1)z20 (t1) + p1(t) p2(t) z1(t)z2(t) dt = 0

Получено противоречие (0 < 0). Теорема Штурма доказана.

3.

6 t 6 , p(t) непрерывна на [ ; ].

Из теоремы Штурма следуют несколько важных утверждений:

Теорема: Пусть z1(t) è z2(t) фундаментальная система решений уравнения (2). Тогда нули z1(t) è íóëè z2(t) перемежаются. (Между соседними нулями z1 åñëè íóëü z2).

Доказательство: Прежде всего докажем, что два линейно независимых решения не могу

p(t) > p(t):

116 ГЛАВА 6. ЛИНЕЙНЫЕ УРАВНЕНИЯ С ПЕРЕМЕННЫМИ КОЭФФИЦИЕНТАМИ

z2(t) имеет нуль на t1; t2. Теорема доказана.

Теорема: Пусть p(t) 6 0. Тогда нетривиальное решение z(t) уравнения (2) может иметь не более одного нуля на отрезке [ ; ].

Доказательство: (от противного).

z00 + p(t)z = 0; t1; t2 íóëè z(t) z200 + 0 z2 = 0; z2(t) 1:

p(t) 6 0, z2(t) имеет нуль на [t1; t2], противоречие.

Теорема: Пусть m 6 p(t) 6 M на отрезке [ ; ], где m; M положительные числа. Тогда

расстояние между соседними нулями нетривиального решения z(t) уравнения (2) не меньше pM и на каждом отрезке длины pm есть нуль этого решения.

Доказательство:

2.Второе утверждение доказать самим. Надо воспользоваться теоремой Штурма и сопоставить два уравнения системы.

4.Об уравнении Бесселя.

Замечание: Бессель астроном, также занимавшийся математикой.

число.

Замечание: Сейчас мы изучим осцилляционные свойства этого уравнения. Прежде всего заметим, что надо рассматривать уравнение при t > 0 или при t < 0. При t = 0 уравнение

имеет особенность. Можно изучать, как вед¼т себя уравнение в окрестности особой точки, но это не та проблема, которой мы сейчас занимаемся.

Пусть, для определ¼нности 0 < t.

Теорема: Нетривиальное решение уравнения Бесселя имеет на (0; +1) бесконечное число нулей. При этом расстояние между соседними нулями стремится к при уходе в +1 .

Доказательство: Для начала, сделаем замену из п.1, y(t) = (t)z(t). После подстановки в