4.4. Двойственный симплекс-метод

В разд. 4.2 было показано, что при решении прямой задачи на любой итерации разность (z_j—cj), т. е. величина z-коэффициента при переменной х_j равна разности между левой и правой частями, соответствующего ограничения двойственной задачи. Если при решении прямой задачи с максимизируемой целевой функцией итерация не приводит к оптимальному решению, то по крайней мере для одной переменной z_j—с_j<0 и только в оптимуме для всех j разность z_j—с_j 0.

Рассматривая это условие с учетом двойственности, можно записать

Эти результаты позволяют разработать новый метод решения задач ЛП, при использовании которого сначала получается недопустимое, но «лучшее, чем оптимальное», решение. (Сравните с обычным симплекс-методом, при котором сначала находится допустимое, но неоптимальное решение.) Новый метод, получивший название двойственного симплекс-метода, обеспечивает выполнение условия оптимальности решения и систематическое «приближение» его к области допустимых решений. Когда полученное решение оказывается допустимым, итерационный процесс вычислений заканчивается, так как это решение является и оптимальным. Такой метод решения подходит для определенного класса задач ЛП, но важнее то, что он непосредственно используется при анализе моделей на чувствительность. (Этот вопрос будет рассмотрен в следующем разделе.)

Пример 4.4.1

Минимизировать z=2x₁+x₂

при ограничениях

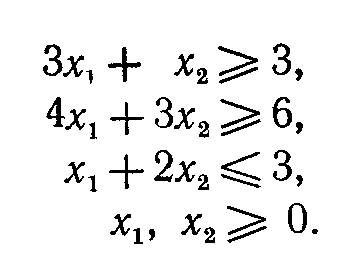
Сначала необходимо преобразовать все ограничения в неравенства со знаком , а затем ввести остаточные переменные. Выполнив эти процедуры, приходим к следующей формулировке задачи:

минимизировать z=2i+2 при ограничениях

Начальная симплекс-таблица, соответствующая оптимальному, но недопустимому решению, имеет вид

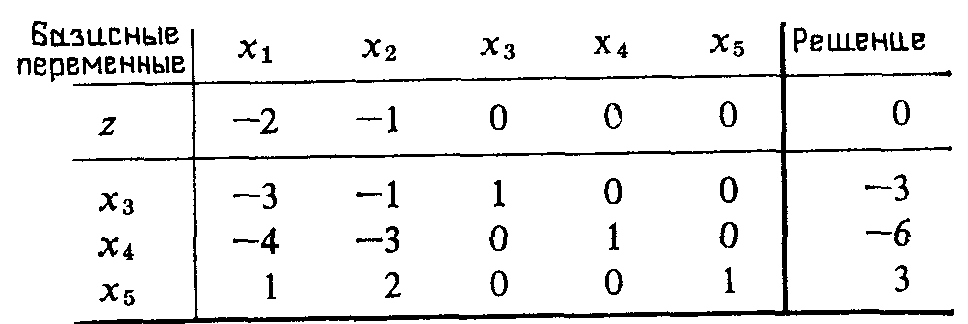
Как и обычный симплекс-метод, рассматриваемый метод решения основан на использовании условий оптимальности и допустимости. Выполнение условия оптимальности гарантирует оптимальность последовательно получаемых решений, а выполнение условия допустимости обеспечивает итерационное приближение к области допустимых решений.

Условие допустимости. В качестве исключаемой переменной выбирается наибольшая по абсолютной величине отрицательная базисная переменная. (При наличии альтернатив выбор делается произвольно.) Если все базисные переменные неотрицательные, процесс вычислений заканчивается, так как полученное решение допустимое и оптимальное.

Условие оптимальности. Включаемая в базис переменная выбирается из числа небазисных переменных следующим образом. Вычисляются отношения коэффициентов левой части z-уравнения к соответствующим коэффициентам уравнения, ассоциированного с исключаемой переменной. Отношения с положительным или нулевым значением знаменателя не учитываются. В задаче минимизации вводимой переменной должно соответствовать наименьшее из указанных отношений, а в задаче максимизации — отношение, наименьшее по абсолютной величине. (При наличии альтернатив выбор делается произвольно.) Если знаменатели всех отношений равны нулю или положительные, задача не имеет допустимых решений.

После выбора включаемой в базис и исключаемой переменных для получения следующего решения осуществляется обычная операция преобразования строк симплекс-таблицы.

В приведенной выше таблице исключаемой переменной является x₄(=—6), так она имеет наибольшее по абсолютной величине отрицательное значение. Отношения, вычисленные для определения новой базисной переменной, приведены в следующей таблице:

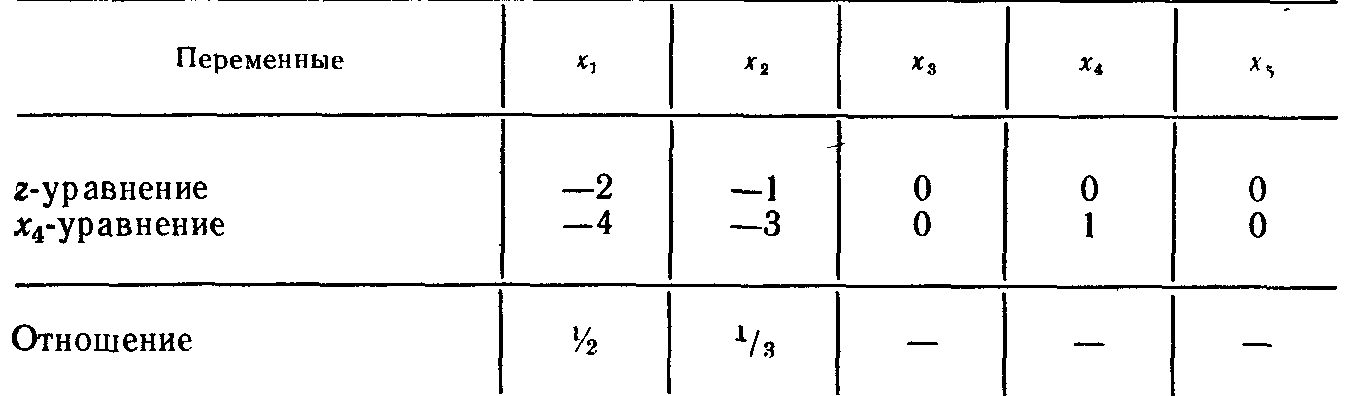
В качестве включаемой переменной выбирается х₂ так как этой переменной соответствует наименьшее отношение, равное 1/3. Последующее преобразование строк приводит к новой симплекс-таблице -

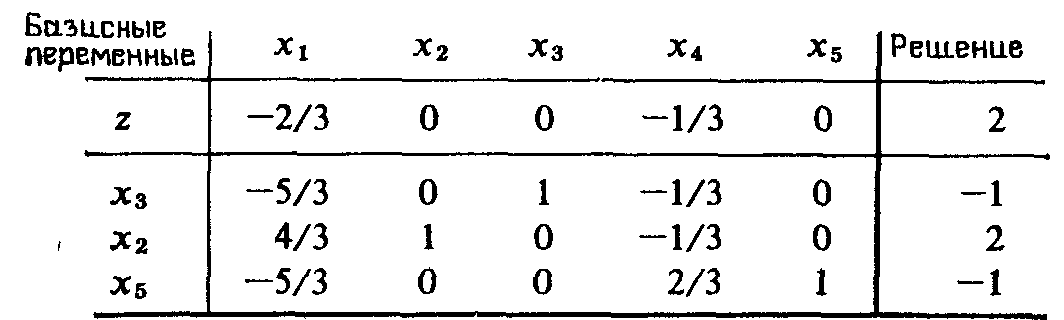
Новое решение также оптимальное, но все еще недопустимое (х₃=—1, х₅=—1). Если в качестве новой исключаемой переменной выбрать (произвольно) х₃, вводимой в базис переменной будет х₁,. и в результате будем иметь следующую симплекс-таблицу;

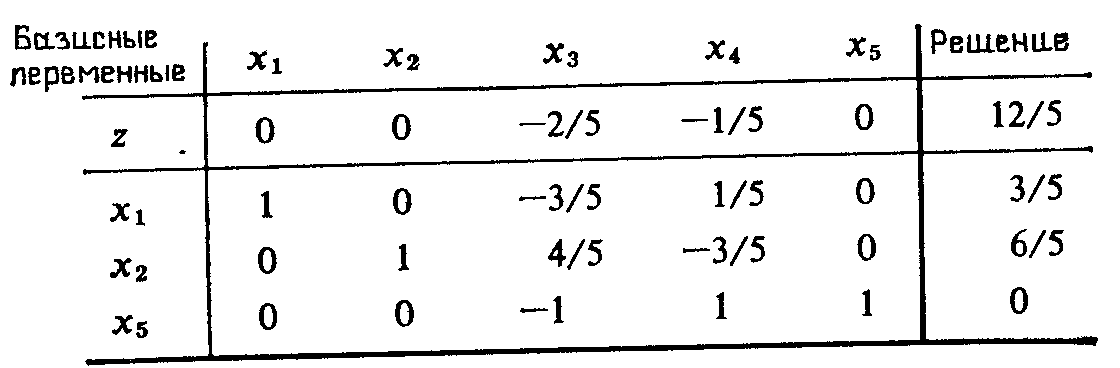
Полученное решение является оптимальным и допустимым.

Применение двойственного симплекс-метода особенно эффективно при анализе моделей на чувствительность, в частности в тех случаях, когда после получения оптимального решения в условия задачи вводится новое ограничение. Если для предыдущего оптимального решения новое ограничение не выполняется, то полученное решение оптимальное, но недопустимое. В этом случае двойственный симплекс-метод используется для нахождения нового оптимального решения путем последовательного уменьшения «степени недопустимости» решений, получаемых в процессе симплекс-итераций.