Лекция № . Линейное программирование: двойственность и анализ моделей на чувствительность

В данной вводится новое понятие теории ЛП — понятие двойственности. Будучи исключительно важным в теоретическом отношении, оно представляет также и большой практический интерес, поскольку используется при разработке эффективных методов анализа моделей на чувствительность. Основы такого анализа в упрощенном изложении уже были даны в подразд. 2.1.2 и разд. 3.4. Материал настоящей главы, в которой приемы анализа моделей на чувствительность рассматриваются с использованием понятия двойственности, поможет в полной мере оценить практическую важность этого анализа. Кроме того, ознакомление с соответствующими теоретическими положениями позволит глубже понять некоторые новые и весьма эффективные вычислительные мётоды, рассматриваемые в этой и последующих главах.

1. Определение двойственной задачи

Двойственная задача — это вспомогательная задача ЛП, формулируемая с помощью определённых правил непосредственно из условий исходной, или прямой, задачи. В литературе по ЛП в большинстве случаев рассматриваются формулировки двойственной задачи, соответствующие различным формам прямой задачи, которые в свою очередь определяются типом ограничений, знаками переменных и направлением оптимизации (максимизация или минимизация). Опыт показывает, что на начальной стадии изучения теории ЛП детали различных формулировок двойственной задачи нередко затрудняют восприятие материала. Кроме того, практическое использование теории двойственности на самом деле и не требует знания деталей различных формулировок двойственной задачи.

В данной книге дается обобщенная формулировка двойственной задачи ЛП, которая применима к любой форме представления прямой задачи. В основу такой формулировки положен тот факт,: что использование симплекс-метода требует приведения любой задачи ЛП к стандартной форме (разд. 3.1). Так как все методы вычислений, основанные на соотношениях двойственности, предполагают непосредственное использование симплекс-таблиц, формулировка двойственной задачи в соответствии со стандартной формой прямой задачи представляется достаточно логичной. Как будет показано

ниже, при такой формулировке двойственной задачи автоматически учитываются знаки двойственных переменных, что в других случаях нередко вызывает недоразумения. Следует, однако, помнить, что приводимая ниже формулировка двойственной задачи является обобщенной в том смысле, что она применима ко всем формам прямой задачи.

Прямая задача ЛП в стандартной форме записывается следующим образом:

(максимизировать или минимизировать )

при ограничениях

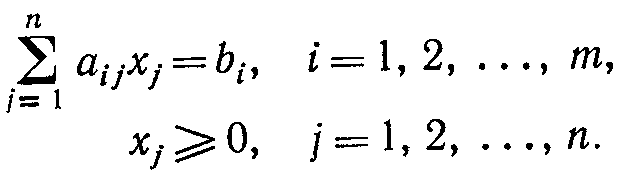
Заметим, что в состав п переменных х_j включаются также избыточные и остаточные переменные. Чтобы сформулировать условия двойственной задачи, расположим коэффициенты, фигурирующие в условиях прямой задачи, так, как схематически показано в табл. 4.1.

Таблица 4.1

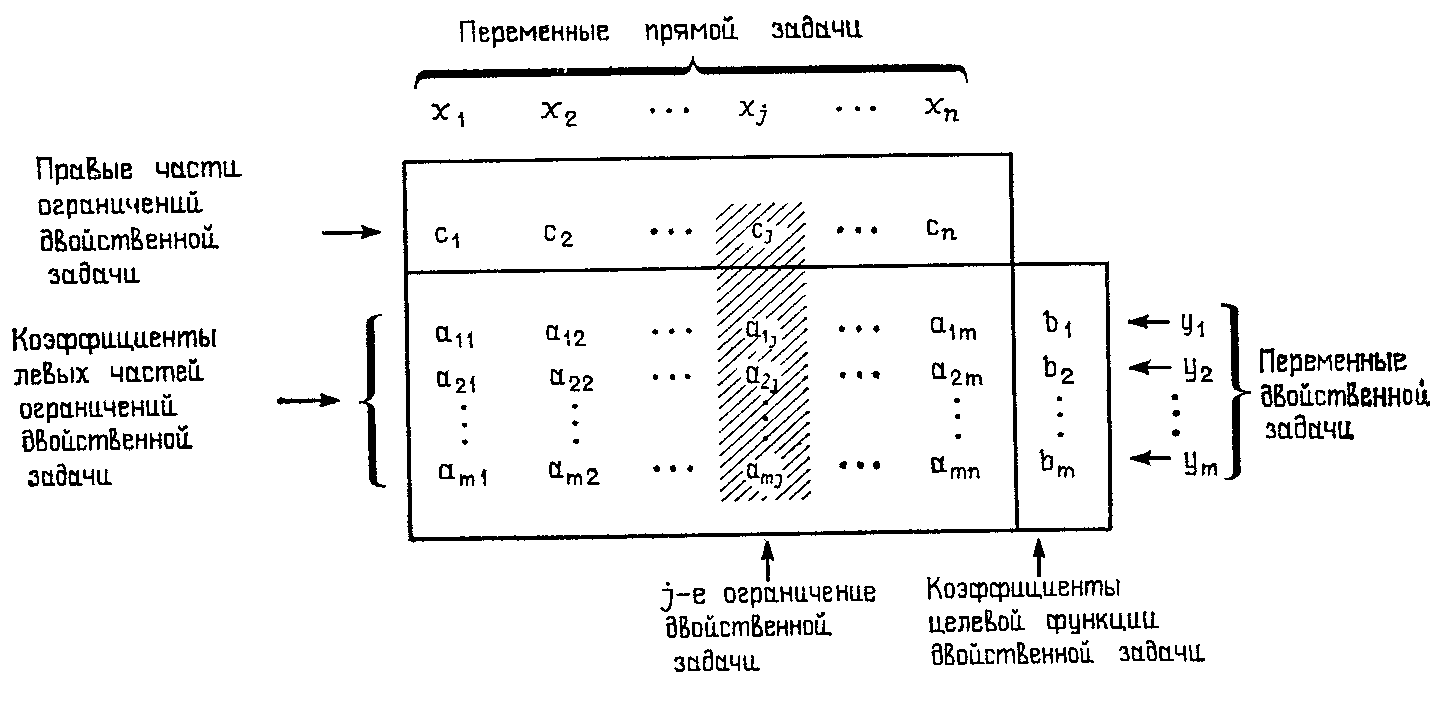
Из приведенной схемы следует, что двойственная задача получается путем симметричного структурного преобразования условий прямой задачи в соответствии со следующими правилами:

1) каждому ограничению прямой задачи соответствует переменная двойственной задачи;

2) каждой переменной прямой задачи соответствует ограничение двойственной задачи;

3) коэффициенты при некоторой переменной, фигурирующие в ограничениях прямой задачи, становятся коэффициентами левой части соответствующего ограничения двойственной задачи, а коэффициент, фигурирующий при той же переменной в выражении для целевой функции прямой задачи, становится постоянной правой части этого же ограничения двойственной задачи (см., например, заштрихованный столбец, соответствующий в табл. 4.1 переменной х,).

Из указанных правил построения двойственной задачи следует, что она имеет т переменных (y₁, y₂, …, y_т) и n ограничений (соответствующих п переменным прямой задачи (x₁, x₂,…,х_n).

Рассмотрим теперь, как формируются остальные условия двойственной задачи: направление оптимизации, ограничения и знаки двойственных переменных. Информация по этим вопросам применительно к максимизируемой и минимизируемой целевым функциям задачи в стандартной форме представлена в табл. 4.2. Напомним, что в стандартной формулировке прямой задачи все ограничения записываются в виде равенств (с неотрицательной правой частью), а все переменные неотрицательные. Поэтому существенным различием прямых задач, записанных в стандартной форме, является только направление оптимизации.

Таблица 4.2

Прямая задача в стандартной форме *) Целевая функция	Двойственная задача
	Целевая функция	Ограничения	Переменные
Максимизация	Минимизация		Не ограничены в знаке
Минимизация	Максимизация		Не ограничены в знаке

Примеры, которые рассматриваются ниже, служат иллюстрациями использования приведенных выше правил построения двойственной задачи и (что более важно) показывают применимость обобщенной формулировки двойственной задачи ко всем формам представления условий прямой задачи.

Пример 4.1.1. Прямая задача:

максимизировать

при ограничениях

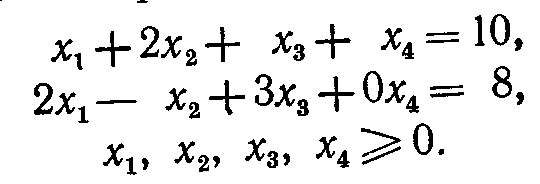
Заметим, что x₄ — остаточная переменная, введенная в первое огра­ничение. Поэтому, коэффициенты, фигурирующие при этой пере­менной в целевой функции и во втором ограничении, равны нулю.

Двойственная задача:

минимизировать =10y₁+8y₂

при ограничениях

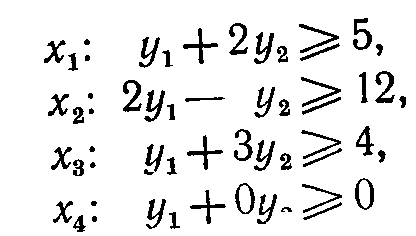
(означает, что y₁0),

y_1, y₂ не ограничены в знаке

Следует отметить, что условие y₁0 является более жестким, чем условие неограниченности y₁ в знаке. Поэтому при исключении этой избыточности ограничений двойственная задача формулируется сле­дующим образом:

минимизировать =10y₁+8y₂

при ограничениях

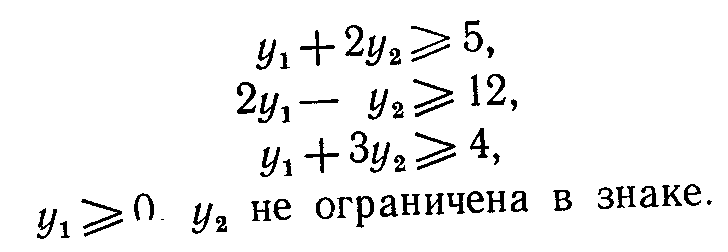
y₁0 не ограничена в знаке

Упражнение 4.1.1. Измените условия сформулированной выше двойственной задачи применительно к случаю минимизации целевой функции прямой задачи. {Ответ. Изменения сводятся к следующему: w подлежит максимизации, знак неравенства в первых трех ограничениях изменяется на противополож­ный (), y₁0}

Пример 4.1.2. Прямая задача:

минимизировать z=5x₁—2x₂ при ограничениях

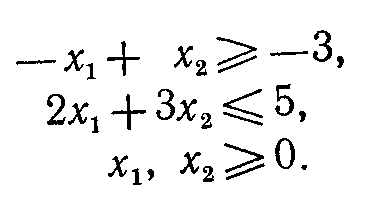
Прямая задача в стандартной форме:

минимизировать z=5x₁—2x₂ при ограничениях

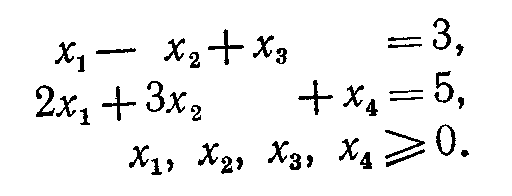
Двойственная задача:

максимизировать =3y₁+5y₂ при ограничениях

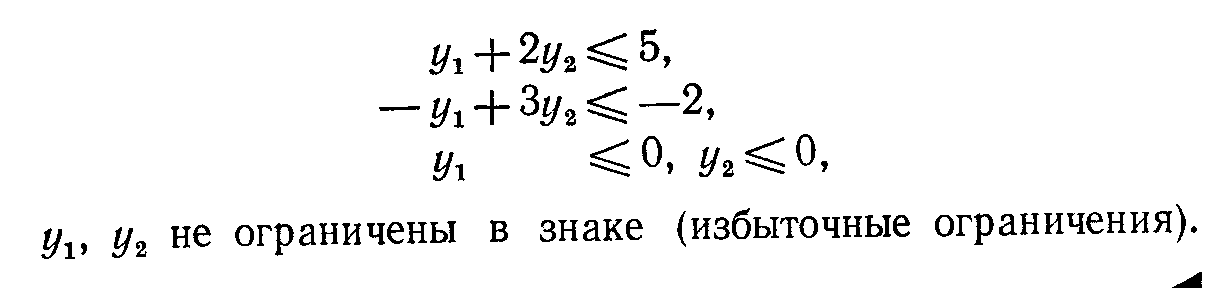
Упражнение 4.1.2. Как изменятся 'условия сформулированной выше двой­ственной задачи, если знак неравенства () во втором ограничении прямой задачи изменится на противоположный [Ответ. Ограничение y₂0 примет вид y₂0.]

Пример 4.1.3. Прямая задача:

максимизировать z=5x₁+6x₂ при ограничениях

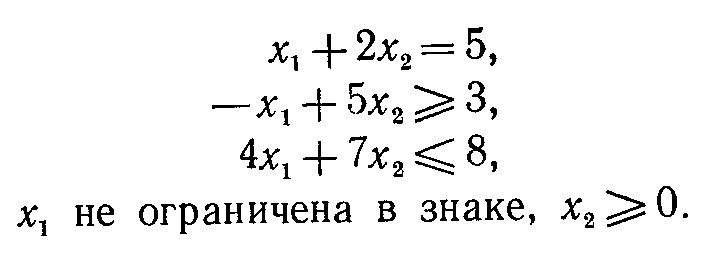
Прямая задача в стандартной форме

Пусть x₁=x₁-x₁ где x_1, x₁0. Стандартная формулировка прямой задачи при использовании такой подстановки имеет вид

максимизировать x₁=5x₁-6x₁+6x₂ при ограничениях

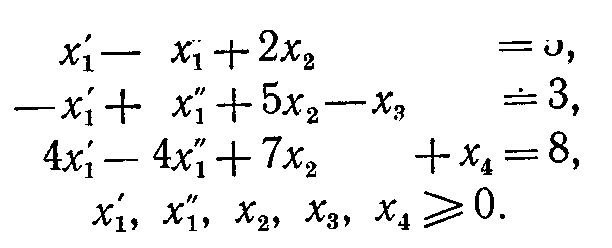
Двойственная задача:

минимизировать =5y₁+3y₂+8y₃

при ограничениях

Заметим, что первое и второе ограничения двойственной задачи можно (но не обязательно) заменить одним ограничением в виде равенства y₁-y₂+4y₃=5 (см. разд. 3.1). Такая замена возможна всякий раз, когда переменная прямой задачи не ограничена в знаке, т. е. неограниченность в знаке переменной прямой задачи всегда обусловливает появление ограничения двойственной задачи в виде равенства (а не неравенства) как при максимизации, так и минимизации целевой функции прямой задачи.

Упражнение 4.1.3. Покажите, как изменится сформулированная выше двойственная задача, если в прямой задаче целевая функция подлежит минимизации, а первое ограничение записано как неравенство вида .

Если тщательно проанализировать содержащиеся в данном разделе примеры, то все правила, которые обычно приводятся в литературе по ЛП в связи с формулировкой двойственной задачи, можно получить самостоятельно. Однако в этом случае придется рассматривать множество разнообразных условий, в частности знаки двойственных переменных. Если же следовать двум простым правилам, содержащимся в табл. 4.2, затруднений такого рода не возникает. При этом следует иметь в виду, что приведение прямой задачи к стандартной форме не является какой-то «дополнительной» работой, поскольку для реализации начальной итерации симплекс-метода такая форма записи исходной задачи является обязательной.

Упражнение 4.1.4. Покажите, что ограничение двойственной задачи, ассоциированное с искусственной переменной (R_i), фигурирующей в условиях стандартной прямой задачи, всегда будет избыточным. Следовательно, формулируя двойственную задачу, нет необходимости учитывать ограничение, связанное с искусственной переменной исходной задачи.

[Ответ. Ограничение двойственной задачи, соответсгвующее искусственной переменной (R_i), при максимизации целевой функции прямой задачи имеет вид y_i-М, а при минимизации записывается как y_iМ . Оба ограничения всегда избыточные, так как М может быть сколь угодно большим положительным числом.]