2. Соотношения двойственности

В данном разделе будет показано, что между прямой и двойственной задачами существует тесная взаимосвязь. Фактически оптимальное решение одной из этих задач непосредственно (без каких-либо дополнительных вычислений) можно получить из данных симплекс-таблицы для оптимального решения другой задачи. Кроме того, будут представлены некоторые вычислительные процедуры, использующие соотношения двойственности и позволяющие выявить изменения оптимального решения прямой задачи, обусловленные изменениями исходной модели. Это облегчит изучение материала в разделе, посвященном методам анализа моделей на чувствительность.

4.2.1. Получение оптимального решения двойственной задачи с помощью симплекс-таблиц

Чтобы показать, каким образом оптимальное решение двойственной задачи можно получить непосредственно из симплекс-таблиц для оптимального решения прямой задачи, воспользуемся задачей, сформулированной в примере 4.1.1. Для удобства изложения воспроизведем условия прямой и соответствующей ей двойственной задач.

Прямая задача	Двойственная задача
Максимизировать z = 5x1 +12x2 + 4x3	минимизировать w= 10y1+8y2
при ограничениях	при ограничениях
Х1+X2+Xз10,	y1+y25
2Х1-X2+3Xз=8,	2y1-y212
X1, X2, X3 0	y1+3y24
	Y10, y2 не ограничен в знаке.

Решим сначала с помощью симплекс-метода обе сформулированные задачи независимо. Сравнение симплекс-таблиц для оптимальных решений задач покажет, каким образом оптимальное решение одной задачи можно непосредственно получить из оптимального решения другой задачи. В табл. 4.3 представлены итерации симплекс-метода, обеспечивающие получение оптимального решения прямой задачи. Результаты всех итераций приведены полностью, так как в дальнейшем еще потребуется обращение к этой информации. Начальная и завершающая (соответствующая оптимуму) итерации для двойственной задачи представлены в табл. 4.4. Для получения начального решения прямой задачи необходимо введение искусственных переменных. Кроме того, для переменной у'г двойственной задачи, не имеющей ограничения в знаке, используется подстановка У₂=У₂—У_2, где У₂ и У₂ — неотрицательные переменные.

Таблица 4.3

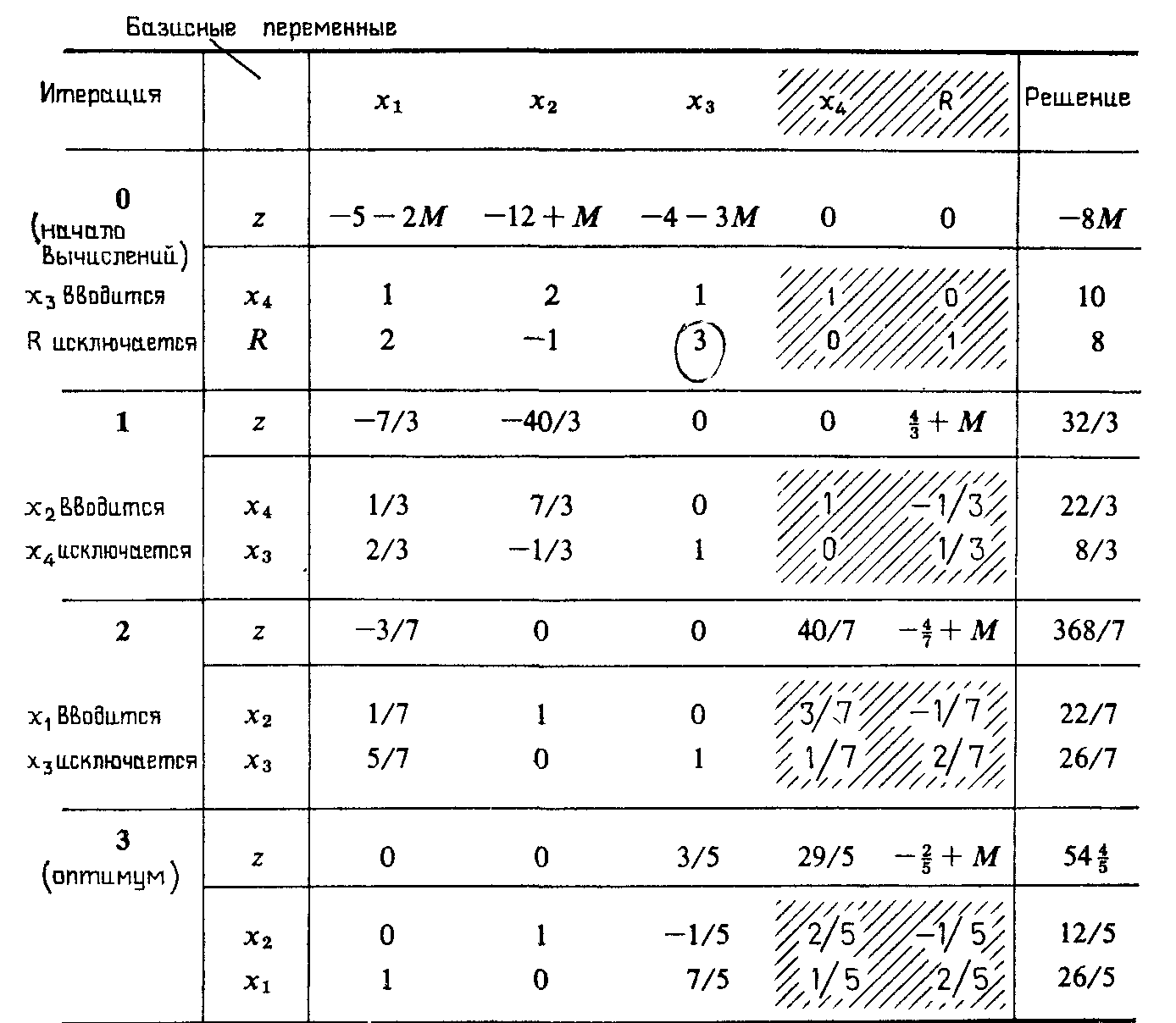
Оптимальное решение двойственной задачи, полученное с помощью симплекс-метода, приведено в табл. 4.4: ω=54⁴/₅, y₁=29/5, У₂=У₂—У₂=о—2/5=—2/5. Этот же результат можно получить и непосредственно из симплекс-таблицы для прямой задачи (табл. 4.3), если воспользоваться следующим уравнением:

Эти данные удобно представить в следующей форме:

Используя приведенное выше уравнение, получим

откуда y₁=29/5 и y₂=—2/5, что полностью соответствует данным, представленным в симплекс-таблице для оптимального решения двойственной задачи.

Таблица 4.4

Покажем, что оптимальное решение прямой задачи в свою очередь также непосредственно определяется из симплекс-таблицы для оптимального решения двойственной задачи (см. табл. 4.4) при использовании приведенного выше уравнения. Заметим, что переменные x_1, x₂ и x₃ связаны с первым, вторым и третьим ограничениями двойственной задачи соответственно и, следовательно, с искусственными переменными R_1,R₂ и R₃.

Из приведенных в таблице данных следует, что

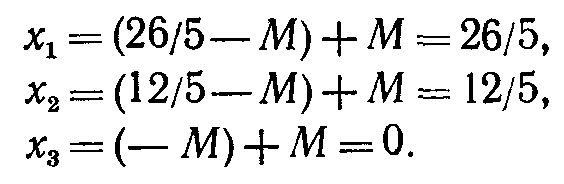
Таким образом, получен тот же результат, который приведен в симплекс-таблице для оптимального решения прямой задачи (табл. 4.3).

Заинтересованность в определении оптимального решения прямой задачи путем решения двойственной к ней задачи обусловлена тем, что вычисления, необходимые для решения двойственной задачи, могут оказаться менее сложными, чем для прямой задачи. Напомним, что трудоемкость вычислений при решении задач ЛП в большей степени зависит от числа ограничений, чем от количества переменных. Поэтому, если в двойственной задаче ограничений меньше, чем в прямой, как правило, целесообразнее решать двойственную задачу и полученный результат использовать для нахождения оптимального решения прямой задачи.

Анализ и сопоставление результатов, полученных при решении прямой и двойственной задач (табл. 4.3 и 4.4), позволяют сформулировать два интересных вывода.

1. На итерации, приводящей к оптимуму,

Это равенство справедливо всегда и фактически соответствует оптимальным значениям переменных обеих задач, а именно:

2. В задаче максимизации (табл. 4.3) целевая функция последовательно увеличивается от начального значения z=—8M до оптимального z=54⁴/₅. В задаче минимизации (табл. 4.4) целевая функция последовательно уменьшается от начального значения ω=21M до оптимального ω=54⁴/₅. Этот вывод иллюстрирует рис. 4.1. Приведенная схема указывает на то, что значение целевой функции

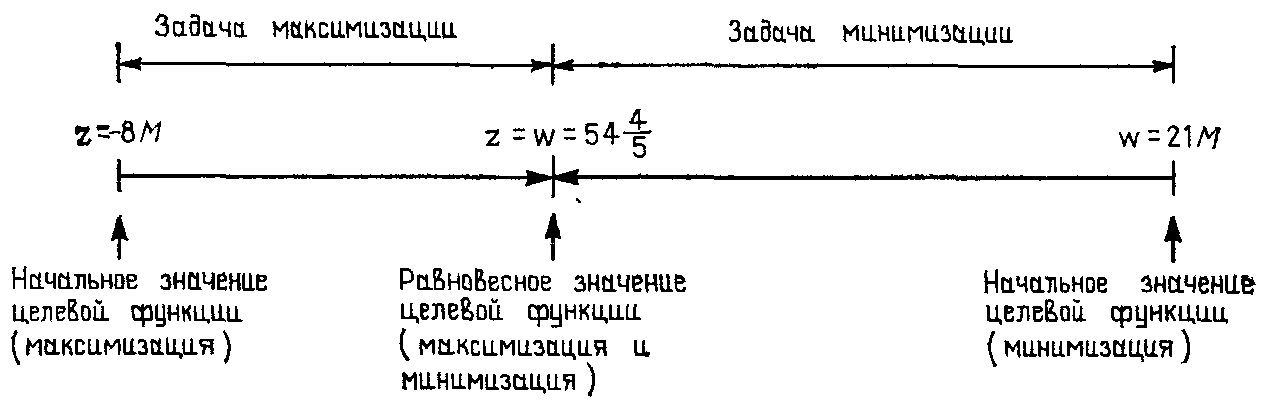
Рис. 4.1.

в любом допустимом решении задачи минимизации всегда является верхним пределом значений целевой функции в любом допустимом решении соответствующей задачи максимизации. Из этого условия следует, что процессы максимизации и минимизации сходятся в некоторой «точке равновесия», после достижения которой целевые функции задач улучшить невозможно. Такая точка достигается при равенстве значений целевых функций обеих задач и соответствует их оптимальным решениям.

Применительно к любой паре прямой и двойственной задач полученные результаты можно обобщить следующим образом.

1. Для любой пары допустимых решений прямой и двойственной задач

Определение. Матрица порядка (mxп) — прямоугольная таблица чисел с количеством строк, равным т, и количеством столбцов, равным п. Вектор-строка размерности n — матрица порядка (1хn), а вектор-столбец размерности т—матрица порядка (mx1). Таким образом, матрица порядка (mхn) состоит из т вектор-строк размерности п и п вектор-столбцов размерности т. Например, матрица

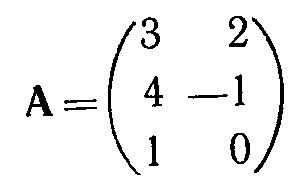
имеет порядок (3х2). Она состоит из двух вектор-столбцов

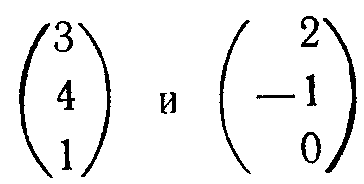
размерности 3 и трех вектор-строк (3, 2), (4, —1) и (1, 0) размерности 2.

Операция умножения вектор-строки на

матрицу. Для заданных вектор-столбца V и матрицы А произведение VxA определено тогда и только тогда, когда размерность V равна числу строк А. Таким образом, если

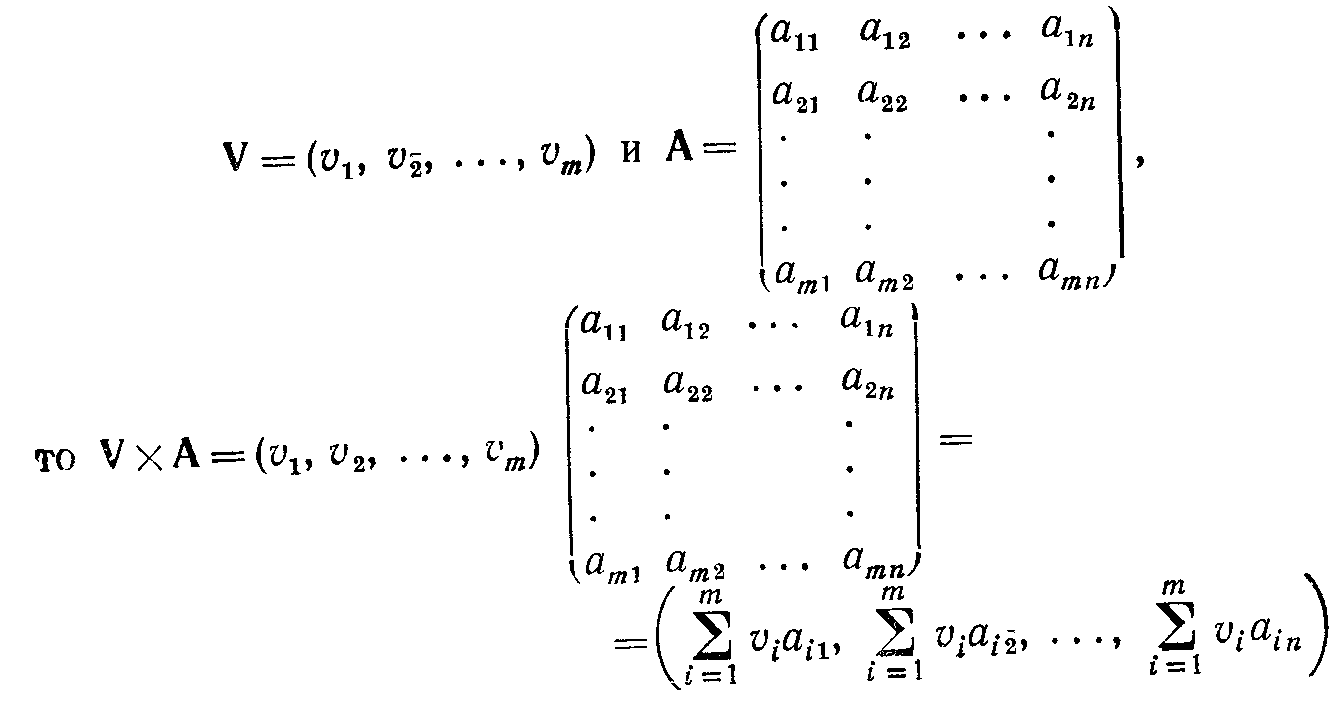
В результате получается вектор-строка размерности n. Данное определение иллюстрирует следующий численный пример:

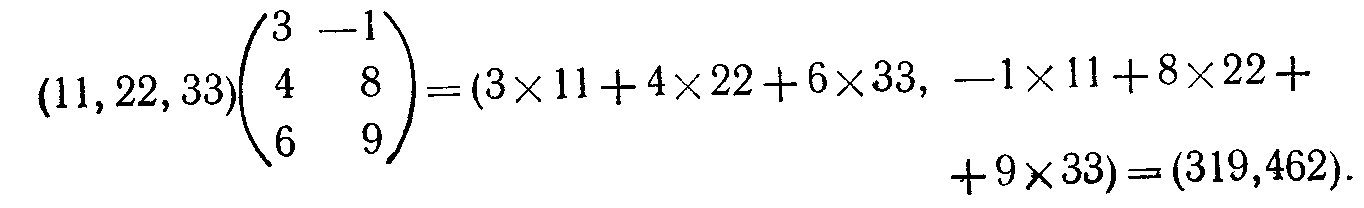
Операция умножения матрицы на вектор-столбец. Произведение АхР матрицы А на вектор-столбец Р определено только в том случае, когда количество столбцов А равно размерности Р. Таким образом, если

то для определенной выше матрицы А

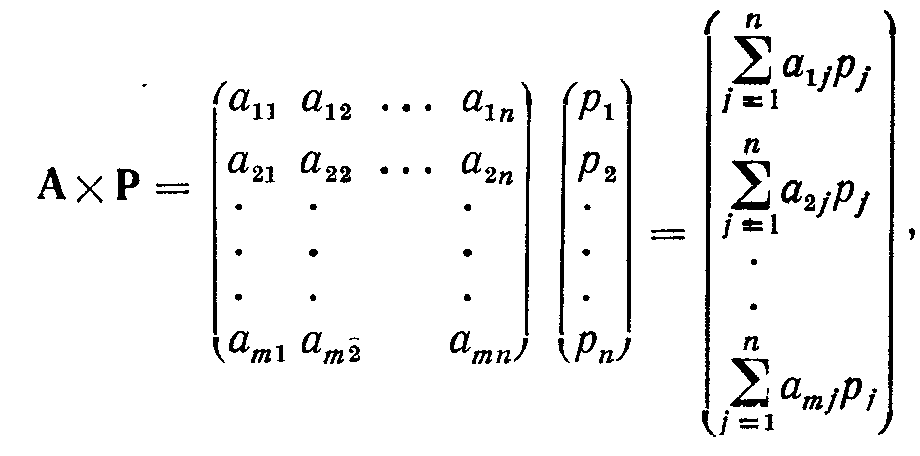
т. е. в результате получается вектор-столбец размерности т. Данное определение можно проиллюстрировать следующим численным примером:

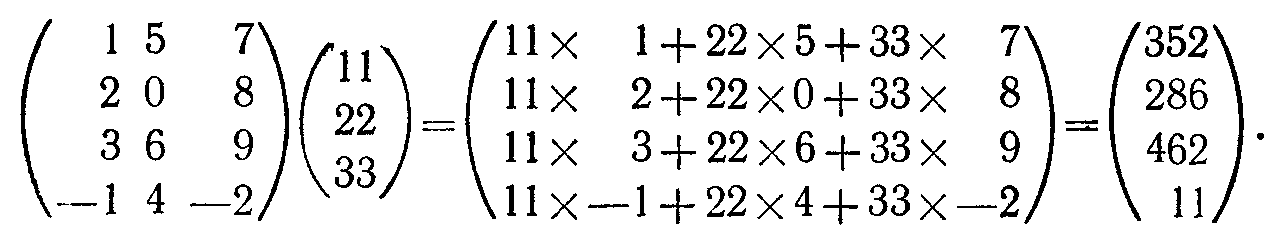
Вычислительные процедуры, основанные на соотношениях двойственности

В вычислительных схемах, использующих взаимосвязь прямой и двойственной задач, существенное значение имеет размещение элементов исходной симплекс-таблицы (гл. 3). Особенность их размещения заключается в том, что т переменным начального базиса всегда отводятся последние т столбцов левой части симплекс-таблицы. Кроме того, соответствующая часть таблицы, содержащая коэффициенты ограничений, ассоциированных с этими переменными, представляет собой единичную матрицу.

Такое расположение элементов симплекс-таблицы позволяет извлечь из нее важную информацию. На рис. 4.2 представлено схематическое изображение симплекс-таблицы, соответствующей любой итерации. Верхняя строка соответствует z-уравнению, а столбцы составлены из коэффициентов, фигурирующих в ограничениях при соответствующих переменных. Матрица, расположенная под начальными базисными переменными, называется обратной матрицей, и ее положение в таблице всегда должно быть таким, как показано на рис. 4.2.

Если обратная матрица задана, то, используя эту матрицу и

коэффициенты исходной модели, можно определить все остальные

Рис. 4.2.

элементы симплекс-таблицы. Чем определяется интерес к вычислениям такого рода? Напомним, что цель анализа модели на чувствительность заключается в том, чтобы выяснить, влияют ли изменения коэффициентов исходной модели на оптимальность или допустимость полученного оптимального решения. Это можно установить, используя соответствующую обратную матрицу и «новые» (измененные) коэффициенты исходной модели для вычисления новых значений остальных элементов симплекс-таблицы.

Вычисления, связанные с определением новых значений элементов симплекс-таблицы, можно разделить на два типа (см. рис. 4.2):

1) вычисления столбцов коэффициентов ограничений и 2) вычисления элементов строки, соответствующей уравнению целевой функции. Вычислительные процедуры первого типа выполняются без использования соотношений двойственности, тогда как вычисления второго типа основаны именно на учете взаимосвязи между решениями прямой и двойственной задач.

Процесс соответствующих вычислений рассмотрим на примере пары прямой и двойственно

й задач, для которых в табл. 4.3 и 4.4 (подразд. 4.2.1) приведены результаты последовательных симплекс-итераций. Для большей наглядности описания вычислительных процедур прямая задача представлена в стандартной форме. Причина включения в прямую задачу искусственной переменной R и соответствующего ей (избыточного) ограничения двойственной задачи будет указана ниже.

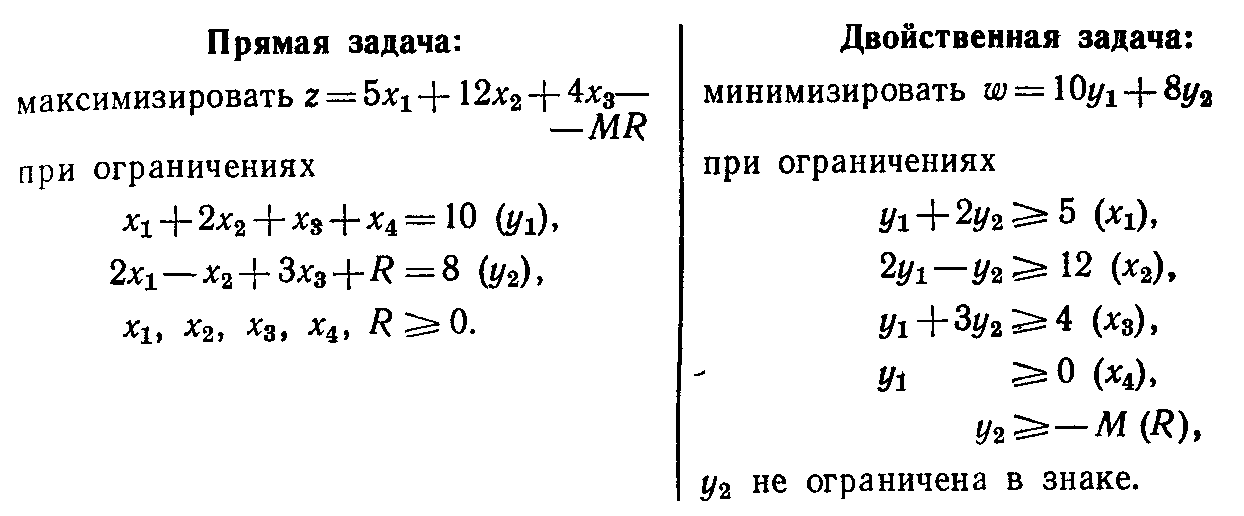
Вычисление столбцов коэффициентов ограничений

На любой симплекс итерации (как для прямой, так и для двойственной задач) столбцы левой или правой части ограничений вычисляются следующим образом:

Чтобы проиллюстрировать использование этого соотношения, рассмотрим сформулированную выше прямую задачу. Начальными базисными переменными являются Х₃ и R. В табл. 4.3 обратная матрица, соответствующая каждой из итераций, заштрихована. Рассмотрим итерацию 1 и соответствующий ей столбец коэффициентов ограничений при переменной х₁ (x₁-столбец):

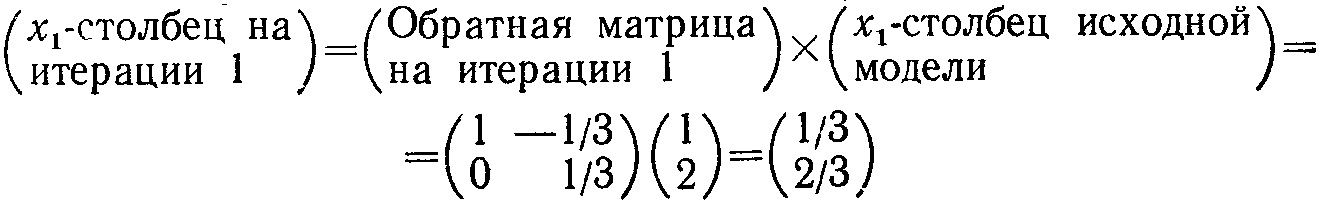
Эти значения коэффициентов совпадают с данными табл. 4.3 для итерации 1.

Рассмотрим теперь итерацию 2 и соответствующий ей столбец коэффициентов в правых частях ограничений:

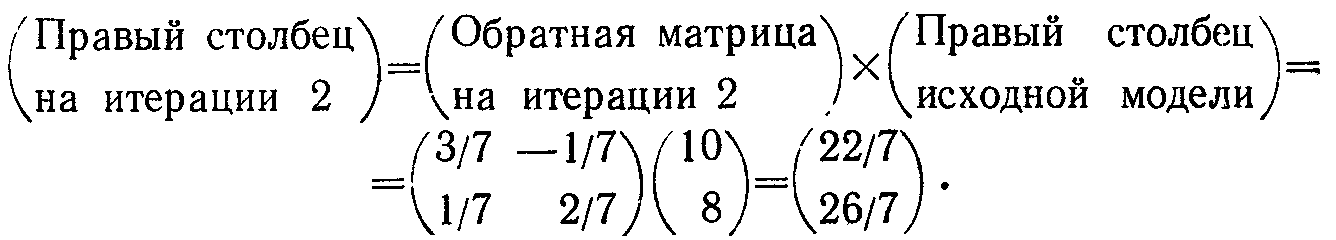
Упражнение 4.2.3. Проверьте справедливость сформулированных выше соотношений на примерах вычисления следующих элементов симплекс-таблиц:

(а) правого столбца на итерации 1 в табл. 4.3;

(б) x₂-столбца на итерации 2 в табл. 4.3;

(в) правого столбца на итерации 3 в табл. 4.3;

(г) у₄ -столбца на заключительной итерации в табл. 4.4;

(д) правого столбца на заключительной итерации в табл. 4,4,

Вычисление элементов строки, соответствующей уравнению целевом функции

На любой итерации элементы строки целевой функции прямой

задачи определяются из соотношения

Применяя это соотношение к рассматриваемой паре задач, получим следующие уравнения (см. ограничения двойственной задачи):

Для нахождения численных значений этих коэффициентов необходимо иметь численные значения двойственных переменных y₁ и y₂. Так как z-коэффициенты для различных итераций не одинаковы, следует ожидать, что и значения переменных y₁ и y₂ будут меняться от итерации к итерации. Значения двойственных переменных на любой итерации определяются из следующего соотношения:

Исходные коэффициенты целевой функции при базисных переменных прямой задачи образуют вектор-строку, элементы которой располагаются в той же последовательности, что и базисные переменные, фигурирующие в соответствующем столбце симплекс-таблицы на данной итерации. Так, в соответствии с табл. 4.3 последовательность вектор-строк, соответствующих приведенному выше соотношению, будет выглядеть следующим образом (б каждом случае обратите снимание на последовательность компонент векторов):

Упражнение 4.2.4. Определите вектор-строку коэффициентов целевой функции при базисных переменных на заключительной итерации в табл. 4.4.

Проиллюстрируем использование приведенного выше соотношения на примере вычисления коэффициентов z-уравнения для итерации 3 (заключительной) табл. 4.3:

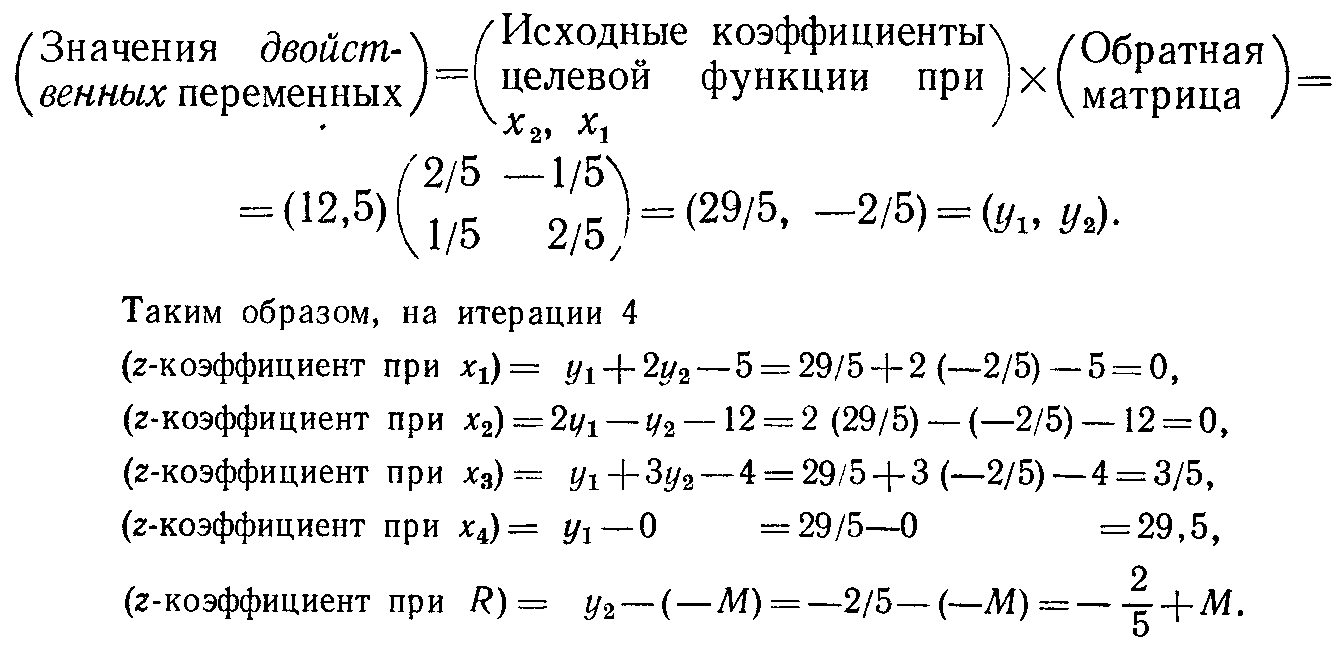
Можно заметить, что двойственные оценки, соответствующие заключительной симплекс-итерации, определяют оптимальное решение двойственной задачи (см. подразд. 4.2.1). Применительно к любой итерации двойственные оценки иногда называют симплекс-множителями. Таким образом, симплекс-множители на заключительной итерации являются оптимальными двойственными оценками.

Выводы относительно вычислений, основанных на соотношениях двойственности

На любой итерации вычисления, основанные на соотношениях двойственности, включают три этапа:

1. Вычисление элементов каждого столбца ограничений путем умножения справа обратной матрицы, соответствующей данной итерации, на исходный вектор-столбец.

2. Получение двойственных оценок, или симплекс-множителей, путем умножения слева обратной матрицы, соответствующей данной итерации, на вектор-строку исходных коэффициентов целевой

функции прямой задачи при переменных, входящих в текущий базис.

3. Вычисление элементов (левой части) z-уравнения как разностей между левыми и правыми частями соответствующих двойственных ограничений.

Практический опыт показывает, что лучший способ усвоения материала, относящегося к «технике» вычислений, основанных на соотношениях двойственности, состоит в следующем. Выберите одну из задач ЛП, сформулированных и решенных в данной главе или гл. 3, и выделите обратную матрицу, соответствующую какой-либо из симплекс-итераций. Затем отложите книгу в сторону и попытайтесь «воспроизвести» все элементы симплекс-таблицы, используя обратную матрицу и исходные условия задачи. В результате должна быть, конечно, получена таблица, тождественная приведенной в книге. Такое упражнение весьма полезно для приобретения навыков соответствующих вычислений.

Два последующих раздела данной главы посвящены экономической интерпретации двойственности и новому методу решения задач ЛП, называемому двойственным симплекс-методом. Переход к изложению этих вопросов в должной степени подготовлен материалом, представленным в настоящем разделе. Экономическая интерпретация двойственности и двойственный симплекс-метод непосредственно используются при анализе моделей на чувствительность.