Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский государственный университет геодезии и картографии

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Маслов А.В., Гордеев А.В., Батраков Ю.Г. - Геодезия

.pdf

Скачиваний:

4639

Добавлен:

10.03.2016

Размер:

6.16 Mб

Скачать

☆

<<< < Предыдущая 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 5758 / 6058 59 60 > Следующая >>>

Допустимая невязка в этом условии	1:11900
Наибольшая поправка:
в измеренную линию, м	0
измеренное направление	2²
измеренный дирекционный угол	0
Средняя квадратическая ошибка единицы веса
(измеренного направления):
заданная	2,0
из уравнивания	1,7
Число определенных пунктов	5

Уравнивание выполнено строгим параметрическим методом по направлениям.

Ведомость измеренных и уравненных значений элементов се˝ти

	Измеренные направления
Q—O	0°00¢00²	2²	0¢00²	0°0¢00²
—Ð4	58 38 40	2	+2²	58 38 42
—Ð1	310 25 40	2	+2	310 25 42
O—Q	0 00 00	2	0	0 00 00
—Ð1	69 27 45	2	–2	69 27 43
—Ð2	143 13 04	2	–3	143 13 01
—Ð3	212 47 34	2	–1	212 47 33
—Ð4	307 16 21	2	–2	307 16 19
Ð1—O	0 00 00	2	0	0 00 00
—Q	60 58 00	2	–1	60 57 59
—Ð2	310 18 56	2	0	310 18 56
Ð2—Ð3	0 00 00	2	0	0 00 00
—Î	53 35 00	2	+3	53 35 03
—Ð1	110 08 41	2	0	110 08 41
Ð3—Ð4	0 00 00	2	0	0 00 00
—Î	47 32 51	2	0	47 32 51
—Ð2	104 23 15	2	+1	104 23 16
Ð4—Q	0 00 00	2	0	0 00 00
—Î	68 37 35	2	+2	68 37 37
—Ð3	106 35 59	2	+1	106 36 00
	Измеренные дирекционные углы
O—Q	140°47¢28²	0¢02²	0¢00²	140°47¢28²
		Измеренные линии
O—Q	2507,180	0,020	0,000	2507,180

571

Каталог координат и высот пунктов

Î	+9506,489	88°03¢47²	2299,151	Ð4
	+10099,607	140 47 28	2507,180	Q
		210 15 11	2182,814	Ð1
		284 00 29	1994,534	Ð2
		353 35 01	1917,291	Ð3
Ð1	+7620,957	30 15 11	2182,814	Î
	+8999,860	91 13 10	2685,268	Q
		340 34 07	2511,369	Ð2
Ð2	+9989,282	50 25 26	2232,748	Ð3
	+8164,388	104 00 29	1994,534	Î
		160 34 07	2511,369	Ð1
Ð3	+11411,770	126 02 10	3106,551	Ð4
	+9885,344	173 35 01	1917,291	Î
		230 25 26	2232,748	Ð2
Ð4	+9584,202	199 26 10	2142,486	Q
	+12397,445	268 03 47	2299,151	Î
		306 02 10	3106,551	Ð3
Q	+7563,810	19 26 10	2142,486	Ð4
	+11684,520	271 13 10	2685,268	Ð1
		320 47 28	2507,180	Î

Приложение 3

Схема полигонометрического хода и распечатка результат˝ов уравнивания параметрическим способом по программе «Сигма»

Исходные данные


		õ	ó

Â	223°25¢04²	6610000,00	5345000,00
À	223°25¢04²	6606868,48	5342036,82
À		6606868,48	5342036,82
Ñ	296°06¢33²	6612206,89	5345537,58
D	296°06¢33²	6614942,89	5339954,98
D		6614942,89	5339954,98

òβ = 5², òS = 2 ñì

572

Рис. Схема полигонометрического хода

1. Параметры хода, угловые и линейные невязки


					fx	fy	fs
Â—Ñ	5,27	5	8²	24¢	+0,261	–0,436	0,509 1:10400

2. Оценка точности уравненных элементов и координат опред˝еляемых пунктов



		mx	my	M	mS, ìì
1	0,018		0,019	0,027	0,019	3²
2	0,026		0,021	0,034	0,019	3²
2	0,026		0,021	0,034
3	0,028		0,021	0,035	0,019	4²
4	0,018		0,020	0,027	0,019	4²
4	0,018		0,020	0,027
	Технические характеристики сети планового обоснования
	Число измеренных элементов					17
	В том числе:
	направлений					12
	длин линий					5
	Число избыточных измерений					3
	Из них выявлено и проконтролировано невязками
	геометрических условий:
	угловых					1
	координатных					2

573

Наибольшая угловая невязка полигона	8²
Допустимая невязка на этот полигон	24²
Наибольшая координатная невязка полигона:
абсолютная, м	0,509
относительная	1:10400
Наибольшая поправка:
в измеренную линию, м	0,044
в измеренное направление	12²
Средняя квадратическая ошибка единицы веса	3,5²
(измеренного направления) заданная
Число определяемых пунктов	4

3. Ведомость измеренных и уравненных значений элементов с˝ети

		Направления
Â—À	0°00¢00²	4²	0²	0°00¢00²
—1	231 36 01	4	+3	231 36 24
Ñ—D	0 00 00	4	0	0 00 00
—4	137 12 10	4	+2	137 12 12
1—Â	0 00 00	4	0	0 00 00
—2	129 06 38	4	+13	129 06 51
2—1	0 00 00	4	0	0 00 00
—3	149 58 01	4	+2	149 58 03
3—2	0 00 00	4	0	0 00 00
—4	127 57 01	4	–13	127 56 48
4—3	0 00 00	4	0	0 00 00
—Ñ	111 15 50	4	–15	111 15 35
		Линии
Â—1	1169,680	0,020 ì	+0,034	1169,714
1—2	862,760	0,020	–0,002	862,758
2—3	1294,770	0,020	–0,024	1294,746
3—4	922,350	0,020	–0,044	922,306
4—Ñ	1019,830	0,020	–0,020	1019,810
	4. Каталог координат пунктов


1	+6609897,551	44°08¢20²	862,758	2
	+5346165,218	275 01 29	1169,714	Â
2	+6610516,714	14 06 22	1294,746	3
	+5346766,043	224 08 20	862,758	1
3	+6611772,418	194 06 22	1294,746	2
	+5347081,599	322 03 10	922,306	4

574

				Продолжение


4	+6612499,727	142 03 10	922,306	3
	+5346514,441	253 18 46	1019,810	Ñ
À	+6606868,480	43 25 04	4311,247	Â
	+5342036,820
Â	+6610000,000	95 01 29	1169,714	1
	+5345000,000	223 25 04	4311,247	À
Ñ	+6612206,890	73 18 46	1019,810	4
	+5345537,580	296 06 33	6217,002		D
D	+6614942,890	116 06 33	6217,002	Ñ
	+5339954,980

Приложение 4

Вычисление средних квадратических погрешностей положен˝ия определяемых пунктов I, II, III геодезического четырехугольника трилатерац˝ии при уравнивании коррелатным способом

Пункт I

F = xI = xA + S4cos αA—I;

β +

= (

)

= = =

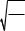F = yI = yA + S4sin αA—I;

575

β =

β +

Пункт II

F = S3;

∂

Êî í ò ð î ë ü

== =

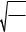576

Пункт III

F = xIII = xA + S1cos αA—III;

β +

F = yIII = yA + S1sin αA—III;

β + α

β =

577

Приложение 5

Распечатка результатов уравнивания геодезического четы˝рехугольника трилатерации параметрическим способом по программе «Си˝гма»

5.1. Оценка точности уравненных элементов и координат опред˝еляемых пунктов


				òS, ì
	òõ	òó	Ì	òS, ì
I	0,088	0,077	0,118	0,085	11²
II	0,029	0,065	0,071	0,085	11²
II	0,029	0,065	0,071
III	0,078	0,088	0,118

2. Ведомость измеренных и уравненных значений элементов с˝ети

		Дирекционные углы
A—II	66°00¢00²	7²	0¢00²	66°00¢00²
		Линии
A—I	3447,710	0,085	–0,038 ì	3447,672
I—II	2118,990	0,085	–0,038	2118,952
II—III	3441,280	0,085	–0,027	3441,253
III—A	3789,500	0,085	–0,019	3789,481
A—II	5040,720	0,085	+0,050	5040,770
I—III	3756,210	0,085	+0,033	3756,243

3. Каталог координат пунктов

À	+10000,000	46°42¢24²	3447,672	I
	+10000,000	66 00 00	5040,770	II
		109 01 44	3789,481	III
I	+12364,180	98 31 10	2118,952	II
	+12509,401	163 24 07	3756,243	III
		226 42 24	3447,672	À
II	+12050,266	197 17 12	3441,253	III
	+14604,972	246 00 00	5040,770	À
		278 31 10	2118,952	I
III	+8764,452	17 17 12	3441,253	II
	+13582,400	289 01 44	3789,481	À
		343 24 07	3756,243	I

578

Приложение 6

Методика спутниковых наблюдений и обработки базовых лин˝ий

Обработку результатов спутниковых наблюдений выполняют˝ с помощью пакета программ, входящего в комплект приемника, включающег˝о три основных модуля: обработки базовых линий, уравнивания сетей и вспо˝могательного модуля планирования наблюдений, результаты работы которого мож˝но выводить на принтер.

Модуль обработки базовых линий обеспечивает вычисление˝ приращений координат с относительной ошибкой 1 · 10–6 и меньше в зависимости от точности эфемерид.

Обработку фазовых измерений выполняют в три этапа:

решение по третьим разностям дает первую оценку компонен˝тов базовой линии и позволяет зафиксировать срывы цикла; приращения коо˝рдинат, полученные на этом этапе, используются в дальнейших вычислениях;˝

плавающее решение позволяет обрабатывать коррелированн˝ые вторые разности фаз. Срывы циклов, которые не были разрешены по третьим˝ разностям, разрешаются по дополнительным дугам орбит спутников; это реш˝ение дает компоненты базовых линий и плавающие неоднозначности;

фиксированное решение по вторым разностям позволяет с по˝мощью алгоритма временнó й оптимизации разрешить оптимальную фазовую неоднознач˝ность из плавающего решения по методу наименьших квадратов. Для пр˝оверки правильности разрешения неоднозначности используются статисти˝ческие тестыχ-квадрат и Фишера с доверительной вероятностью 95 и 99 % соответствен˝но.

Процедура наблюдений и обработки базовых линий рассмотр˝ена на примере эталонной линейно-угловой сети геодезического полигона˝ (рис.).

Измерения выполнены по классической методике с установк˝ой одного из приемников на пункте сети, выбранном в качестве базового ˝и включенного на весь день работы с интервалом записи 10 с, и перемещением др˝угого (мобильного)

Рис. Схема базовых линий (исходные пункты В20, В360)

579

приемника от одного пункта к другому. Время записи ограни˝чено 15 мин сознательно в целях исследования точностных возможностей ком˝плекта за этот сравнительно короткий промежуток времени.

В первый день работы в качестве базового был выбран пункт˝ В20, во второй — В360 (см. рис.) на открытых участках базиса. Обмен данными с ком˝пьютером, контроль ежедневных результатов проводили вечером; общу˝ю обработку, уравнивание и трансформацию координат пунктов сети — в конце п˝олевых работ.

Фрагмент файла с результатом обработки наблюдений базов˝ой линии В20—В624

		Пункт В20 (базовый)
Геоцентрические коорди-			2 821 260,612		2 211 019,720		5 258 137,912
íàòû X, Y, Z, ì
Смещение координат и высота			0			0		1,453
приемника N, E, H, м
Неделя, день года, дата			1016			184		3 èþëÿ 2003
Начало, конец интервала			539 600,0		565 560,0			10,0
(в секундах с начала недели)
Номер спутника PRN	3	6	7	8	9	10	13	14	17
Число наблюдений	1710	911	126	786	599	581	449	383	1631
за все время
Номер спутника PRN	21	22	23	24	25	26	29	30	31
Число наблюдений	1956	1211	1920	41	413	1019 1296		251	1562
за все время
			Пункт В624
Геоцентрические коорди-			2 820 771,001		2 211 440,786		5 258 142,364
íàòû X, Y, Z, ì
Смещение координат и высота			0			0		1,496
приемника N, E, H, м
Неделя, день года, дата			1016			184		3 èþëÿ 2003
Начало, конец интервала			548 170,0		549 110,0			10,0
(в секундах с начала недели)
Номер спутника PRN		3	6	17	21	22	23	26	31
Число наблюдений		95	43	95	95	95	95	95	71
за все время

1. Сводная характеристика фазовых наблюдений с интервалом˝ 10 с

3	95	45°	51°	41	48
6	43	10	13	32	39
17	95	59	67	41	49
21	95	26	34	40	46
22	95	25	31	39	45
23	95	59	65	42	49
26	95	26	26	38	43

580

<<< < Предыдущая 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 5758 / 6058 59 60 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
18.08.2019180.74 Кб28лекция2.doc
#
18.08.2019169.47 Кб21лекция5.doc
#
01.05.2025744.96 Кб3Лк1-2(установочная)_и_тесты_к_зачету!.doc
#
01.07.2025223.23 Кб1МАКАРЕНКА.doc
#
01.04.2025848.38 Кб2манулья шпаргалочка.docx
#
10.03.20166.16 Mб4639Маслов А.В., Гордеев А.В., Батраков Ю.Г. - Геодезия.pdf
#
02.05.2015116.54 Кб112МАСТЕР КЛАСС ПО КОНФЛИКТОЛОГИИ.docx
#
01.03.2025243.71 Кб2Матан. Часть 2.doc
#
01.03.2025274.94 Кб1Матан. Часть 3.doc
#
01.07.2025406.37 Кб0Математика(примеры).docx
#
01.07.2025682.5 Кб0Математика(теория).docx