
Маслов А.В., Гордеев А.В., Батраков Ю.Г. - Геодезия
.pdf
длину исходной стороны, выполняют предварительное решен˝ие
треугольников (табл. 14.2); используя теорему синусов
àsin A = bsin B = csin C = D, |
(14.1) |
находят приближенные длины сторон, необходимые для вычис˝ления поправок за центрировку и редукцию.
14.2. Предварительное решение треугольников
|
|
D1 = 2870 |
|
|
|
I |
Выселки (Ð1) |
2(Â1) |
60°58′ |
0,874 |
2510 |
|
Ольгово (Î) |
3(Ñ1) |
69 28 |
0,936 |
2690 |
|
Архипово (Q) |
1(À1) |
49 34 |
0,761 |
2180 |
|
|
|
180°00′ |
|
|
|
|
D2 = 2610 |
|
|
|
II |
Ступино (Ð2) |
5(Â2) |
56°34′ |
0,834 |
2180 |
|
Ольгово (Î) |
6(Ñ2) |
73 45 |
0,960 |
2510 |
|
Выселки (Ð1) |
4(À2) |
49 41 |
0,762 |
1990 |
|
|
|
180°00′ |
|
|
III |
… |
… |
… |
… |
… |
Общие стороны смежных треугольников называют связующими (OQ, OP1, OP2 и т. д.), остальные стороны (Q1Ð1, ÐÐ2 è ò. ä.) — промежуточными. Углы, противолежащие связующим сторонам, на-
зывают связующими углами, остальные — промежуточными. Связующие углы обозначим AR è BR в порядке их следования,
ãäå R — номер треугольника (R = 1, 2, …, N), а промежуточные — CR. Противолежащие этим углам стороны обозначим соответств˝енно aR, bR, cR. Таким образом, в каждом треугольнике исходная сторона будет обозначена b, а в предыдущем треугольнике она же обозначена à. В практике геодезического производства углы обычно обозначают арабскими цифрами, как на рисунке 14.2.
В каждом треугольнике, начиная с первого, по стороне bR è óãëó BR находят отношение DR = bR/sin BR, которое записывают над значениями синусов углов треугольника. Две другие сто˝роны треугольника вычисляют по формулам
aR = DRsin AR è ñR = DRsin ÑR.
Контролем решения треугольников является сходимость вы˝-
численного значения длины стороны aN с исходным ее значе-
íèåì b1.
Для приведения направлений к центрам пунктов определяют˝ поправки за центрировку и редукцию. Вывод формул этих поп˝равок рассмотрим ниже.
411
|
|
|
|
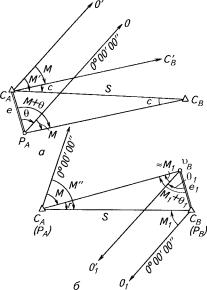
Пусть Ñ4 (ñì. ðèñ. 14.2, à) — |
||
|
|
|
|
проекция |
на горизонтальную |
|
|
|
|
|
плоскость |
центра пункта À; |
|
|
|
|
|
ÐÀ — проекция |
вертикальной |
|
|
|
|
|
оси прибора (теодолита), уста- |
||
|
|
|
|
новленного на том же пункте; |
||
|
|
|
|
ÑÂ — проекция центра пункта |
||
|
|
|
|
Â; å, q — линейный и угловой |
||
|
|
|
|
элементы центрировки. |
||
|
|
|
|
Начальное направление ÐÀÎ, |
||
|
|
|
|
т. е. направление, для которо- |
||
|
|
|
|
го определен угловой элемент |
||
|
|
|
|
центрировки q, является одно- |
||
|
|
|
|
временно нулевым (0°00¢00²). |
||
|
|
|
|
Обозначим измеренное направ- |
||
|
|
|
|
ление на пункт Â буквой Ì. |
||
|
|
|
|
 û â î ä ô î ð ì ó ë û ï î - |
||
|
|
|
|
ï ð à â ê è ç à ö å í ò ð è ð î â - |
||
|
|
|
|
к у. Представим, что теодолит |
||
|
|
|
|
стоит точно над центром пун- |
||
|
|
|
|
кта, а нулевой диаметр гори- |
||
|
|
|
|
зонтального круга параллелен |
||
Рис. 14.2. Схемы для вывода формул по- |
его положению, которое он за- |
|||||
нимал при наблюдении на- |
||||||
правок за центрировку (à) и редукцию (á) |
правлений. При таком усло- |
|||||
|
|
|
|
|||
|
|
|
|
вии нулевой отсчет будет соот- |
||
|
|
|
|
ветствовать прямой ÑÀ΢, ïà- |
||
раллельной ÐÀÎ, а отсчет на пункт  будет Ì¢. |
|
|||||
Проведем |
прямую |
¢ |
параллельную |
ÐÀÑÂ. Тогда |
||
Ð ¢ |
¢ = |
à Ð ¢ |
= — поправка за центрировку в изме- |
|||
ренное направление Ì. Приведенное к центру пункта направление
Ì¢ = Ì + ñ.
Согласно теореме о внутренних накрест лежащих углах при п˝а-
раллельных прямых, пересеченных третьей прямой,
= Ð ¢ |
= Ð |
Из решения треугольника ÑÀÑÂÐÀ по теореме синусов имеем
sin C = esin (M + q)/S.
Отсюда с учетом того, что угол ñ ìàë
= |
+ q |
r¢¢ |
|
412

Òàê êàê å и r — постоянные величины, то обозначим k = er. Тогда рабочая формула для вычисления поправки за центрировку
¢¢ = + q (14.2)
В ы в о д ф о р м у л ы п о п р а в к и з а р е д у к ц и ю. Пусть ÑÀ, Ñ è u (ðèñ. 14.2, á) — проекции на горизонтальную
плоскость соответственно центров пунктов À, Â и оси визирного
цилиндра на пункте Â.
Как видно из рисунка 14.2, á, при отсутствии смещения оси визирного цилиндра относительно центра пункта Â приведенное
значение направления с пункта À на пункт Â было бы равно
̲ = Ì + r,
ãäå Ì — измеренное направление на пункт Â; r — поправка за редукцию.
Для вывода формулы поправки r проведем прямую u ¢ па-
раллельную начальному (нулевому) направлению. Тогда
Ð u ¢ » Ð =
ãäå Ì1 — измеренное направление с пункта Â на пункт À.
Из решения треугольника ÑÀÑÂu по теореме синусов найдем
=+ q
Отсюда с учетом того, что угол r ìàë,
¢¢ = + q r¢¢ (14.3)
Так же, как и при выводе поправки за центрировку, обозначим˝
å1r = k1.
Тогда рабочая формула вычисления поправки за редукцию будет
¢¢ = |
|
+ q |
|
Пример вычисления поправок ñ по формуле (14.2) и r по формуле (14.3) приведен в таблице 14.3.
413
14.3. Вычисление поправок за центрировку и редукцию
Пункт Архипово |
å = 0,030 ì; å1 = 0,035 ì; |
q = 175°; q1 = 30°; íà |
пункт Выселки |
|||
k = er² = 6180; k1 = e1r = 7210 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ì |
0°00¢ |
|
49°34¢ |
|
108°13¢ |
|
S |
2690 |
|
2510 |
|
2140 |
|
q |
175° |
|
175° |
|
175° |
|
Ì + q |
175°00¢ |
|
224°34¢ |
|
283°13¢ |
|
sin (M + q) |
+0,259 |
|
–0,702 |
–0,974 |
||
k/S |
2,30 |
|
2,46 |
|
2,89 |
|
ñ |
+0,6² |
|
–1,7² |
–2,8² |
||
q1 |
30° |
|
30° |
|
30° |
|
Ì + q1 |
30°00¢ |
|
79°34¢ |
|
138°13¢ |
|
sin (M + q1) |
+0,500 |
|
+0,983 |
|
+0,666 |
|
k1/S |
2,68 |
|
2,87 |
|
3,37 |
|
r |
+1,3² |
|
+2,8² |
|
+2,2² |
|
Все измеренные направления приводят к центрам пунктов (табл. 14.4) путем введения поправок за центрировку и редукци˝ю по формуле
Ì¢ = Ì + ñ + r.
При этом для каждого направления берут свои значения ñ è r.
14.4. Вычисление приведенных направлений
|
Направ- |
Измерен- |
|
Поправка |
|
|
(c + r)i |
– |
Приведенное |
|
|
íîå íà- |
|
|
|
|
|
||||
Пункт |
ление |
c |
|
r |
(c + r) |
|
||||
|
на пункт |
правление |
|
i |
– (c + r)0 |
направление |
||||
|
Ìi |
i |
|
i |
|
|
|
¢ |
||
|
|
|
|
|
|
|
|
|
||
|
Выселки |
0°00¢00² |
+0,6² |
+2,1² |
+2,7² |
0,0² |
|
0°00¢00² |
||
Архипово Ольгово |
49 34 24 |
–1,7 |
+0,2 |
–1,5 |
|
–4,2 |
|
49 34 20 |
||
|
Ермолино |
108 13 09 |
–2,8 |
|
–0,6 |
–3,4 |
|
–6,1 |
|
108 13 03 |
Для того чтобы начальное направление оставалось нулевым˝, т. е. 0°00¢00², все поправки за центрировку и редукцию до их вве-
дения в направления преобразуют по формуле
+ |
= + |
+ |
(14.4) |
ãäå i = 1, 2, …, ï — номер направления.
После введения поправок получают направления, приведенн˝ые к центрам пунктов. Так как преобразованная поправка в нач˝аль-
ное направление равна нулю, то и приведенное значение нач˝ального направления будет 0°00¢00².
414

При вычислении |
поправок |
|
(ñ + r)i следует иметь в виду, что по- |
|
|
правки за центрировку ñi берут из |
|
|
вычислений на исходном пункте, |
|
|
где проведены наблюдения, а по- |
|
|
правку за редукцию ri |
— из вычис- |
|
лений на том пункте, на который |
|
|
наблюдали. |
|
|
Приведенные направления вы- |
|
|
писывают на схему сети (рис. 14.3). |
Рис. 14.3. Приведенные направле- |
|
Углы вычисляют как разности при- |
ния и углы на п. Архипово |
|
веденных направлений. После это-
го в треугольниках подсчитывают угловые невязки. Допусти˝мые
невязки определяют по формуле
= β  (14.5)
(14.5)
ãäå òβ — средняя квадратическая погрешность измерения угла.
Согласно инструкции для триангуляции 2-го разряда òβ = 10².
Тогда
= |
¢¢ = ¢¢ |
(14.6) |
По невязкам треугольников определяют среднюю квадратич˝ес-
кую погрешность измерения угла, применяя формулу
|
β = |
|
|
|
(14.7) |
|
|
|
|
|
|||
ãäå N — число треугольников в сети. |
|
|
|
|
||
Ï ð è ì å ð. Ïî |
невязкам треугольников |
w1 = +10², w2 = –12², w3 = +21², |
||||
v4 = –9², w5 = +24² |
вычислить среднюю квадратическую погрешность измере- |
|||||
íèÿ óãëà. |
|
|
|
|
|
|
|
β = |
|
|
= |
|
¢¢ |
|
|
|
|
|||
14.3. ОКОНЧАТЕЛЬНЫЕ ВЫЧИСЛЕНИЯ
Окончательные вычисления включают: уравнивание геодези˝-
ческой сети; вычисление координат пунктов и составление к˝аталога координат. Задача уравнивания сети состоит в определ˝ении
таких поправок к измененным углам, чтобы исправленные зна˝че- ния углов удовлетворяли всем условиям, возникающим в этой˝ сети.
415
Каждой избыточной величине в геодезической сети соответ˝-
ствует одно независимое от других условие, а r избыточным вели- чинам — r независимых условий.
Некоторые условия возникают из-за наличия в сети исходных˝ элементов. Геодезическая сеть, в которой имеется хотя бы о˝дно условие, связанное с наличием в ней исходных элементов, яв˝ляется несвободной.
Исходные элементы сети обычно принимают за точные, они не˝ подлежат изменению. В действительности они содержат погр˝еш-
ности, которыми иногда нельзя пренебрегать, так как они мо˝гут понизить точность вновь создаваемой сети. Каждому услови˝ю отвечает одно условное уравнение поправок.
Существуют строгие и упрощенные способы уравнивания. Строгие способы уравнивания базируются на методе наименьших квадратов. Их применяют в основном при уравнивании государственной геодезической сети, сети сгущения 1-го разряда и о˝пор-
ной межевой сети 1-го класса.
Уравнивание триангуляции 2-го разряда обычно выполняют упрощенным способом как более простым для вычислений. При˝
этом для вывода формул поправок к результатам измерений и˝с- пользуют, с некоторыми ограничениями, один из строгих спо˝собов уравнивания — коррелатный.
У р а в н и в а н и е п о м е т о д у н а и м е н ь ш и х к в а д - р а т о в. Он состоит в определении поправок u1, u2, …, uï к резуль-
татам измерений, удовлетворяющих условию [u2] = min, если измерения равноточны, или [pu2] = min, если измерения неравноточны и характеризуются весами ð1, ð2, ð3, …, ðï.
Значения величин, уравненные по методу наименьших квадра˝- тов, являются в некотором смысле наилучшими по сравнению ˝с
результатами уравнивания другими методами.
К о р р е л а т н ы й с п о с о б у р а в н и в а н и я. Он состоит в следующем. Пусть уравниваемой геодезической сети соо˝тветствует система независимых условных уравнений поправок˝
u |
+ |
u |
+ |
+ |
u |
+ |
= |
ü |
|
u |
+ |
u |
+ |
+ |
u |
+ |
= |
ï |
|
ï |
|
||||||||
|
|
|
|
|
|
|
|
ý |
(14.8) |
|
|
|
|
|
|
|
|
ï |
|
u |
+ |
u |
+ |
+ |
u |
+ |
= |
ï |
|
þ |
|
ãäå b11, b12, …, b1n, …; br1, br2, …, brn — коэффициенты, а w1, w2, …, wr — свободные члены (невязки) уравнений.
Рассмотрим решение задачи по определению поправок для случая равноточных измерений в соответствии с принципом˝ [u2] = min. Эта задача относится к математическому анализу на ус˝-
416
ловный экстремум. Она может быть решена с помощью множите˝-
лей Лагранжа, называемых коррелатами.
Для такого решения составляют функцию Лагранжа
F = [u2] – 2k1([b1u] + w1) – 2k2([b2u] + |
|
+ w2) – … – 2kr[(ru] + wr). |
(14.9) |
Затем функцию исследуют на экстремум, для чего находят ее˝ частные производные и приравнивают их к нулю:
¶ |
= |
u |
= |
ü |
|
||
|
|
ï |
|
||||
|
¶u |
|
|||||
|
|
|
|
ï |
|
||
¶ |
|
|
|
|
|||
= |
u |
= |
ï |
|
|||
|
|
ï |
|
||||
¶u |
(14.10) |
||||||
|
|
|
ý |
||||
|
|
|
|
|
ï |
|
|
¶ |
|
|
|
ï |
|
||
= |
u |
= |
ï |
|
|||
|
|
ï |
|
||||
¶u |
|
||||||
|
|
|
þ |
|
|||
Отсюда
u |
= |
+ |
+ |
+ |
ü |
|
u |
= |
+ |
+ |
+ |
ï |
|
ï |
(14.11) |
|||||
|
|
|
|
|
ý |
|
|
|
|
|
|
ï |
|
u |
= |
+ |
+ |
+ |
ï |
|
þ |
|
Равенства (14.11) называют коррелатными уравнениями поправок.
Подставляя выражения поправок (14.11) в условные уравнения
(14.8), после приведения подобных членов получаем систему ура˝в- нений
+ |
+ |
+ |
+ |
= |
ü |
|
+ |
+ |
+ |
+ |
= |
ï |
|
ï |
(14.12) |
|||||
|
|
|
|
|
ý |
|
|
|
|
|
|
ï |
|
+ |
+ |
+ |
+ |
= |
ï |
|
þ |
|
которую называют системой нормальных уравнений коррелат. Число нормальных уравнений равно числу неизвестных корр˝е-
лат, т. е. матрица из коэффициентов является квадратной.
Квадратичные коэффициенты [b1b1], [b2b2], …, [brbr] располагаются по так называемой главной диагонали определителя си˝сте-
417

мы. Остальные — неквадратичные коэффициенты, расположе˝н-
ные симметрично относительно главной диагонали, равны ме˝жду собой.
Решая систему уравнений (14.11), находят поправки υ1, υ2, …, υï. В том случае, когда в сети имеется только одно условное
уравнение вида
b11υ1 + b12υ2 + … + b1ïυï + w = 0,
ему будет соответствовать одно нормальное уравнение кор˝релат
[b1b1]k + w = 0, |
(14.13) |
||
откуда |
|
|
|
= |
|
|
(14.14) |
|
|
||
Коррелатные уравнения поправок в этом случае будут |
|
||
υ1 = b11k, |
|
||
υ2 = b12k, |
(14.15) |
||
.............. |
|
|
|
υï = b1ïk.
Например, если определяют третий пункт сети по двум пунктам и трем измеренным углам треугольника, вершинами котор˝ого
являются эти три пункта, то поправки в измеренные значени˝я уг-
лов треугольника по изложенному способу получают следую˝щим образом.
Условное уравнение поправок будет
υ1 + υ2 + υ3 + w = 0,
нормальное уравнение коррелат
3k + w = 0.
Отсюда
=
Поправки к измеренным углам в соответствии с формулами (14.15) будут
υ= υ = υ =
ò.е. невязка распределяется с противоположным знаком, по˝ровну на все углы треугольника.
418
Ï à ð à ì å ò ð è ÷ å ñ ê è é ñ ï î ñ î á ó ð à â í è â à í è ÿ. Îí
состоит в следующем. Пусть в геодезической сети имеется t параметров (необходимых неизвестных), подлежащих определени˝ю, точные значения которых обозначим Õ1, Õ2, …, Õt. Для их определения измерено ï элементов сети, точные значения которых L1,
L2, …, Ln.
Уравнивание происходит при ï > t. Разность r = n – t равна чис-
лу избыточных измерений (степеней свободы).
Точные значения элементов сети Li и параметров Õi связаны
математическими зависимостями, называемыми параметрическими уравнениями связи:
L1 = a11X1 + a21X2 + … + a1tXt + a10; |
|
L2 = a21X1 + a22X2 + … + a2tXt + a20; |
(14.16) |
........................................................ |
|
Ln = an1X1 + an2X2 + … + antXt + at0.
В процессе измерений получают значения элементов сети λ1,
λ2, …, λï с весами ð1, ð2, …, ðï. В результате уравнивания находят приближенные, однако близкие к точным значениям параметр˝ов,
величины õ1, õ2, …, õt.
Разность между точным значением измеряемой величины Li è |
|||||
результатом измерения λ1 есть точная поправка |
|
|
|||
|
υ = |
λ |
|
|
(14.17) |
С учетом формулы (14.17) точная поправка будет |
|
||||
υ = |
+ |
+ + |
+ |
λ |
(14.18) |
Заменяя в выражении (14.18) точные значения определяемых параметров Õ1, Õ2, …, Õt их приближенными значениями õ1,
õ2, …, õt, получают параметрические уравнения поправок в виде
υ1 = à11õ1 + à21õ2 + … + àt1õt + a01 – λ1; |
|
υ2 = à12õ1 + à22õ2 + … + àt2õt + a02 – λ2; |
(14.19) |
.............................................................. |
|
υï = à1ïõ1 + à2ïõ2 + … + àtïõt + a0t – λt.
При уравнивании удобнее и точнее вычислять малые поправк˝и dõi вместо õi. Поэтому вводят предварительные значения искомых
параметров так, чтобы = + δ поэтому параметрические
уравнения поправок примут вид
|
|
υ1 = à11δõ1 + à21δõ2 + … + àt1δõt + l1; |
|
|
|
|
υ2 = à12δõ1 + à22δõ2 + … + àt2δõt + l2; |
(14.20) |
|
|
|
.......................................................... |
|
|
|
|
υn = à1nδõ1 + à2nδõ2 + … + àtnδõt + ln, |
|
|
ãäå dõi — поправка к предварительному значению i-го параметра; = |
+ |
+ |
||
+ + |
+ |
λ |
|
|
419

Приближенные значения параметров находят под условием
[pυ2] = min. В связи с этим нормальные уравнения получим в виде
[pa1a1]δx1 + [pa1a2]δx2 + … + [pa1at]δxt + [pa1l] = 0;
[pa1a2]δx1 + [pa2a2]δx2 + … + [pa2at]δxt + [pa2l] = 0; (14.21)
................................................................................
[pa1at]δx1 + [pa2at]δx2 + … + [patat]δxt + [patl] = 0.
Общее число уравнений равно числу неизвестных, т. е. t.
В результате решения системы нормальных уравнений получ˝а-
ют поправки δõ1, δõ2, …, δõt к предварительным значениям неизве-
стных.
Затем по формуле
= + δ |
= |
|
(14.22) |
находят уравненные значения параметров.
Оценка точности по результатам параметрического уравни˝ва-
ния включает определение средних квадратических погреш˝ностей измеренных и уравненных величин, а также их функций. В обще˝м
случае для этого используют формулу
= μ = μ |
(14.23) |
ãäå μ — средняя квадратическая погрешность единицы веса.
Правая форма записи погрешности (14.23) предпочтительнее, так как обычно в процессе уравнивания вычисляют не сам ве˝с, а его обратную величину — так называемый обратный вес.
Таким образом, для оценки точности некоторой величины не-˝
обходимо по результатам уравнивания определить μ è 1/ði.
При уравнивании различают априорные è апостериорные значе- ния средней квадратической погрешности. Априорное значе˝ние μ0 этой погрешности устанавливают до уравнивания при вычислении весов измеренных величин по предполагаемым погрешно˝- стям отдельных измерений.
Апостериорное значение μ получают по результатам уравнивания в соответствии с формулой
μ = |
υ |
(14.24) |
|
Обычно значения μ0 è μ численно различаются. Это происходит из-за неточности назначения численных значений погре˝шностей измерений при вычислении их весов перед уравнивание˝м,
420
