Маслов А.В., Гордеев А.В., Батраков Ю.Г. - Геодезия

Вначале с чертежа сети выписывают в координатную ведомос˝ть

(см. табл. 18.3) по каждому ходу отдельно исходные данные — д˝и-

рекционные углы и координаты, измеренные значения углов и˝ горизонтальные проложения сторон. Подсчитывают по ходам су˝м-

мы измеренных углов. Затем вычисляют по каждому ходу знач˝е-

ния дирекционного угла αi узловой линии QR и подсчитывают

число углов ïi, а результаты записывают в таблицу 18.1.

Находят невязки по ходам 1 + 2 è 2 + 3, в которых число углов меньше, чем в ходе 1 + 3, и сравнивают их с соответствующими допусками.

После проверки допустимости невязок приступают к уравни˝-

ванию. Выбрав приближенное значение α0, находят остатки εi = αi – α0; вычисляют веса ði = k/ni значений αi; подсчитывают [p], ðiεi è [pε]. Затем находят окончательное значение дирекционного угла α узловой линии QR и угловые невязки по ходам. Конт-

роль вычислений проводят по формуле [pfβ] = 0.

Окончательное значение дирекционного угла узловой лини˝и

записывают в координатную ведомость (см. табл. 18.3). По каждо˝- му ходу подсчитывают теоретическую сумму углов и вычисля˝ют

(вторично) для контроля невязки по формуле fβ = [β]n – [β]T. Âû-

числяют поправки в углы, уравненные углы и дирекционные у˝глы

сторон.

511

После этого вычисляют приращения координат для всех сторон ходов. Порядок уравнивания приращений аналогичен рас˝- смотренному для углов и не требует особых пояснений. Применяемые при этом формулы и правила приведены ранее. Вычислен˝ие координат узловой точки приведено в таблице 18.2.

Уравнивают координаты в той же последовательности, что и углов, используя в основном формулы, приведенные при урав˝нивании приращений координат в системе теодолитных ходов с˝ одной узловой точкой.

Системы тахеометрических ходов в плановом отношении уравнивают так же, как системы теодолитных ходов, а в высот˝- ном — как системы нивелирных ходов. Отличие может быть только в определении весов координат и высот узловых точек (ил˝и приращений и превышений по ходам). Так, если длины сторон ходов определялись по нитяному дальномеру, то веса коорди˝нат вычисляют по формуле

pi = k/[S2]i,

ãäå [S2]i — сумма квадратов длин сторон хода.

По этой же формуле находят и веса высот.

18.3. СПОСОБ ПОСЛЕДОВАТЕЛЬНЫХ ПРИБЛИЖЕНИЙ

Этот способ чаще всего применяют в тех случаях, когда сист˝ема ходов имеет большое число узловых точек или когда число п˝оли-

гонов (вместе с дополнительными) больше числа узловых точ˝ек. Неизвестные величины, непосредственно связанные с узловыми

точками или узловыми линиями

(высоты, координаты узловых то-

чек или дирекционные углы узло-

вых линий), получают последовательными приближениями.

Рассмотрим этот способ на примере нивелирной сети.

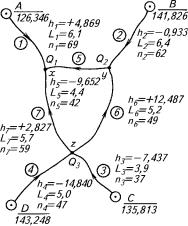
Уравнивание системы нивелир-

ных ходов. Пусть требуется уравнять систему нивелирных ходов (рис. 18.3) с исходными высотами

Рис. 18.3. Схема уравнивания нивелирной сети способом последовательных приближений

512

ÍÀ, ÍÂ, ÍÑ, ÍD, измеренными превышениями по ходам hi, ñ äëè-

нами ходов Li и числом станций ïi (i = 1, 2, …, 7). Надо найти высоты õ, ó è z узловых точек Q1, Q2, Q3.

Согласно параметрическому способу метода наименьших квадратов можно составить систему уравнений с неизвестн˝ыми

высотами x, y, z и привести их к виду

ãäå = (èëè ði = k/Li) — вес измеренного превышения hi (i = 1, 2, …, 7).

Нетрудно видеть, что эти равенства имеют вид формулы сред˝-

него весового. Поэтому их легко написать без вывода. Написанные равенства являются исходными для получения

приближений неизвестных, кроме нулевых.

В качестве нулевых приближений, являющихся начальными,

могут быть приняты произвольно выбранные числа. Но для то˝го

чтобы процесс решения был более коротким, их получают пут˝ем передачи высот на узловые точки от ближайших исходных пун˝к- тов или по ходам от исходных пунктов с меньшим числом стан˝-

ций, например:

Так как равенства (18.6) используют для определения последовательных приближений несколько раз, то для сокращения вы˝- числительной работы их приводят к виду

513

Величины ¢ ¢¢ ¢¢¢ называют приведенными весами. Их сумма для каждой узловой точки равна единице. Это свойство пр˝и-

веденных весов используют для контроля правильности их в˝ы-

числений.

Первое приближение õ¢ получают из первого равенства (18.7), подставив в него вместо ó è z их нулевые приближения

В результате подстановки во второе равенство вместо õ è ó èõ

Первое приближение z¢ находят, подставив в третьей равенство вместо õ è ó их первые приближения õ¢ è ó¢, ò. å.

На основании равенства (18.7) так же находят вторые прибли-

жения õ², ó², z², затем третьи — õ²¢, ó²¢, z²¢ и т. д., используя каж-

дый раз при подстановке в правые части равенств вместо не˝известных их самые последние приближения.

Таким образом, k-е приближения определяют по формулам:

Процесс приближений заканчивают, когда два следующих дру˝г за другом приближения для всех неизвестных будут одинако˝выми. Эти приближения и будут окончательными (уравненными) зна˝че- ниями неизвестных x, y, z.

Полученные значения высот узловых точек принимают за ис-

ходные, и сеть распадается на ряд изолированных ходов, каж˝дый из которых уравнивают отдельно по правилу, принятому для ˝оди-

ночного хода.

Пример уравнивания нивелирной сети (см. рис. 18.3) приведен в таблице 18.4.

514

18.4. Уравнивание нивелирной сети способом приближений

ÍÀ = 126,346 ì; ÍÂ = 141,826 ì; ÍÑ = 135,813 ì; ÍD = 143,248 ì.

515

В графе 1 таблицы 18.4 записывают номера определяемых (узловых) пунктов, во второй — номера исходных пунктов, с кот˝орыми непосредственно связан каждый определяемый пункт. В гр˝афе 3 — превышения по ходам-звеньям от исходных пунктов к опр˝еделяемым, а в графах 4, 5, 6 — соответственно число станций в ход˝е

(или его длину), веса превышений и приведенные веса. Для кон˝т- роля правильности выписки превышений подсчитывают их су˝мму в графе 3. Она должна быть равна сумме превышений по ходам, начинающимся от пунктов исходной сети.

Затем приступают к вычислению приближений высот узловых˝ точек. Начинают с вычисления нулевых приближений по форму˝- лам (18.6), т. е. для каждой точки нулевое приближение высоты получают путем передачи с исходного пункта по ходу с мень˝шим числом станций (или меньшей длины).

Полученные нулевые приближения записывают в соответств˝у- ющих строках и подчеркивают. При записи последующих прибл˝и- жений повторяющиеся целые их части опускают.

Первые, а затем и последующие приближения получают как средние весовые значения из высот, получаемых по всем схо˝дящимся к определяемой точке ходам, беря за исходные самые п˝о- следние приближения высот соседних пунктов и используя п˝ри этом приведенные веса. Получаемые приближения — средни˝е весовые значения — записывают в соответствующей графе в нижней части блока, соответствующего определяемому пункту. Вычи˝сление приближений заканчивают, когда два следующих один за ˝другим приближения высот будут одинаковыми для всех определ˝яемых пунктов. Последние приближения являются искомыми выс˝о- тами.

Далее контролируют вычисления и оценивают точность изме˝- рений. Для этого вычисляют поправки υi, получаемые вычитанием

результатов, записанных в графе 14 приближений, из соответс˝тву-

ющих окончательных значений высот. Находят произведения˝piυi

и их сумму [pυ] для каждого пункта. Теоретически эта сумма дол-

жна быть равна нулю [pυ] = 0, но вследствие погрешностей округ-

лений может несколько отличаться от нуля. Считают, что выч˝ис-

ления проведены верно, если [pυ] < [p]. Оценивают точность результатов нивелирования по формулам:

ãäå N — число ходов-звеньев; t — число узловых точек; òêì — средняя квадрати- ческая погрешность нивелирования хода длиной 1 км; Li — длина i-õîäà.

В сумму [pυ2] поправки υi должны входить один раз (см. табл. 18.4).

516

Следует иметь в виду, что при малом числе N—t полученное

значение òêì малонадежно.

Контрольные вопросы и задания

1. Каковы назначение и способы построения съемочных сетей˝? 2. Какие слу- чаи уравнивания съемочных сетей по способу среднего весо˝вого (узловых точек) вы знаете? 3. Как уравнивают нивелирные ходы с одной узловой˝ точкой (вычисление среднего весового значения высоты узловой точки, вычи˝сление невязок по ходам, оценка точности высоты узловой точки)? 4. Как уравнив˝ают теодолитные ходы с одной узловой точкой, углы (вычисление среднего вес˝ового значения дирекционного угла, вычисление невязок по ходам, оценка точ˝ности измерения угла), приращения координат (вычисление среднего весовог˝о значения координат узловой точки, вычисление невязок в приращениях координа˝т, вычисление приращений координат, оценка точности положения узловой точ˝ки)? 5. Как уравнивают нивелирные ходы способом последовательных приближ˝ений (получение высот узловых точек в первом, втором и последующих приближе˝ниях, получение окончательных высот и оценка точности результатов уравн˝ивания)?

517

à ë à â à 19

ГЛОБАЛЬНАЯ СПУТНИКОВАЯ НАВИГАЦИОННАЯ СИСТЕМА ПОЗИЦИОНИРОВАНИЯ

∙

19.1. ОБЩИЕ СВЕДЕНИЯ. ИСТОРИЧЕСКАЯ СПРАВКА. ПРИНЦИП РАБОТЫ СИСТЕМЫ И ЕЕ ДОСТОИНСТВА

В конце ХХ века в геодезии нашли распространение принципиально новые методы и средства измерений, базирующиеся н˝а

использовании искусственных спутников Земли (ИСЗ), получ˝ивших название спутниковое позиционирование.

Спутниковое позиционирование — определение местополо˝же-

ния (координат пункта или движущегося объекта) при помощи˝

спутниковых навигационно-геодезических систем (СНГС). Эт˝о направление получило широкое применение в различных обл˝а-

стях человеческой деятельности.

Координаты пунктов (объектов) нужны не только геодезис-

там, но и морякам, авиаторам, военным, участникам различных˝ экспедиций и многим другим потребителям. Если раньше для

создания геодезической основы приходилось строить доро˝госто-

ящие сети различных конфигураций, закрепляемые на местности специальными центрами с наружными знаками (пирамидами, сигналами) для обеспечения взаимной видимости между пунк˝та-

ми, то появление спутниковых систем сделало эти работы не˝- нужными. С помощью только одного спутникового приемника возможно определить координаты объекта с метровой точно˝- стью, что достаточно не только для навигационных, но и в ряд˝е случаев для земельно-кадастровых, геологических, мелиора˝тивных и других работ. Применяя два приемника, можно получить сантиметровую и даже миллиметровую точность взаимного п˝о-

ложения пунктов, что обеспечивает решение практически вс˝ех

геодезических задач.

Спутниковое позиционирование базируется на электронных˝

методах геодезических измерений, в первую очередь на элек˝тронной дальнометрии, которые широко применяют в наземной гео˝- дезии. В случае спутниковых измерений эти методы претерпе˝ли существенные изменения, обусловленные спецификой прохо˝ждения сигналов на космических трассах.

К первому поколению спутниковых систем позиционировани˝я до 70-х годов можно отнести Транзит (США) и Цикада (СССР). В 1984—1993 гг. в России с помощью системы Транзит создана доплеровская геодезическая сеть (ДГС).

518

Все эти системы обеспечивали точность получения координ˝ат

50…100 м и отличались малой оперативностью: для достижения высокой точности требовались несколько прохождений ИСЗ˝ в «поле зрения» приемника, при этом перерывы между прохожде˝- ниями спутников, например в системе «Транзит», составляли˝ пол-

тора часа. Это послужило основанием для разработки систем˝ второго поколения — глобальных спутниковых систем.

Применяя глобальные системы, получают координаты в любой˝ точке Земли в любой момент времени с сантиметровой точнос˝тью.

Это стало возможным благодаря увеличению высот орбит спу˝тни-

ков до 20 тыс. км и числа самих спутников до 24. Приемники спутниковых сигналов созданы с применением высоких техн˝ологий, поэтому они малы по размерам и сравнительно недороги˝. Все

это позволяет рассматривать глобальные системы как ново˝е до-

стояние цивилизации.

Âмире существуют две глобальные системы: американская —˝

GPS и российская — ГЛОНАСС.

GPS (Global Positioning System — Глобальную Систему Пози-

ционирования) первоначально называли NAVSTAR (1973). Система находится в ведении Министерства обороны США. Запуск

спутников первого блока осуществлен в 1978 г. Эксплуатирует˝ся с 1995 г. До недавнего времени система была открыта для гражда˝н-

ского пользования только в режиме пониженной точности; дл˝я режима высокой точности требовался санкционированный д˝ос-

туп. В 2000 г. это ограничение снято, и сейчас GPS открыта для

всех и в режиме высокой точности.

ГЛОНАСС — Глобальная навигационная спутниковая система. Ее разработки начаты в 1970 г. В 1982 г. выведены на орбиты пер-

вые ее спутники серии КОСМОС. В 1993 г. система официально

принята в эксплуатацию Министерством обороны РФ. В 1996 г.

ГЛОНАСС развернута полностью. В ней навигационный режим повышенной точности оставлен для санкционированных пол˝ьзователей (военных), а режим пониженной («стандартной») точн˝о- сти доступен гражданским пользователям. Уже работают при˝емные устройства, одновременно использующие и GPS и ГЛОНАСС.

Â1989 г. начали создание Европейской системы координат EUREF, которая базируется на методе GPS и опирается на основ-

ные спутниковые станции, задающие всемирную систему коор˝ди-

нат ITRF. На территории 15 стран было заложено 92 пункта с та-

ким расчетом, чтобы в каждой стране было не менее трех пунк˝тов

сгущения. Расстояния между пунктами составили 300…500 км. По

результатам уравнивания точность системы оценена на уро˝вне 3…4 см.

Â1999 г. Европейский парламент поддержал решение Европейского космического агентства ESA о создании нового поколен˝ия спутниковой системы GALILEO, которая будет включать 30 спут-

ников (из них 3 резервных), расположенных на высоте 23 200 км и

519

вращающихся в трех орбитальных плоскостях, наклоненных н˝а

56° к плоскости экватора. Таким образом, с учетом спутников ˝GPS и ГЛОНАСС в распоряжении пользователей будет 80 космическ˝их аппаратов (КА), покрывающих весь земной шар.

Принцип работы глобальной системы состоит в том, что прием-

ники GPS-сигналов на Земле используют спутники в качестве исходных (опорных) пунктов для определения своего местоп˝о-

ложения. Это известная в геодезии пространственная обратная линейная засечка, когда на пересечении трех сферических п˝о-

верхностей (рис. 19.1) определяют координаты искомого пунк-

та. Измеряя время прохождения сигнала от спутника до прие˝м- ника, можно определить расстояние до спутника. По трем измеренным дальностям Di (i = 1, 2, 3) координаты определяемой

точки x, y, z получают из решения трех уравнений (уравнений

сферы) вида

ãäå xi, yi, zi — известные координаты точек, от которых измеряли расст˝ояние (центры сфер).

При применении изложенного геометрического принципа оп˝- ределения местоположения к глобальным спутниковым сист˝емам

возникают две особенности. Одна из них состоит в том, что ис˝ход-

ными пунктами (пунктами с известными координатами) являю˝тся движущиеся спутники, а определяемыми (неподвижными или дви-

жущимися) — пункты (спутниковые приемники), находящиеся˝ на Земле. Другая особенность работы системы состоит в том, чт˝о

вследствие несинхронности хода часов на спутнике и в прие˝мнике

520