48

где uA , uB , uC , u f - напряжения на фазных обмотках якоря и обмотке воз-

буждения;

iA , iB , iC , if , i1d , i1q - токи в фазных обмотках якоря, обмотке возбужде-

ния, продольном и поперечном демпферных контурах;

R , Rf , R1d , R1q - активные сопротивления фазных обмоток якоря, обмот-

ки возбуждения, продольного и поперечного демпферного контуров. Дифференциальное уравнение моментов, действующих на ротор машины,

можно записать как

где M мех - момент механических сил;

M эл - момент электромагнитных сил;

J - момент инерции агрегата;

ω - угловая частота вращения ротора.

Поскольку многие индуктивности и взаимные индуктивности, входящие в выражения для потокосцеплений (4.1), зависят от угла γ и, соответственно, от

времени, то дифференциальные уравнения (4.4) являются уравнениями с переменными коэффициентами, что значительно усложняет задачу анализа переходных процессов в синхронной машине. Вследствие этого часто применяют линейные преобразования фазных переменных к некоторым новым переменным, позволяющим получить уравнения с постоянными коэффициентами.

4.4. Линейные преобразования уравнений

Линейные преобразования уравнений состоят в замене в этих уравнениях исходных переменных новыми переменными, линейно связанными с исходными. При этом коэффициенты линейного преобразования могут быть и функциями времени.

Линейному преобразованию можно дать геометрическую интерпретацию. Синусоидальные токи трехфазной системы можно представить тремя вектора-

ми IA , IB и IC , вращающимися относительно полюса с частотой сети. Проек-

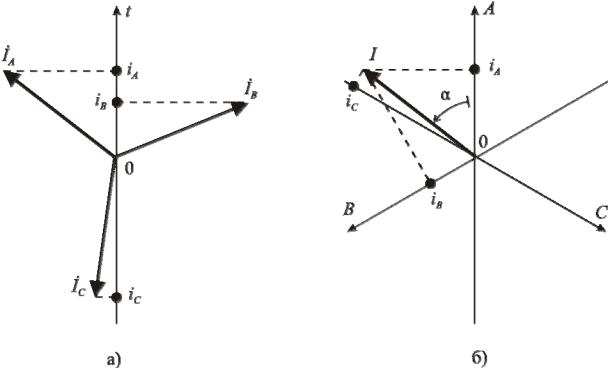
ции этих векторов на ось времени t определяют мгновенные значения фазных токов iA , iB , iC (рис. 4.2а). Однако эти же мгновенные значения токов можно

получить, проектируя единый вектор I на три оси времени, каждая из которых совпадает с магнитной осью соответствующей фазы (рис. 4.2б). Такой вектор называется изображающим (или обобщенным) вектором трехфазной систе-

мы. При его вращении в ту же строну, что и системы трех векторов, чередование осей времени фаз нужно изменить на противоположное.

49

Рис. 4.2. Определение мгновенных значений фазных токов: а - как проекций векторов токов на ось времени; б - как проекций изображающего вектора тока на магнитные оси фаз машины

С помощью изображающего вектора можно определять не только токи, но и любые другие фазные величины fA , fB , fC , например намагничивающие

силы, потокосцепления, напряжения, изменяющиеся в общем случае по произвольному закону, но при условии, что всегда

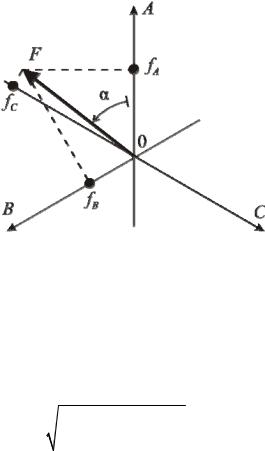
Это условие следует из принятого способа нахождения мгновенных значений фазных величин fA , fB , fC как проекций некоторого вектора F на три

оси, сдвинутые на 120 эл. град. (рис. 4.3), т. е.

а сумма этих проекций при любом законе изменения вектора F во времени равна нулю.

50

Рис. 4.3. Определение мгновенных значений фазных величин с помощью изображающего вектора.

Следовательно, каким бы образом не изменялись во времени фазные величины fA , fB , fC , удовлетворяющие условию (4.6), в каждый момент времени

их значения можно рассматривать как проекции некоторого вектора F на магнитные оси машины. Вектор F однозначно определен по модулю и положению относительно магнитных осей машины. Его модуль

Если фазные величины изменяются по синусоидальному закону и симметричны, то изображающий вектор вращается с постоянной скоростью, а его конец движется по окружности. Если же эти величины несимметричны, хотя и изменяются по синусоидальному закону и удовлетворяют условию (4.6), то изображающий вектор вращается с переменной скоростью, а его конец движется по эллипсу. В общем случае изображающий вектор вращается с переменной скоростью, а его конец описывает сложную кривую.

В любой момент времени изображающий вектор тока якоря направлен из центра расточки статора в направлении той точки зазора, в которой в данный момент результирующая намагничивающая сила максимальна. Из этого следует, что он может рассматриваться как ток якоря некоторой воображаемой машины, отличающейся от реальной тем, что вместо трех фазных обмоток на якоре она имеет только одну одноосную, но вращающуюся обмотку, магнитная ось которой в любой момент времени совпадает по направлению с изображающим вектором тока, причем действие этого тока эквивалентно суммарному действию токов трех фаз якоря реальной машины.

Возможность представления трехфазной системы векторов изображающим вектором существенно упрощает выражение связи между статором и ро-

51

тором, что в свою очередь позволяет в дифференциальных уравнениях переходного процесса освободиться от переменных коэффициентов.

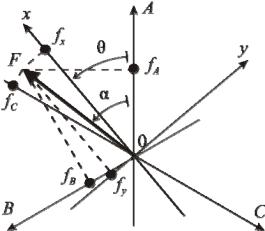
Изображающий вектор позволяет выполнить разные линейные преобразования, так как последние по существу сводятся к изменению системы координат. На рис. 4.3 изображающий вектор F определен в трехосной системе координат (фазные оси времени). Тот же вектор можно выразить также в произвольной двухосной системе координат. В качестве такой системы координат удобнее всего выбрать декартовые ортогональные координаты, например x, y, как показано на рис. 4.4. Такое преобразование координат с точки зрения математических операций соответствует замене переменных.

Рис. 4.4. Изображающий вектор и его проекции на магнитные оси фаз и оси x, y

где θ - угол сдвига оси x относительно магнитной оси фазы А.

Переход из системы координат x, y в систему фазных координат и наобо-

и

52

Выражения (4.12) получены в предположении, что всегда выполняется условие (4.6). Тем не менее, они справедливы и тогда, когда это условие не выполняется. Только в последнем случае при линейных преобразованиях необходимо помимо переменных fx и fy необходимо вводить третью переменную ве-

Таким образом, три переменные в фазных координатах можно однозначно заменить тремя переменными в координатах x, y, 0.

Переход от трехосной к двухосной системе координат по существу сводится к тому, что трехфазная машина заменяется эквивалентной двухфазной. Угол θ определяет пространственное положение магнитных осей обеих обмоток такой машины.

При анализе переходных процессов в электрических машинах используют различные системы координат, выбор которых позволяет или упростить дифференциальные уравнения, описывающие переходный процесс, или даже исключить из них периодические коэффициенты. С этой целью оси располагают неподвижно или относительно якоря, или относительно ротора, в зависимости от того, где имеется электрическая или магнитная несимметрия. Применяется также и система координат, оси которой вращаются в пространстве с синхронной скоростью.

Переходные процессы в асинхронных машинах, а также несимметричные режимы синхронных машин удобно исследовать в системе координат, неподвижной в пространстве. Такую систему координат называют системой α, β.

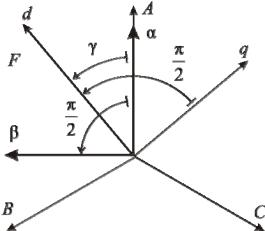
При этом ось α совмещают с магнитной осью фазы А электрической машины

(рис. 4.5).

53

Рис. 4.5. Системы координат α, β и d, q.

Исключить из дифференциальных уравнений, описывающих переходный процесс, переменные коэффициенты можно путем введения системы координат жестко связанной с ротором. При этом оси системы координат совмещают с продольной и поперечной осями ротора. Эту систему координат обозначают d, q (рис. 4.5). Здесь угол γ = ωt + γ0 является функцией времени и отражает вра-

щение ротора с угловой частотой ω, которая в общем случае может быть переменной. Если условие (4.6) не соблюдено, к координатам d, q должна быть добавлена третья координата 0, которая определяет нулевую составляющую переменных величин.

Переход к системе координат d, q, 0 физически означает замену реальной трехфазной обмотки якоря синхронной машины двухфазной, причем оси двух обмоток взаимно перпендикулярны, совпадают с осями d и q ротора, т. е. вращаются вместе с ротором с той же частотой вращения. Такая машина в магнитном отношении оказывается симметричной при любом положении ротора, вследствие чего индуктивности всех ее обмоток постоянны, а взаимные индуктивности между обмотками постоянны или равны нулю. Поэтому дифференциальные уравнения напряжений имеют постоянные коэффициенты, что существенно облегчает их решение.

Связь между переменными в системах координат А, В, С и d, q, 0 можно получить из (4.12)-(4.14), приняв θ = γ,