№4. Определить наибольшую площадь равнобедренного треугольника, боковая сторона которого равна l.

№5. Вычислить предел функции по правилу Лопиталя

№6. Исследовать функцию и построить её график

№7. Вычислить объём тела, образованного вращением вокруг оси Ох фигуры, ограниченной линиями

№8. Найти область сходимости степенного ряда

№9. В урне 6 белых и 4 черных шара. Из этой урны извлечены на удачу 5 шаров.

Какова вероятность того, что 2 из них белые, а 3 черные?

№10. 4 стрелка независимо друг от друга стреляют по одной мишени, делал каждый по одному выстрелу. Вероятности попадания для данных стрелков равны 0,4;0,6;0,7;0,8;после стрельбы в мишени обнаружены 3 пробоины. Найти вероятность того, что промахнулся четвертый стрелок.

Вариант №5.

№1.Найти базисное решение для системы уравнений (одна из свободных переменных - x₁) .

№2. Составить уравнение линии, для каждой точки которой отношение расстояний до точки А(-1;0) и до прямой х=-4 равноПолученное уравнение привести к каноническому виду и построить кривую.

№3. Найти собственные значения и собственные векторы линейного преобразования, заданного в некотором базисе матрицей

.

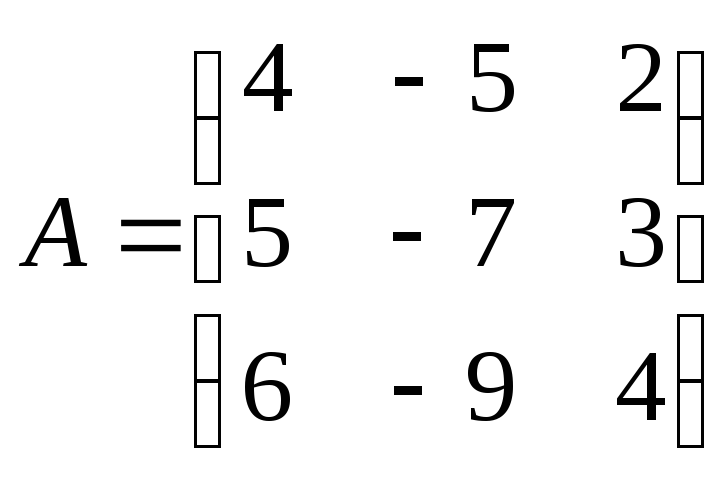№4. Сечение тоннеля имеет форму прямоугольника, завершенного полукругом. Периметр сечения равен 18м. При каком радиусе полукруга площадь сечения будет наибольшей?

№5. Вычислить предел функции по правилу Лопиталя

№6. Исследовать функцию и построить её график

№7. Вычислить объём тела, образованного вращением вокруг оси Ох фигуры, ограниченной линиями

№8. Найти область сходимости степенного ряда

№9. В урне 10 шаров, из которых 2 белых,3 черных и 5 синих. Наудачу извлечены 3 шара. Какова вероятность того, что все 3 шара разного цвета.

№10. Из 18 стрелков 5 попадают в мишень с вероятностью 0,7; 8-с вероятностью 0,6 и 5-с вероятностью 0,5. Наудачу выбранный стрелок не попал в мишень. К какой группе вероятнее всего принадлежит это стрелок?

Вариант №6.

№1. Найти базисное решение для системы уравнений (одна из свободных переменных - x₅) .

№2. Составить уравнение линии, для каждой точки которой её расстояний до точки А(2;1) равно расстоянию до прямой у=-1. Полученное уравнение привести к каноническому виду и построить кривую.

№3. Найти собственные значения и собственные векторы линейного преобразования, заданного в некотором базисе матрицей .

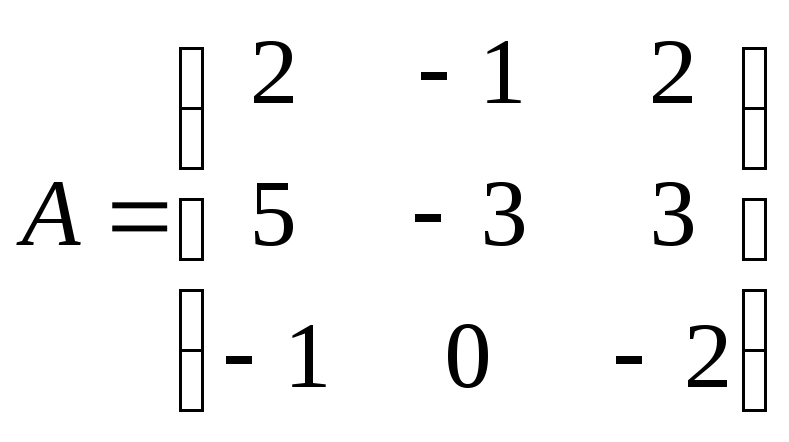№4. Нужно огородить проволокой земельный участок, прилегающий к стене. Проволоки имеется 200 м. Ограда делается в форме прямоугольника, Какова должна быть длина и ширина участка, чтобы площадь получилась наибольшей?

№5. Вычислить предел функции по правилу Лопиталя

№6. Исследовать функцию и построить её график

№7. Вычислить объём тела, образованного вращением вокруг оси Оу фигуры, ограниченной линиями

№8. Найти область сходимости степенного ряда

№9. В урне 4 белых и 5 черных шара. Из этой урны извлечены 2 шара.

Какова вероятность того, что они одного цвета?

№10. Бросается монета, и если она падает так, что сверху оказывается герб, вынимаем один шар из урны I; в противном случае из урны –II. Урна I содержит 3 красных и 1 белый шар. Урна II содержит 2 красных и 3 белых шара. Какова вероятность того, что шар вынимался из I урны, если он оказался красным?

Вариант №7.

№1. Найти базисное решение для системы уравнений (одна из свободных переменных - x₁)

№2. Составить уравнение линии, для каждой точки которой её расстояний до точки А(2;-1) равно расстоянию до прямой у=2. Полученное уравнение привести к каноническому виду и построить кривую.

№3. Найти собственные значения и собственные векторы линейного преобразования, заданного в некотором базисе матрицей .

№4. На оси параболы y² = 2px дана точка на расстоянии a от вершины. Найти абсциссу ближайшей к ней точки кривой.

№5. Вычислить предел функции по правилу Лопиталя

№6. Исследовать функцию и построить её график

№7. Вычислить объём тела, образованного вращением вокруг оси Оу фигуры, ограниченной линиями

№8. Найти область сходимости степенного ряда

№9. В группе 25 студентов, из них 5 отличников. Наугад отобрано 7 студентов. Какова вероятность того, что среди отобранных окажутся 3 отличника.

№10. Три самолета производят бомбометание по некоторой цели. Каждый самолет сбрасывает по одной бомбе. Вероятности попадания бомб в цель соответственно равны 0,3;0,4;0,35. Какова вероятность того, что в цель попали 2 бомбы?

Вариант №8.

№1. Найти базисное решение для системы уравнений (одна из свободных переменных - x₄) .

№2. Составить уравнение линии, для каждой точки которой её расстояний до точки А(4;-1) равно расстоянию до прямой у=1. Полученное уравнение привести к каноническому виду и построить кривую.

№3. Найти собственные значения и собственные векторы линейного преобразования, заданного в некотором базисе матрицей .