4.2.3 Discrete Filter (Дискретний Фільтр) і Discrete-Time Fcn (Дискретна Передавальна Функція)

Обидва блоки являють собою дискретну динамічну ланку загального виду з передавальною функцією поліноміального типу з тією лише різницею, що поліноми блоку Discrete-Time Fcn мають незалежною змінною оператор z (див. формулу (4.9)), а поліноми блоку Discrete Filter – z ^-1 (див. формулу (4.10)):

Способи введення векторів коефіцієнтів степеневих поліномів чисельника (Numerator) і знаменника (Denominator) і їхня інтерпретація аналогічні таким для блоку Transfer Fcn (див. п. 3.2.3).

Блок Discrete-Time Fcn базується на різновидності математичного опису дискретних ланок, що використовується у поширенні Control System Toolbox, а блок Discrete Filter – на опису, що використовується у поширенні Signal Processing Toolbox.

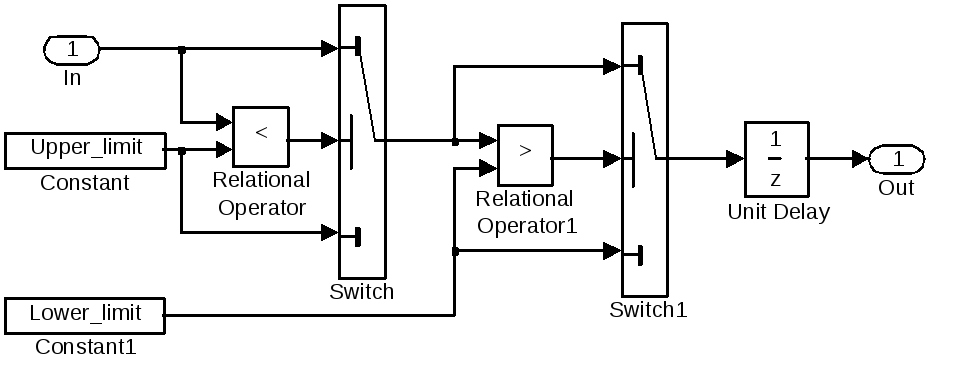
Рис. 4. 4. Модель блоку запізнення на період дискретності з обмеженням вихідного сигналу

4.2.4 Discrete Zero-Pole (Дискретні Нулі-Полюси)

Являє собою дискретну динамічну ланку загального виду з ПФ (4.11), де

K – коефіцієнт підсилення (Gain);

– нулі (Zeros);

– полюси (Poles).

Вектори нулів і полюсів можуть уводитися тими ж трьома способами, що і вектори степеневих поліномів блоку Transfer Fcn.

4.2.5 Discrete State-Spase (Дискретний Простір Станів)

Забезпечує моделювання дискретної динамічної ланки загального вигляду за її описом у просторі станів (див. рівняння (4.1)-(4.6)).

Вхідними параметрами блоку є матриці A, B, C, D, вектор початкових умов (Initial conditions) і період переривання (Sample time).

4.2.6 Zero-Order Hold (Екстраполятор Нульового Порядку)

Вимірює вхідний сигнал у дискретні моменти часу (2.1) і утримує значення цього сигналу на виході протягом періоду дискретності.

. (4.19)

4.2.7 First-Order Hold (Екстраполятор Першого Порядку)

В пакеті MATLAB 4.x блок First-Order Hold (FOH) мав структурну схему, зображену на рис. 4.5, а. Він вимірював вхідний сигнал у дискретні моменти часу (2.1) і формував вихідний сигнал у вигляді ламаної лінії, яка складалась з відрізків прямих, що з'єднують між собою 2 сусідні обмірювані точки входу з запізнюванням на період дискретності.

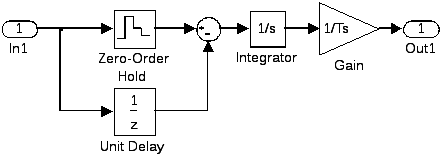
а)

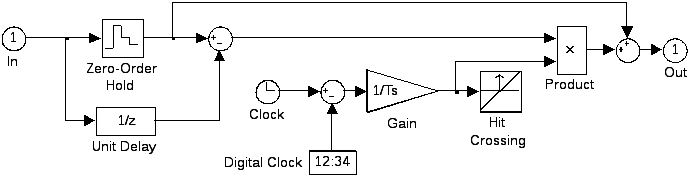
б)

Рис. 4.5. Моделі екстраполяторів першого порядку в пакеті MATLAB:

а) версій до 4.x; б) версій, починаючи з 5.х

Починаючи з MATLAB 5.x, структуру блоку FOH було змінено у відповідності з рис. 4.5, б, що, на наш погляд, виявилось не дуже вдалим рішенням. Про це свідчать подані на рис. 2.6 графіки перетворення вхідної синусоїди екстраполяторами нульового і першого порядків з наведеними на рис. 4.5 структурними схемами.

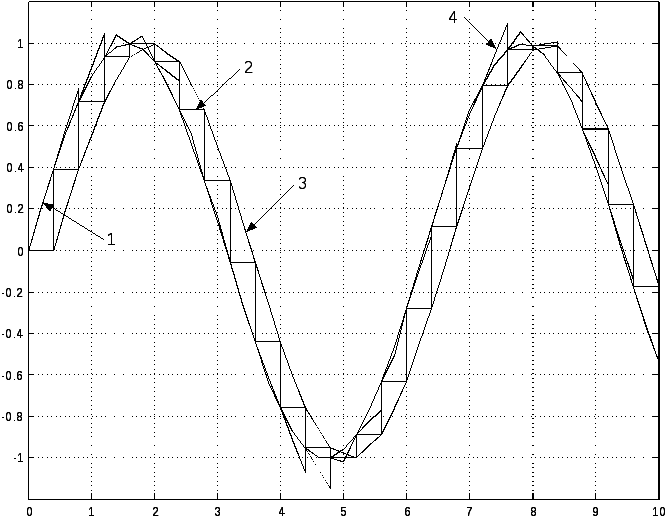
Рис. 4.6. Вхідний синусоїдальний сигнал (1) та результати перетворення

його екстраполяторами нульового порядку (2) та екстраполяторами

першого порядку, побудованими за схемами рис. 4.5, а (3) та рис. 4.5, б (4)

4.3 Індивідуальні завдання

1) Дослідити роботу блоку Discrete-Time Integrator з різними методами чисельного інтегрування при відпрацьовуванні ступінчатого, лінійного, та синусоїдального сигналів. Пояснити характер перехідних процесів.

2) Розробити дискретний інтегратор, здійснюючий чисельне інтегрування методом Сімпсона за рівнянням

. (4.20)

Приєднати його до моделі, отриманої при виконанні попереднього пункту завдання.

3) Створити екстраполятор першого порядку за схемою рис. 4.5, а та порівняти його роботу з роботою бібліотечних блоків First-Order Hold та Zero-Order Hold.

4) Зібрати модель, що складається із двох послідовно з‘єднаних дискретних блоків з різними періодами дискретності за даними табл. 4.1.

5) Порівняти перехідні функції цифро-аналогових моделей, що складаються з послідовно з‘єднаних дискретного інтегратора та неперервної аперіодичної ланки, замкнених одиничним зворотним зв‘язком.

(В одной схеме интегратор с ограничением, а в другой – последовательное соединение интегратора и ограничения)

6) Розробити дискретний інтегратор, здійснюючий чисельне інтегрування методом Сімпсона, з обмеженням вихідного сигналу. Приєднати його до моделі, отриманої при виконанні попереднього пункту завдання. Довести адекватність розробленого блоку