Лабораторная работа №1 Исследование линейных электрических цепей постоянного тока.

Цель работы: экспериментально проверить: выполнение законов Ома и Киргофа для цепей постоянного тока; методы расчета разветвленных цепей постоянного тока - метод наложения и метод двух узлов.

В неразветвленных цепях постоянного тока (рис.1.1) ток в цепи и падения напряжения на участках цепи определяются по закону Ома:

Разветвленная цепь с одним источником э.д.с. (рис.1.2) путем последовательных преобразований приводится к схеме рис. 1.1.

При определении токов, разветвляющихся в две параллельные ветви, удобно использовать формулу "разброса":

В разветвленных цепях с несколькими э.д.с. (рис.1.3) по любому замкнутому контуру должен выполнятся второй закон Киргофа:

для внешнего контура:

I₁R₁- I₂R₂ = E₁-E₂ ;

для внутренних контуров:

I₁R₁+ I₃R₃ = E₁ ;

I₂R₂+ I₃R₃ = E₂ .

Метод наложения . Сущность метода наложения основывается на принципе суперпозиции, заключающегося в том, что ток в отдельной ветви линейной разветвленной цепи равен алгебраической сумме токов в данной ветви, обусловленных действием каждой из э.д.с. в отдельности, причем остальные источники напряжения закорачиваются, а источники тока размыкаются. Таким образом, метод наложения позволяет заменить расчет сложной разветвленной цепи с несколькими э.д.с. соответствующим количеством расчетов цепей с одной э.д.с.

Метод двух узлов. Очень часто встречаются электрические цепи, состоящие из нескольких параллельно соединенных ветвей, т.е содержащие два узла. Разность потенциалов между двумя узлами U₃₀ определяется по формуле:

где E_i, I_i берутся со знаком " + ", если они направлены от узла 0 к узлу 1, и со знаком " - ", если наоборот.

Ток в каждой ветви определяется по закону Ома для участка цепи:

Порядок выполнения работы.

1. Собрать схему рис. 1.1. Измерить ток в цепи, э.д.с. источника и падения напряжения на резисторах R₁ и R₃.

2. Собрать схему рис.1.2. Измерить токи в ветвях схемы и падения напряжения на участках цепи.

3. По схеме рис.1.4 проверить метод наложения. Для этого исключить вначале из схемы источник Е₂ и измерить токи в ветвях схемы ( можно использовать результаты, полученные в п. 2).Затем из схемы рис.1.4 исключить источник Е₁ (схема рис.1.3) и вновь измерить токи в ветвях схемы. Для проверки метода наложения измерить токи в ветвях схемы рис.1.4, т.е. при действии обеих э.д.с.

4. В схеме рис.1.4 измерить напряжение между двумя узлами схемы, а также падения напряжения на резисторах R₁ и R₂.

Содержание отчета.

Для каждого эксперимента в отчете предоставляются: схема, измеренные значения токов и напряжений, проверка измеренных величин по формулам.

По результатам п.1 проверяется выполнение закона Ома для участка цепи и для полной цепи; по результатам п.2- выполнение законов Киргофа.

По результатам п.3 проверяется справедливость метода наложения путем сравнения алгебраической суммы токов в каждой ветви при действии каждой э.д.с. в отдельности с соответствующими токами для схемы с двумя э.д.с. Для проверки результатов, полученных в п.3, схема рис. 1.4 рассчитывается по методу наложения.

Необходимо также определить токи в ветвях схемы рис.1.4, используя значение напряжения между двумя узлами, измеренное в п.4.

Кроме того, значения токов в ветвях схемы рис.1.4 необходимо определить, используя метод контурных токов.

Лабораторная работа №2

Исследование линейных электрических цепей переменного тока.

Цель работы: экспериментально проверить выполнение законов Ома и Киргофа для цепей переменного тока, определить фазовые соотношения между напряжениями и токами в схеме.

В цепях переменного синусоидального тока кроме активных сопротивлений (резисторов) используются реактивные элементы: конденсаторы и индуктивности. В соответствии с законом Ома в дифференциальной форме для активного сопротивления R, индуктивности L и конденсатора С можно получить выражение для тока и напряжения на каждом виде элементов в цепях переменного тока

( i = I_msint):

для активного сопротивления R:

для индуктивности L:

для конденсатора С:

или если U_C = U_m sint, то

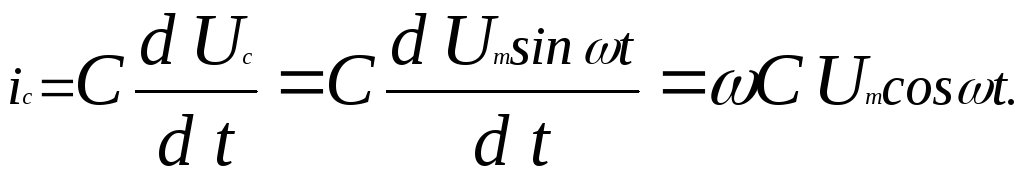
Отсюда следует, что в активном сопротивлении ток и напряжение совпадают по фазе, в индуктивности напряжение опережает ток на , в конденсаторе напряжение отстает от тока на.

При последовательном соединении R,L и С, когда через элементы цепи протекает один и тот же ток, падение напряжения на элементах цепи будут ориентированы относительно тока в соответствии с указанным выше, и поэтому второй закон Киргофа для цепей переменного тока рассматривается в векторной форме. При параллельном соединении R,L и C общей величиной для всех элементов является напряжение, а токи в ветвях будут ориентироваться относительно напряжения, поэтому первый закон Киргофа также выполняется в векторной форме.

В смешанных RC и RL цепях ток и напряжение сдвинуты друг относительно друга на угол меньше,

или .

Для удобства определения фазовых соотношений в электрических цепях переменного тока используют комплексный метод расчета цепей, в котором положение векторов напряжения и тока представляется на комплексной плоскости. Для реализации полученных фазовых соотношений между напряжением и током на элементах схемы сопротивления последних выражают в комплексной форме:

( Умножение величины на j равносильно повороту вектора на +, на -j — на -).

При использовании выражений для сопротивлений в комплексной форме для цепей переменного тока справедливы все методы расчета цепей постоянного тока. Отличие заключается лишь в том, что расчеты ведутся в комплексной форме, и каждый ток или напряжение на участке цепи выражается комплексным числом вида:

Обычно при расчетах цепей переменного тока одну величину (чаще всего напряжение источника питания цепи) направляют по действительной оси, т.е. начальная фаза этой величины принимается равной нулю, а все остальные полученные в ходе расчета величины будут иметь определенные фазы, т.е. характеризоваться определенным положением вектора на комплексной плоскости. Для каждой цепи переменного синусоидального тока можно построить векторную диаграмму, по которой можно судить о фазовых соотношениях между любыми соотношениями электрической цепи.

Порядок выполнения работы.

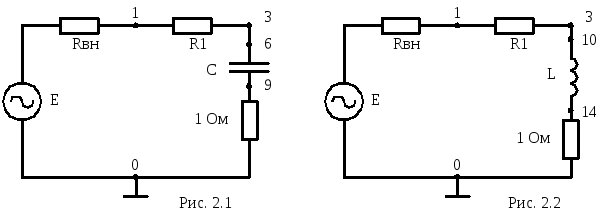
1. Собрать схему рис. 2.1. На вход схемы от генератора синусоидального напряжения подать напряжение U  5В. Измерить падения напряжения на участках цепи, действующее значение тока на частотах 200, 500, 1000, 2000 и 5000 Гц. Данные занести в таблицу:

f [Гц]	U10 [B]	U31 =UR[B]	U30 =UC[B]	U90=I [A]	Uрасч

2. С помощью осциллографа измерить фазовый сдвиг на частоте 1000 Гц.

3. Собрать схему рис.2.2. Повторить измерения, указанные в п.1. Данные занести в таблицу:

f [Гц]	U10 [B]	U31 =UR[B]	U30=UL[B]	U140=I [A]	Uрасч

4. С помощью осциллографа измерить фазовый сдвиг на частоте 1000 Гц.

Содержание отчета.

Для схем рис.2.1 и 2.2 проверить выполнение второго закона Киргофа для каждого эксперимента (колонка U_расч ).

Для частоты f = 1000 Гц построить векторные диаграммы и проверить полученные результаты комплексным методом.