§12. Найбільше й найменше значення функції в області

Відомо, що, якщо функція неперервна в обмеженій замкнутійобласті, то вона досягає свого найбільшого й найменшого значення. Якщо, крім того, функція має усередині області частинні похідні то ці значення вона досягає або усерединіобласті в стаціонарних точках, або на межі області.

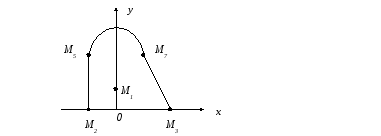
Приклад. Знайти найбільше й найменше значення функції вобласті ,обмеженої лініями:

Розв‘язування. 1) Знаходимо стаціонарні точки усередині області :

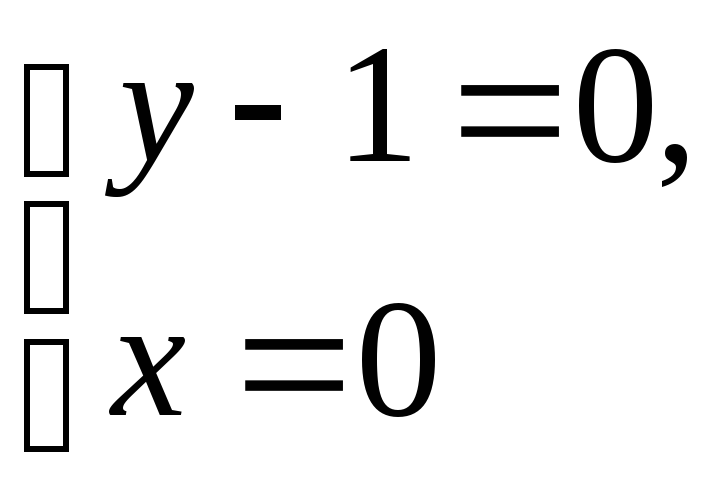–стаціонарна точка

2) Розглянемо функцію на межі області.

2.1) Це лінійна функція,свої найбільше й найменше значення досягає на кінцях проміжку: іМаємо щедві точки для дослідження: і.

2.2) Ця функція також лінійна, тому маємо щедві точки:і.

2.3) Ця функціяоднієї змінної досягає найбільшого й найменшого значення або усередині проміжку вточці, де , або на кінцях проміжку. Похіднаобертається в нуль у точках Отже, маємо щеточки: ,і.

3) Обчислюємо значення функції в знайдених “підозрілих” точках і виби-раємо з отриманого ряду чисел найбільше й найменше:

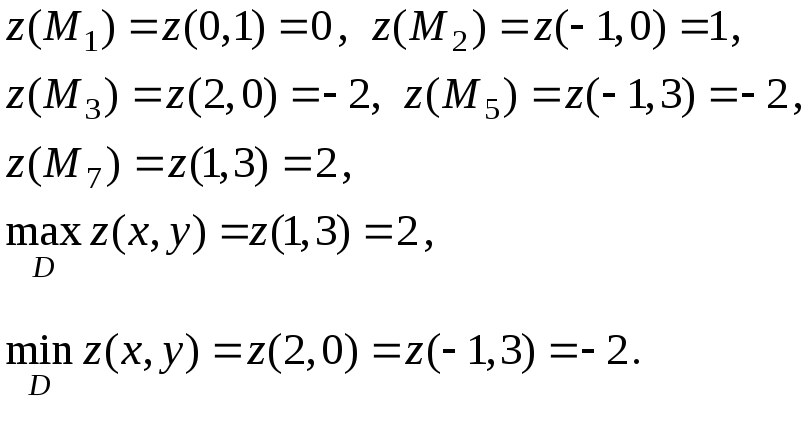
Лекція 21

§13. Похідна за напрямом. Градієнт

I Похідна за напрямом

В одномірному випадку похідна функції характеризує швидкість зміни функції в данійточці у напрямку осі . У двовимірному випадку частинні похідні функціїхарактеризують те ж саме унапрямку координатних осей.

Природно порушити питання про швидкість зміни функції уна-прямку довільної осі .

Нехай функція визначена в деякомуоколі точки й нехай вісьзаданакутами й, які вонаутворює із осями координат. Вісь зручно задавати її ортом: . Будемовважати, що вісь проходить через точку й нехайточка – довільнаточка, що лежить на осі. Тоді , тобто.

Означення 1. Нехай точка необмежено наближається доточки уздовж осі.Границя виду

(1)

називається похідною функції занапрямком осі вточці й позначається одним із символів

, ,.

Теорема 1. Нехай функція має в деякомуоколі точки неперервні частинні похідні першого порядку й нехай вісьутворює із осями координаткути й. Тоді похідна даної функції занапрямком осі вточці існує й виражається формулою

. (2)

Доведення. Нехай – поточнаточка осі . Тому що, ай усилу того, що , будемо мати:

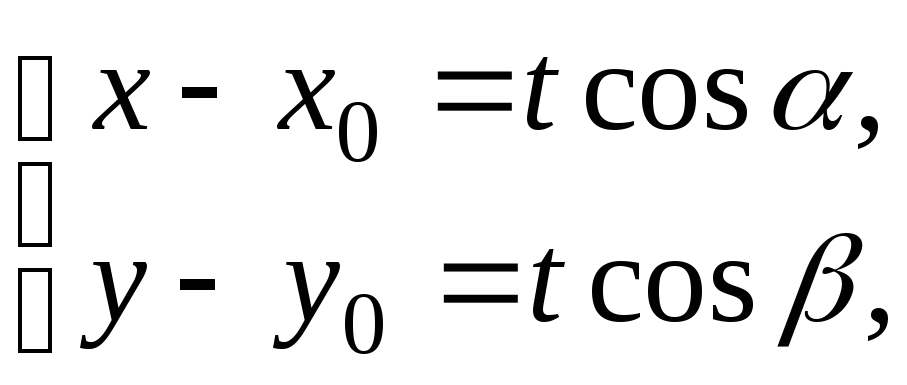
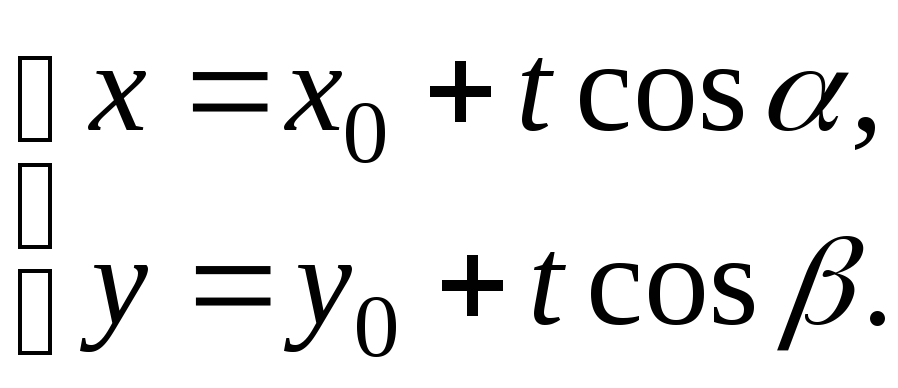
Тобто, координати поточної точки є функції параметра. Тоді:

,

і з (1) маємо:

. (3)

Остання границя є похідна функції в нулі. Похідна ж складної функціїіснує, тому щомає неперервні похідні, а її аргументий–диференційовані, при цьому:

.

Розглянемо останню рівність при йодержимо

.

Тепер формула (3) і доводить теорему.

Зауваження. У випадку функції трьох змінних і осі, що має ортформула (2)здобуває вид

.

Приклад. Обчислити похідну функції вточці занапрямком вектора , де.

Розв‘язування. Знайдемо одиничний вектор, що має даний напрямок:

, ,,

звідки ,. Далі, обчислимо частинні похідні даної функції вточці :,, звідки,. Тепер по формулі (2)одержимо

.

II Градієнт

Означення 2. Вектор, проекціями якого слугують частинні похідні функції , називається градієнтом функції

.

Для функції трьох змінних :

.

Зв'язок градієнта з похідною за напрямком дається наступною теоремою.

Теорема 2. Похідна функції за напрямком є проекція її градієнта на цей напрямок:

.

Доведення. Проекція вектора на вісь – це проекція вектора на орт осі. Проекцію же вектора на вектор можна знайти, використовуючи скалярний добуток:

.

З огляду на те, що й, причому,одержимо:

.

Права частина цієї рівності і є похідна за напрямком. Теорема доведена.

Наслідок 1. Похідна функції вточці занапрямком осі досягає максимуму, коли цейнапрямок збігається із градієнтом функції, причому

.

Таким чином, градієнт функції в даній точці характеризує напрямок і величину максимальної швидкості зростання функції в даній точці.

Наслідок 2. Похідна функції за напрямком, перпендикулярному її градієнту, дорівнює нулю.