§11. Екстремуми функції декількох змінних
Нехай
функція
визначена в деякій області
й нехай
– внутрішня точка
цієї області.
Означення 1. Говорять, що функція має в точці локальний максимум (мінімум), якщо існує такий окіл точки , у якому виконується нерівність
(
).
Якщо знак “=” досягається тільки в точці , то максимум (мінімум) називається власним, у противному випадку – невласним. Точки максимуму й мінімуму називаються точками екстремуму.
Теорема 1. (необхідна умова екстремуму). Якщо функція має екстремум у точці й має в цій точці частинні похідні першого порядку, то ці похідні обертаються в нуль у точці .
Доведення.
Нехай для визначеності
– точка
максимуму функції
.
Розглянемо
функцію однієї
змінної
Тоді в деякому околі
точки
,
тобто точка
– це точка
максимуму функції
.
Крім того,
– диференційована
в точці
,
тому що
.
З теореми Ферма випливає
,
й
.
Аналогічно доводиться й рівність
.
Означення
2.
Точки,
у яких всі частинні похідні першого
порядку
функції
обертаються
в
,
називаються стаціонарними точками
даної
функції.
Зауваження
1.
Якщо
– стаціонарна точка
функції
,
то дотична площина до поверхні, заданої
рівнянням:
,
у точці
має рівняння
,
тобто горизонтальна.
Зауваження
2.
Екстремуми
можуть бути не тільки в стаціонарних
точках,
але й у точках,
у яких хоча б одна з похідних
і
не
існує або має нескінченне
значення.
Зауваження
3.
Не у всякій стаціонарній точці
функція має екстремум.
Наприклад, для функції
точка
– стаціонарна: частинні похідні
=
y,
= x
дорівнюють
нулю на початку координат. Але в цій
точці
функція не має ні максимуму,
ні мінімуму, тому що
,
а в будь-якіому околі
цієї точки
функція
приймає як додатні
так і від‘ємні значення.
Щоб
сформулювати достатню
умову
екстремуму
функції двох
змінних
введемо
спеціальні позначення. Нехай
– стаціонарна точка
функції
й
нехай у її околі
існують неперервні частинні похідні
другого порядку. Позначимо
,
,
,
(нагадаємо,
що
)
і
.
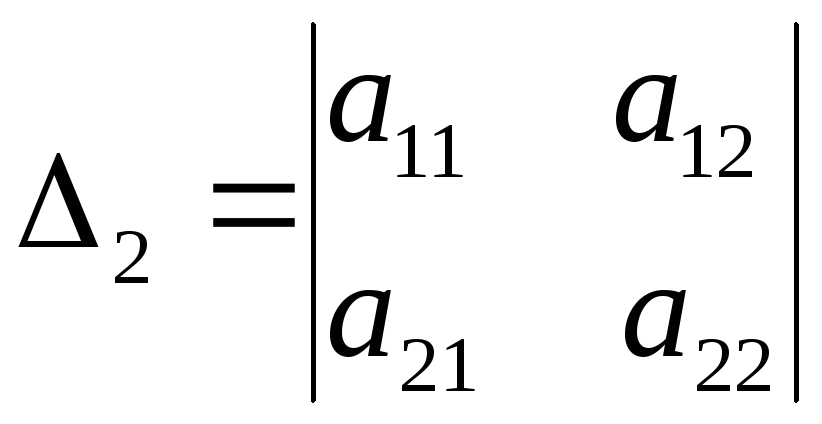Теорема 2 (достатня умова екстремуму).
1. Функція
z=
має у своїй стаціонарній точці
екстремум,
якщо
,
причому
– точка
мінімуму, якщо
,
і точка
максимуму, якщо
.
2. Якщо
,
то в точці
немає екстремуму.
3. Випадок
вимагає додаткового дослідження.
Розглянемо
тепер випадок функції
змінних
.
Нехай
точка
– стаціонарна точка,
тобто
Припустимо, що в деякому околі
цієї точки
існують неперервні частинні похідні
другого порядку. Позначимо
i,
j
= 1,2,…,n
.
Із цих
чисел складемо матрицю
.
Визначники, складені
з елементів
перших
рядків
і
стовпців,
називаються головними мінорами даної
матриці:
,
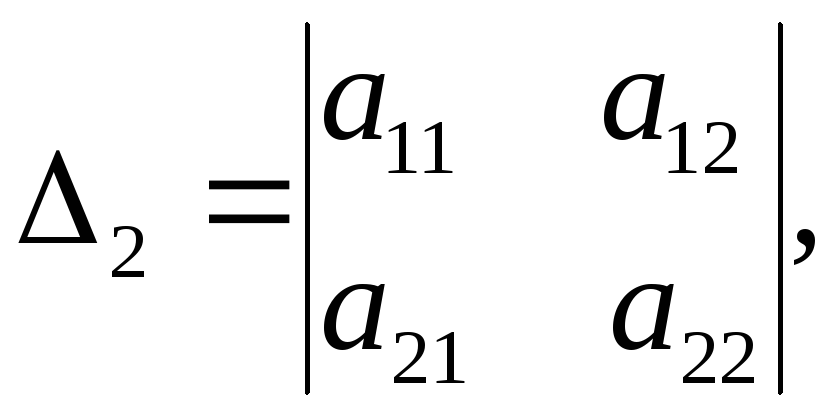
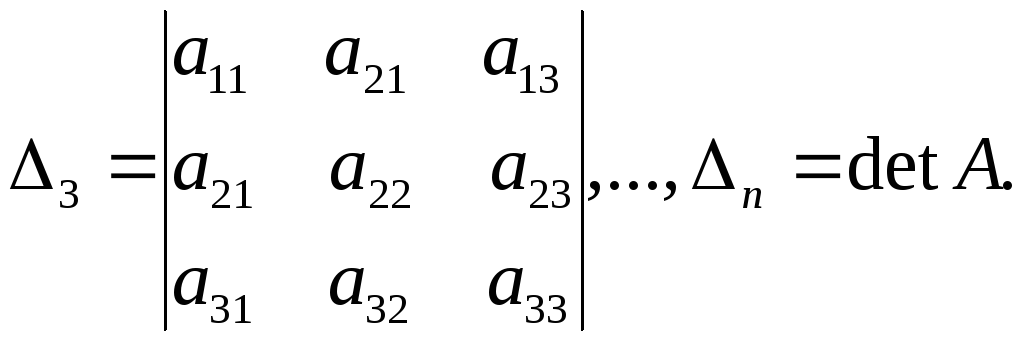
Теорема
3.
1) Якщо всі головні мінори позитивні,
то функція має в точці
локальний мінімум. 2) Якщо знаки мінорів
чергуються, причому
,
то
– точка
локального максимуму.
Приклад 1. Дослідити на екстремум функцію
.
Розв‘язування. Знаходимо частинні похідні першого порядку:
Знаходимо стаціонарні точки:
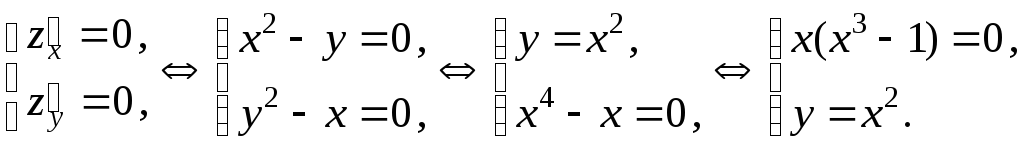
Маємо
дві
стаціонарні точки
й
.
Щоб дослідити
ці
точки,
обчислюємо похідні другого порядку:
Складемо із цих похідних визначник:
.
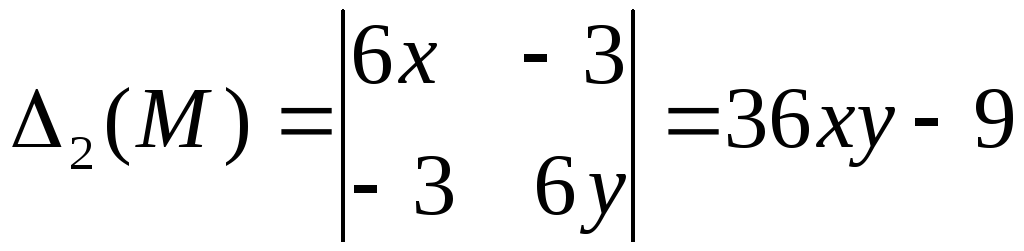У точці
:
отже, у точці
немає екстремуму.
У точці
:
отже, у точці
функція має екстремум;
тому що
то цей
екстремум
– мінімум.
Приклад 2. Дослідити на екстремум функцію трьох змінних
.
Розв‘язування.
і
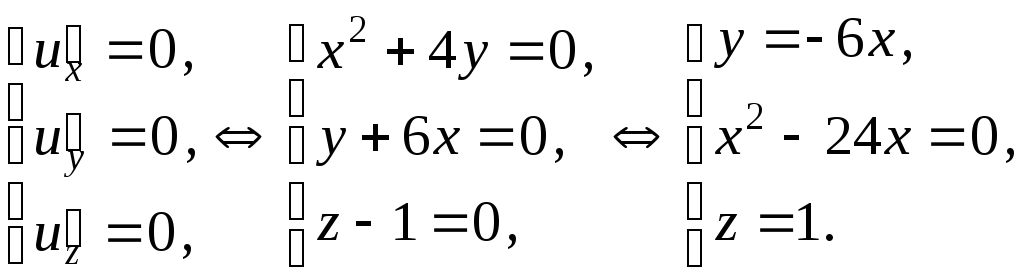
Маємо
дві
стаціонарні точки:
і
.
Далі:
,
,
,
,
.
Обчислимо ці похідні в точці й складемо матрицю
.
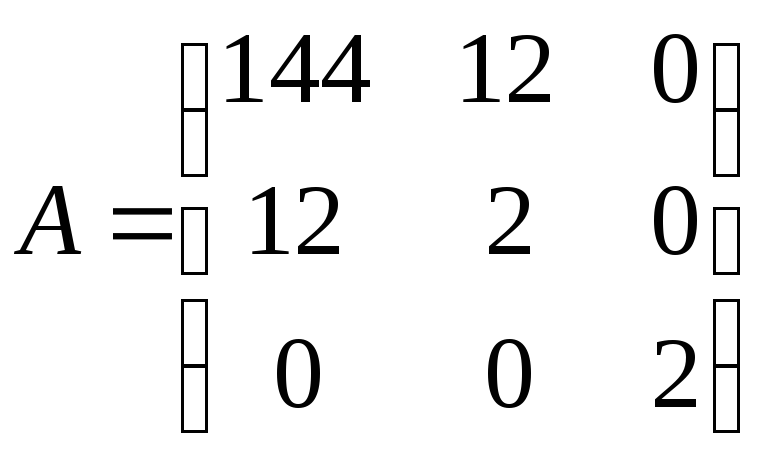Знайдемо головні мінори:
Всі
головні мінори позитивні,
значить
– точка
мінімуму.
У точці
матриця других
похідних
має вигляд
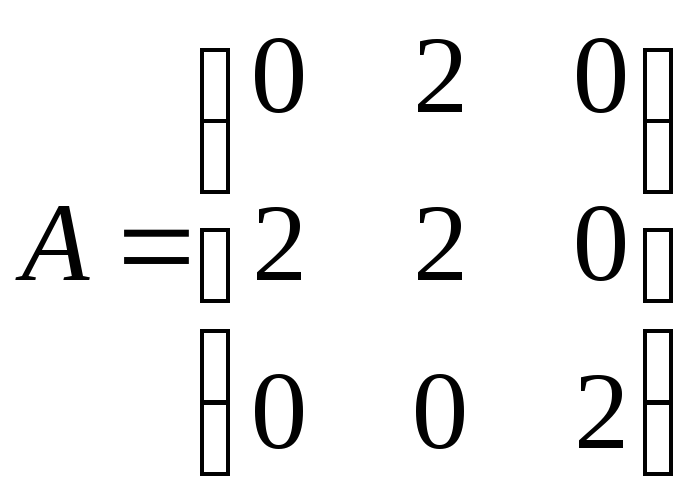
Мінор
Це означає, що потрібне додаткове
дослідження. У точці
функція дорівнює
В той же час, при зміні аргументів функції
уздовж прямої
функція має вигляд
і в як завгодно малому околі
точки
приймає як додатні,
так і від‘ємні значення. Отже,
у цій точці
немає екстремуму.