§2. Означення функції декількох змінних

Означення 1. Якщо кожній m-мірній точці М(х₁, х₂, … х^m) з деякої мно-жини D R^m поставлено у відповідність за деяким правилом одне певне число u, то говорять, що на D задана функція n змінних і пишуть: u = F(x₁, x₂,…x_n), або u = u(M).

Прикладом такої функції може слугувати середнє арифметичне коорди- нат точки:

.

Можна дати й інше, більш прозоре, означення функції, наприклад, двох змінних.

Означення 2. Нехай x, y, z – змінні величини. Якщо кожній парі можливих значень незалежних змінних х и у поставлено у відповідність за деяким правилом одне певне значення змінної z, то говорять, що z – є функція х и у і пишуть: z = f(x, y), або z = z(x, y), або z = z (M), де М(х, у).

Основний спосіб завдання функції – аналітичний у явній або неявній формі:

z = x² + y² , x² + y² + z² = R².

Якщо функція f(M) задана на множині D R^m, то цю множину називають областю визначення функції. Наприклад, для функції маємо:

,

а для функції –

Графік функції двох змінних z = z(x,y) – це поверхня в просторі R³ : .

§3. Границя функції декількох змінних. Неперервність

Для простоти надалі будемо розглядати функції двох змінних.

Означення 1. Число b називають границею функції z = z(x,y) у точці М₀(х₀,у₀) і пишуть

,

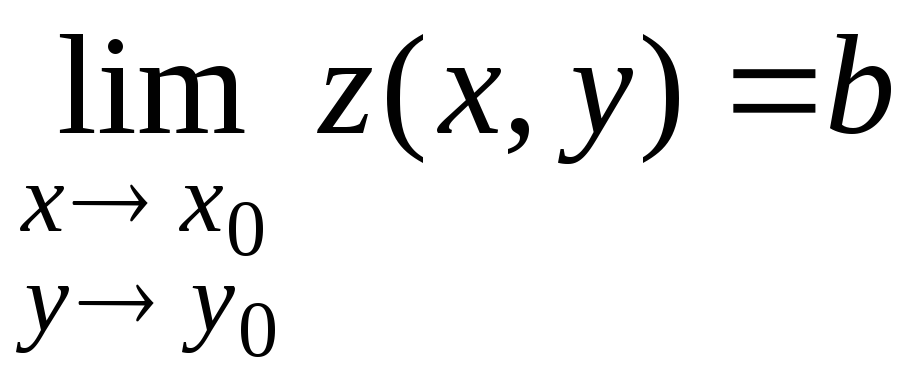якщо для будь-якої послідовності точок яка збігається до точки M₀ (тобто x_n→x₀, y_n→y₀), маємо

.

Всі властивості й теореми про границі функцій однієї змінної залишаються справедливі й для функцій декількох змінних (ФДЗ). Правда, для ФДЗ немає поняття однобічних границь.

Приклади.

1. Тому що sinα ~ α, при α → 0, то

2. Розглянемо функцію й послідовність точок

, що збігається до початку координат O(0,0). Відповідна послідовність значень функції

має границю, що залежить від послідовності {M_n}. Отже, границя функції на початку координат не існує.

Означення 2. Функція z(x,y) називається неперервною в точці , якщо

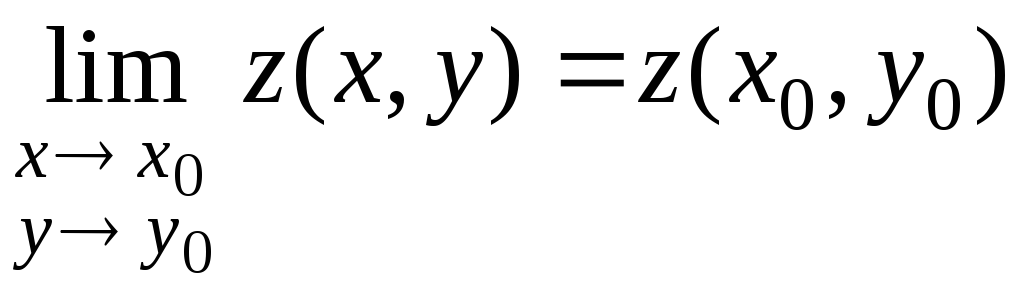. (1)

Означення 3. Функція z (x,y) називається неперервною в області G, якщо вона неперервна в кожній точці .

Властивості ФДЗ, неперервної в обмеженій замкнутій області, аналогічні властивостям функції однієї змінної, неперервної на замкнутому проміжку. Приведемо деякі з них.

1) Функція z(х,y), неперервна в обмеженій замкнутій області , обмежена в , і досягає найбільшого й найменшого значень.

2) Якщо z(х₀,y₀) , то в деякому околі точки функція зберігає знак.

Зауваження. Співвідношенню (1), що означає неперервність функції в точці, можна дати іншу форму.

Будемо називати повним приростом функції z(x,y) у точці

різницю:

Якщо позначити то неважко одержати твердження:

неперервність функції z(x,y) у точці рівносильна рівності

.

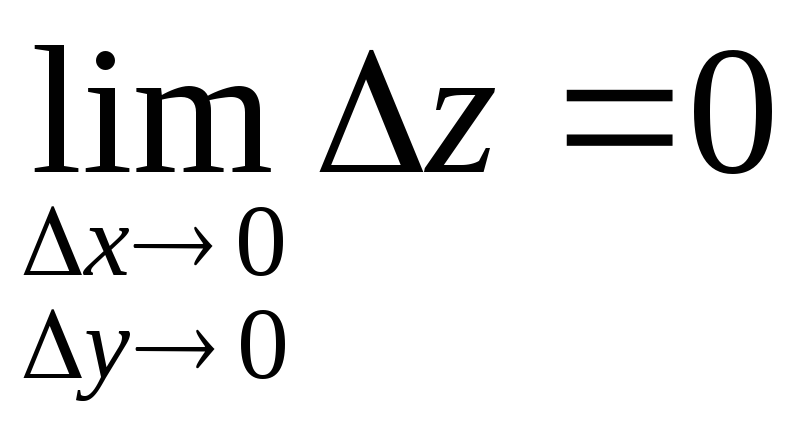Лекція 18

§4. Частинні похідні

Нехай функція z(x,y) визначена в деякому околі точки . Дамо змінної x приріст , тобто перейдемо від точки до точки . При цьому таке, що лежить у зазначеному околі точ-ки . Тоді відповідний приріст функції

називається частинним приростом функції z(x,y) у точці по змінній х.

Аналогічно визначається частинний приріст функції по змінній :

.

Означення. Границя виду називається частинною похідною функції z(x,y) у точці по змінній і позначається одним із символів:

.

Аналогічно визначається й частинна похідна по змінній :

.

З означення випливає, що частинна похідна функції двох змінних по змінній являє собою звичайну похідну функції однієї змінної f(x) = z(x,y₀). Тому частинні похідні обчислюються по формулах і правилам обчислення похідних функцій однієї змінної.

Приклади.

1.

2.

Зауваження. Графік функції z = z(x,y) є деяка поверхня у просторі. Тоді

–

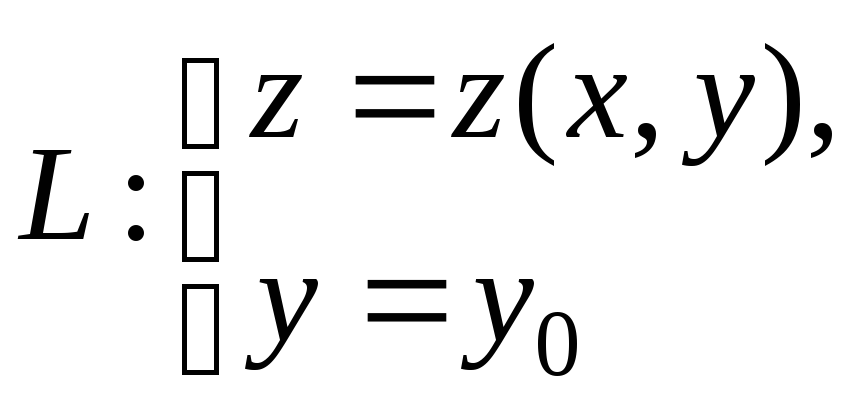це деяка крива (плоска) у просторі і є не що інше, як кутовий коефі-цієнт дотичної до L у точці ( ).