§12. Наибольшее и наименьшее значения функции в области
Известно, что,
если функция
непрерывна в ограниченной замкнутой
области, то она достигает своего
наибольшего и наименьшего значения.
Если, кроме того, функция имеет внутри
области частные производные
то эти значения она достигает либо
внутри облати в стационарных точках,
либо на гра-нице области.
Пример.
Найти наибольшее и наименьшее значение
функции
в области
,
ограниченной линиями:
Решение. 1) находим стационарные точки внутри области :
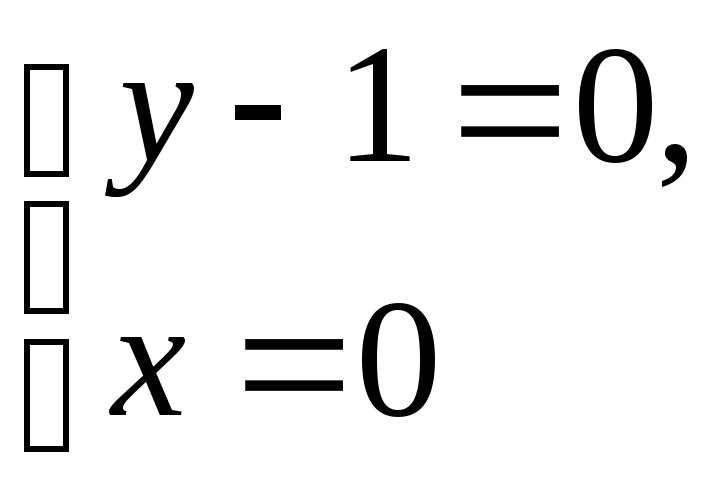– стационарная
точка
2) Рассмотрим функцию на границе области.
2.1)
Это линейная функция, свои наибольшее
и наименьшее значение достигает на
концах промежутка:
и
Имеем еще две точки подлежащие
исследованию:
и
.
2.2)
Эта функция также линейная, поэтому
имеем еще две точки:
и
.
2.3)
Эта функция одной пе-ременной достигает
наибольшего и наименьшего значения
либо внутри проме-жутка
в точке, где
,
либо на концах промежутка. Производная
обращается в ноль в точках
Итак, имеем еще точ-ки:
,
и
.
3) Вычисляем значения функции в найденных “подозрительных” точках и выбираем из полученного ряда чисел наибольшее и наименьшее:
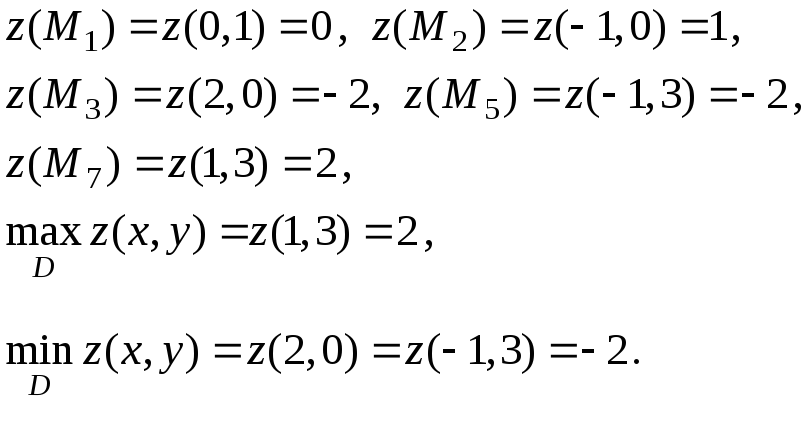
Лекция 21
§13. Производная по направлению. Градиент
I Производная по направлению
В одномерном случае
производная функции
характеризует скорость изменения
функции в данной точке в направлении
оси
.
В двумерном случае частные производные
функции
характеризуют то же самое в направлении
координатных осей.
Естественно
поставить вопрос о скорости изменения
функции
в направлении произвольной оси
.
Пусть функция
определена в некоторой окрестности
точки
и пусть ось
задана углами
и
,
которые она составляет с осями координат.
Ось удобно задавать её ортом:
.
Будем считать, что ось проходит через
точку
и пусть точка
– произвольная точка, лежащая на оси.
Тогда
,
т.е.
.
Определение 1. Пусть точка неограниченно приближается к точке вдоль оси . Предел вида
(1)
называется
производной функции
по направлению оси
в точке
и обозначается одним из символов
,
,
.
Теорема 1. Пусть функция имеет в некоторой окрестности точки непрерывные частные производные первого порядка и пусть ось образует с осями координат углы и . Тогда производная данной функции по направлению оси в точке существует и выражается формулой
.
(2)
Доказательство.
Пусть
– текущая точка оси
.
Так как
,
а
и в силу того, что
,
будем иметь:
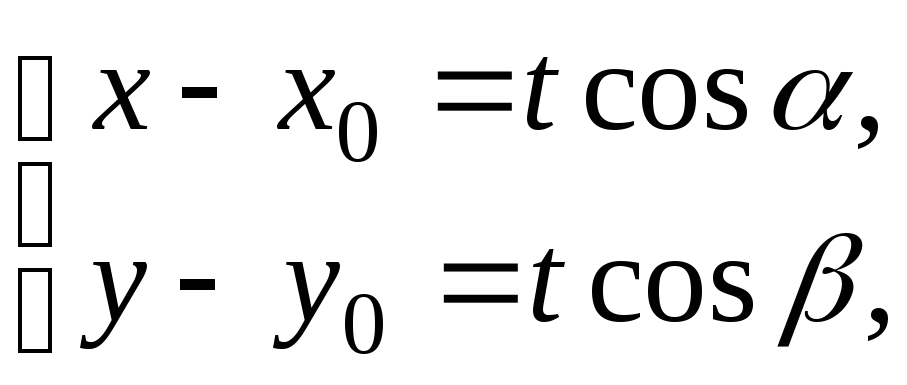
То есть, координаты
текущей точки
есть функции параметра
.
Тогда:
,
и из (1) имеем:
.
(3)
Последний предел
есть производная функции
в нуле. Производная же сложной функции
существует, ибо
имеет непрерывные производные, а её
аргументы
и
– дифферен-цируемы, при этом:
.
Рассмотрим последнее
равенство при
и получим
.
Теперь формула (3) и доказывает теорему.
Замечание.
В случае функции трёх переменных
и оси
,
имеющей орт
формула (2) приобретает вид
.
Пример.
Вычислить производную функции
в точке
по направлению вектора
,
где
.
Решение. Найдём единичный вектор, имеющий данное направление:
,
,
,
откуда
,
.
Далее, вычислим частные производные
данной функции в точке
:
,
,
откуда
,
.
Теперь по формуле (2) получим
.