§7. Сущестование и дифференцируемость неявной функции

Теорема. Пусть функция двух переменных и ее частные производ-ныеинепрерывны в некоторой окрестности точки, причем:аТогда уравнениеопределяет (в не-которой окрестности точки) единственную функцию. Эта функция дифференцируема и

(1)

Докажем формулу (1), принимая без доказательства существование и дифференцируемость неявной функции . То, что уравнениеопределяет некоторую функцию, означает следующее:(в не-которой окрестности точки). Продифференцируем это тождество почленно, используя формулу (2) предыдущего параграфа:

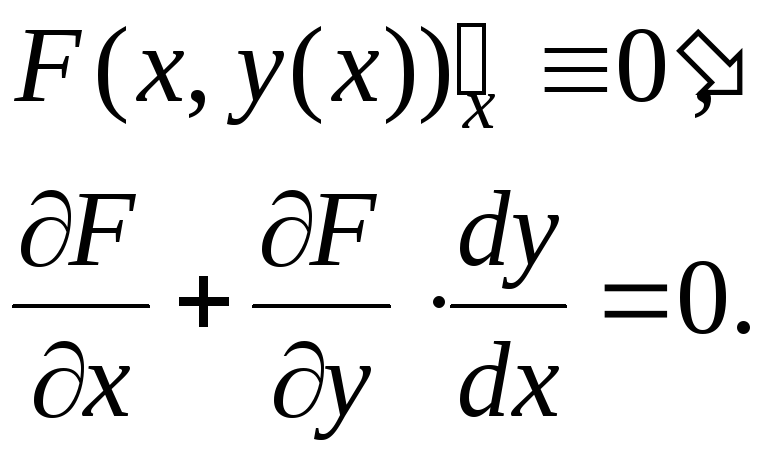
Из последнего равенства и вытекает формула (1).

Пример. Рассмотрим функцию и точкуВычислим производные:Нетрудно видеть, что все условия теоремы выполнены:непрерывны в окрестности точкии,Следовательно, в некоторой окрестности точки, уравнениеопределяет некоторую функцию, обращающую уравнение в тождество. Ее производная:

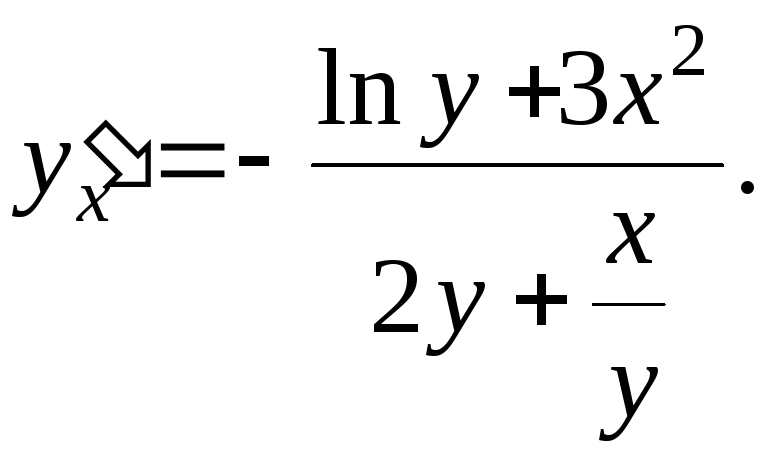
Замечательно, что по свойствам функции двух переменных , задан-ной непосредственно, мы можем судить о свойствах функции, для которой непосредственного задания мы не имеем.

Замечание 1. Геометрический смысл условия линия определяемая уравнениемимеет в точкеневертикальную касательную, т.е. саму линию можно понимать как график некоторой функции (в некоторой окрестности точкиМ₀).

Замечание 2. Теорема легко обобщается на случай неявных функций нескольких переменных.

Лекция 19

§8. Касательная к кривой в пространстве

I Вектор-функция и ее производная

Определение 1. Если каждому значению переменной t из некоторого мно-жества Т поставлен в соответствие некоторый вектор , то говорят, что на множествеТ задана вектор-функция

Определение 2. Вектор называют пределом вектор-функциив точкеи пишут , если.

Определение 3. Производной вектор-функции в точке называют предел

Если в пространстве задана декартова прямоугольная система координат, то вектор определяется своими проекциями, т.е.

или.

Таким образом, вектор-функция – это упорядоченная тройка обычных функций одной переменной. А так как

,

то определение 2 равносильно следующим трем равенствам

.

Аналогично для производной получаем

.

Будем откладывать векторы ,, от начала координат. Тогда их концы составят в пространстве некоторую линию, которую называют годографом вектор-функции . Например, для вектор-функциигодограф – это винтовая линия.

II Физический смысл производной вектор-функции

Положение точки М в пространстве можно задавать ее координатами (в не-которой системе координат), а можно задавать и радиус-вектором , гдеО – начало координат. Если точка М движется, то зависит от времени, т.е. движение точки в пространстве можно задавать вектор-функцией, гдеt – время из некоторого промежутка. Годограф этой функции – это траектория дви-жения. Производная – это вектор мгновенной скорости:

.

III Уравнения касательной

Линию в пространстве обычно задают системой параметрических урав-нений

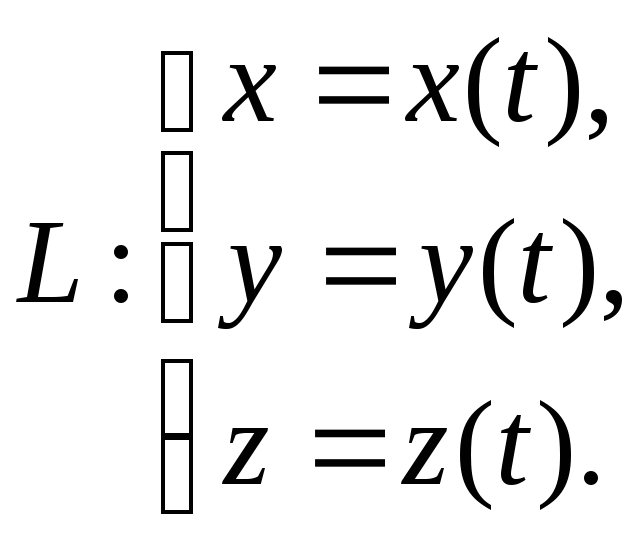
Однако, удобно такую линию понимать как годограф вектор-функции

.

Напомним, что, кратко говоря, касательная к линии L в ее точке –это пре-дельной положение секущей, когда точкастремиться квдольL. Другими словами, касательная в точке – это та прямая, проходящая через, направляющий вектор которой есть предел направляющего вектора секущей. ПустьиТогда

,

т.е. , а следовательно ислужат направляющими векторами секущей. Поэтому

Отсюда получаем два вывода:

1)вектор мгновенной скорости точки направлен по касательной к траек-тории движения;

2)канонические уравнения касательной к линии L в точке , которая соответствует значению параметра, имеют вид:

Пример. Показать, что касательные к линии образуют с осьюпостоянный угол.

Решение. Для винтовой линии направляющий вектор касательной . Если– угол между касательной и осью, то

.

Напомним, что – орт оси:. Значит,

.

Как видим, , а значит и, не зависят от параметра t, т.е =сonst.

Замечание. Нетрудно заметить, что для плоской линии

уравнение касательной имеет вид

Пример. Составить уравнение касательной к эллипсу

Решение. Пусть – точка касания, соответствующая значению параметра:. Тогда уравнение касательной:

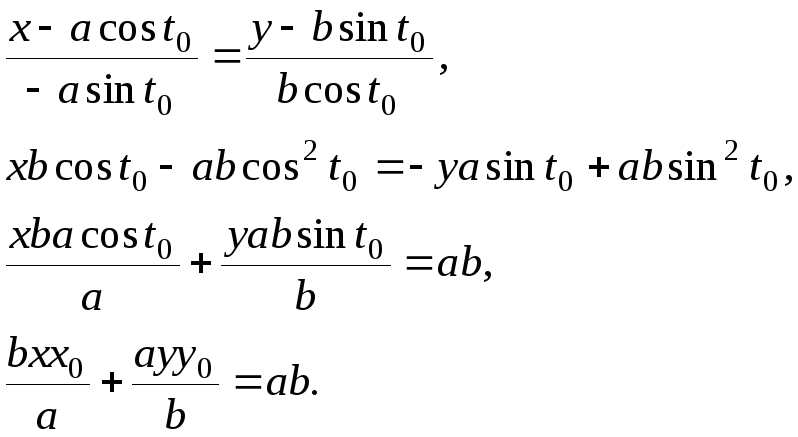
Разделив обе части последнего равенства на а ^.b, получим известную формулу для касательной к эллипсу в его точке :

.