§14. Метод наименьших квадратов

I Постановка задачи и суть метода

Предположим, что произведены измерения двух величин и, связанных некоторой зависимостью. Например,– температура растворителя,–количество растворяющегося вещества. Результаты измерений сведены в таблицу:

х			...
			…

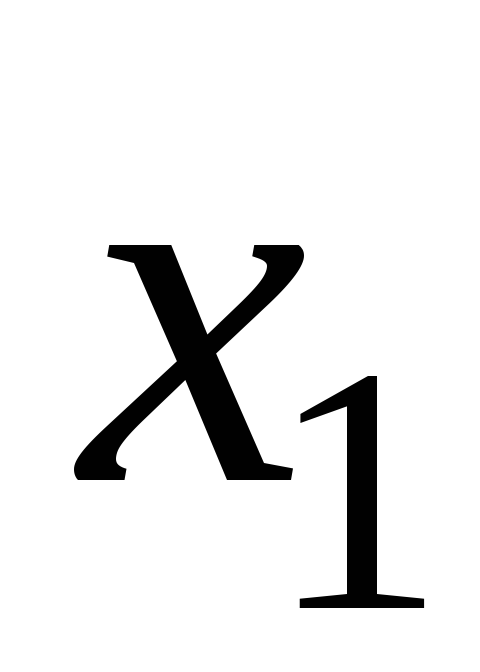
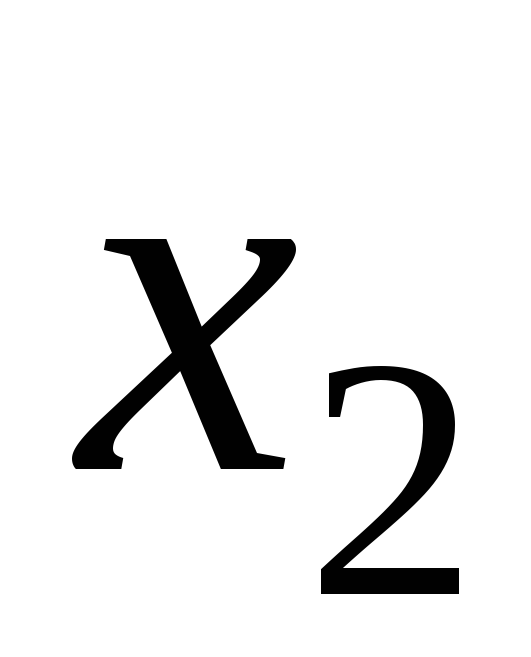
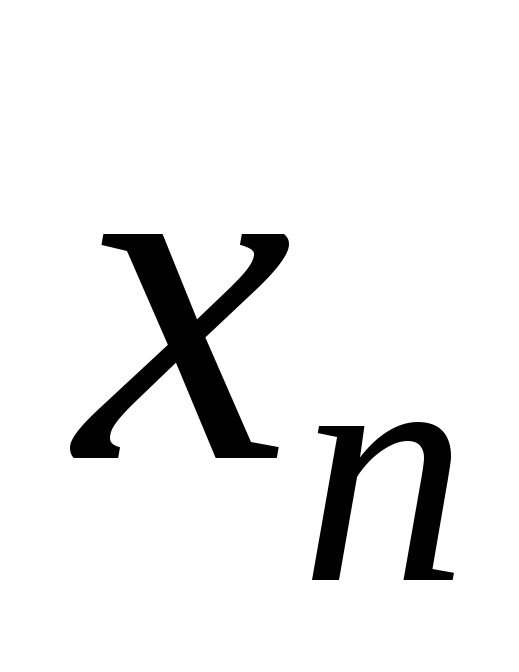
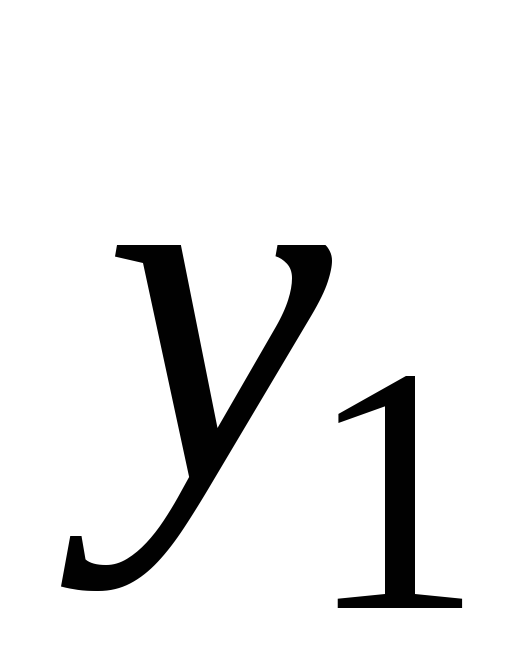
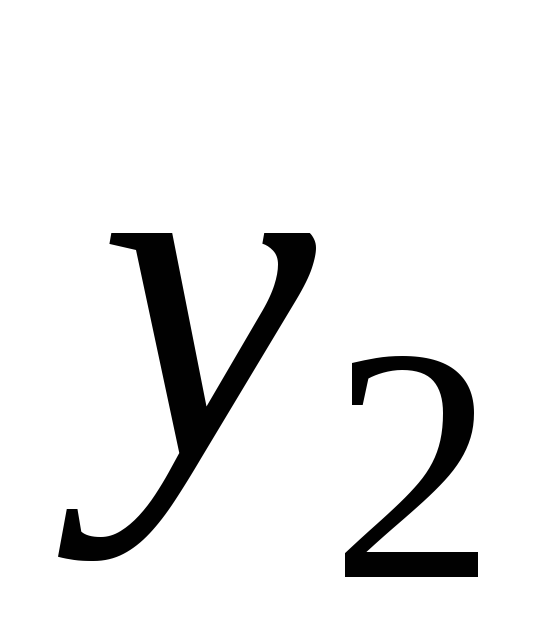
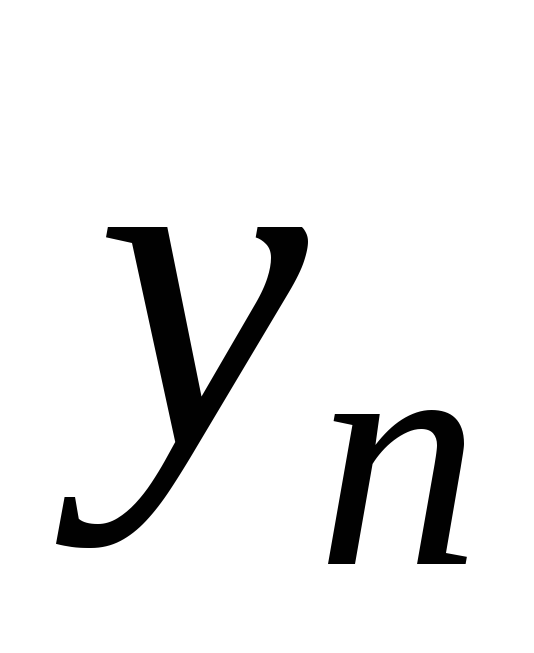
Измерения неизбежно содержат ошибки. Поэтому точки ,, не “лягут” точно на график функции. Например, для линейной зависимостикартинка может иметь вид:

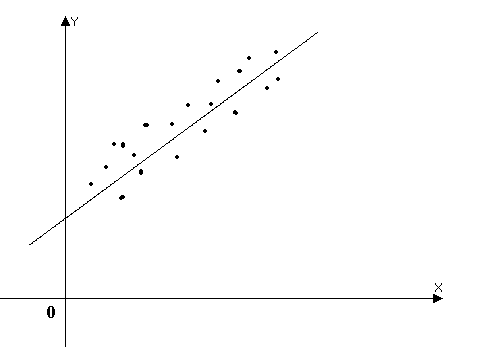
Задача состоит в таком выборе параметров функции , чтобы её график “наилучшим” образом вписывался во множество точек,. В качестве меры близости графика к этим точкам наиболее часто используется сумма квадратов отклонений наблюдённого значенияот теоретического значения:

Те значения параметров функции , которые доставляют этой сумме минимальное значение, считаются “наилучшими”.

В случае линейной зависимости “наилучшие” значенияиминимизируют сумму:

, (1)

т.е должны обращать в нуль частные производные и. Вычислим эти производные:

,

.

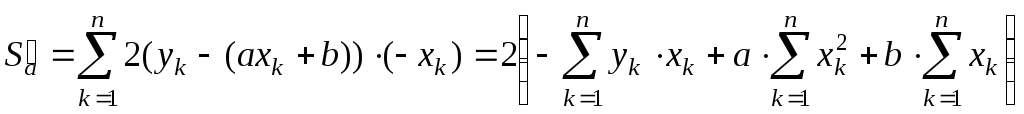Итак, для определения стационарной точки функции имеем т. н. систему нормальных уравнений:

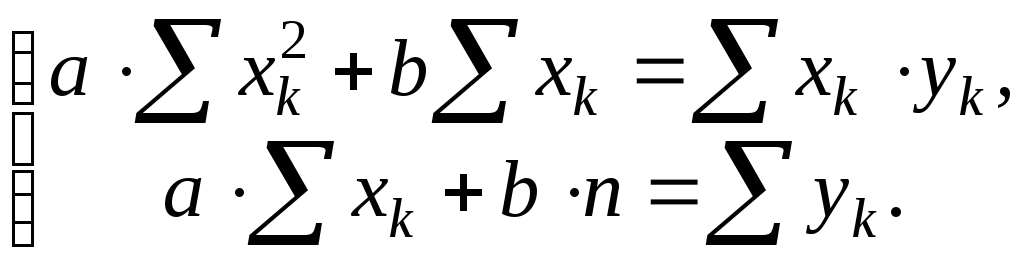(2)

II Одно полезное неравенство

Чтобы исследовать систему (2), а затем и стационарную точку, докажем одно неравенство.

Рассмотрим чисел, исключая случай. Обозначим– среднее арифметическое этих чисел:. Тогда:

Но сумма квадратов, стоящая в начале этой цепочки равенств, строго положительна (ибо не все одинаковые), следовательно, и

.

Из этого неравенства легко получить требуемое нам:

.

Замечание.Полученное неравенство есть частный случай неравенства Коши-Буняковского

,

которое является обобщением неравенства для векторов: .

III Исследование системы нормальных уравнений

Вернёмся к системе (2). Её определитель:

,

т.е. , следовательно система (2) имеет единственное решение, а функция (1) одну стационарную точку. Чтобы исследовать эту точку, найдём значения вторых производных функции (1) в этой точке:

, ,.

Определитель, составленный из этих чисел

,

значит в точке есть экстремум, а так как, то этот экстремум – минимум.

Итак, задача минимизации функции всегда имеет единственное решение.

Пример.Результаты измерений приведены в таблице:

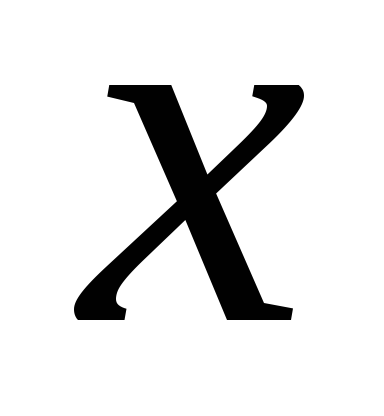
	–1	0	1	2	3	4	5
	3	2	2	1	2	1	0

Используя метод наименьших квадратов, определить “наилучшие” значения параметров линейной функции .

Решение.Вычислим коэффициенты системы нормальных уравнений (2):

, ,,.

Составим систему:

Её решение: ,. Линейная функция, которая “наилучшим” образом описывает результаты измерений, имеет вид:

.

130