
- •Раздел дифференциальное исчисление Тема введение в математический анализ
- •§1. Функции одной переменной: основные понятия
- •I Определение
- •II Способы задания функции
- •III Область определения и область значения функции
- •IV График функции
- •V Действия над функциями
- •VI Элементы поведения функции
- •VII Обратная функция
- •§2. Элементарные функции
- •I Основные элементарные функции
- •II Элементарные функции
- •III Примеры неэлементарных функций
- •§3. Последовательности: основные понятия, примеры
- •I Определение
- •II Элементы поведения и операции
- •III Примеры
- •§4. Бесконечно малые последовательности и их свойства
- •I Два определения
- •II Две эталонные б.М.
- •III Основные свойства
- •§5 Предел последовательности
- •I Три определения
- •II Свойства сходящихся последовательностей и их пределов
- •III Примеры вычисления пределов
- •§6. Бесконечно большие последовательности и их свойства
- •I Два определения
- •II Две эталонных б.Б.
- •III Свойства б.Б. Последовательностей
- •§7. Теоремы о пределах последовательностей
- •§8. Монотонные последовательности. Число
- •I о пределе монотонной последовательности
- •II Число е
- •§9. Предел функции
- •I Общее определение
- •II Частные случаи. Важные понятия
- •III Односторонние пределы
- •IV Теоремы о пределах функций
- •§ 10. Замечательные пределы
- •I Первый замечательный предел
- •II Второй замечательный предел
- •§ 11. Эквивалентные б.М. И б.Б. Функции
- •I Сравнение б.М. И б.Б. Функций
- •II Эквивалентные функции: два определения
- •III Таблица эквивалентностей
- •IV Использование эквивалентностей для вычисления пределов
- •V Асимптотические формулы
- •§12. Понятие непрерывности функции
- •§13. Классификация точек разрыва
- •I Определение
- •II Точка устранимого разрыва
- •III Точка разрыва 1го рода
- •IV Точка разрыва 2го рода
- •§14. Основные свойства непрерывных функций
![]()
Раздел дифференциальное исчисление Тема введение в математический анализ
Лекция 1
§1. Функции одной переменной: основные понятия
I Определение
Рассмотрим две переменные величины xиy. Если по некоторому правилу или закону каждому значению переменной величиныxпоставлено в соответствие одно определенное значение переменной величиныy, то говорят, чтоyесть функция отxи пишут:y=f(x) илиy=y(x).
Используемая терминология: x– аргумент,y– функция;x– независимая переменная,y– зависимая переменная.
В обозначении y=f(x)букваfявляется характеристикой функции и символизирует правило, о котором говорится в определении. Если рассматриваются разные функции, то их характеристики обозначаются разными буквами. И вообще, любая запись видаu=g(v)означает, что переменнаяuесть некоторая функция переменнойv.
II Способы задания функции
Задать функцию означает задать правило (закон) соответствия. Наиболее употребительным является задание этого правила с помощью одной или нескольких формул, содержащих указание на те операции или действия над постоянными числами и над значениями аргумента x, которые необходимо произвести, чтобы получить соответствующее значение функцииy. При этом различают три варианта этого т.н. аналитического способа задания:
явный, например,
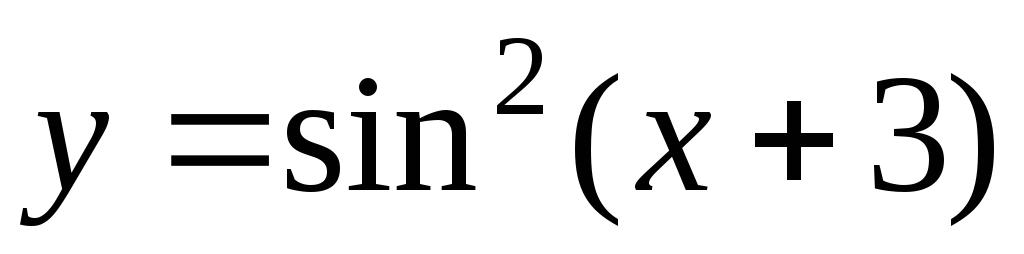 или
или
неявный, например,
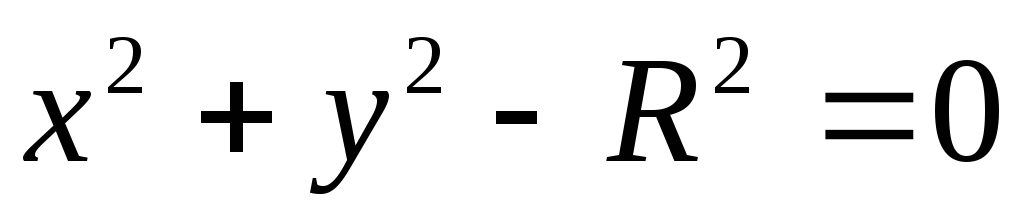 (переменныеxиyсвязаны некоторым уравнением видаF(x,
y)=0);
(переменныеxиyсвязаны некоторым уравнением видаF(x,
y)=0);параметрический, например,
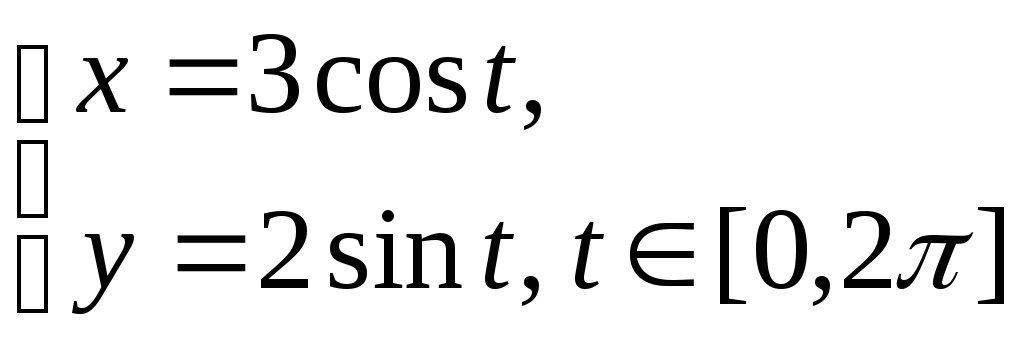 (переменныеxиyзаданы как явные функции вспомогательной
переменной – параметраt).
(переменныеxиyзаданы как явные функции вспомогательной
переменной – параметраt).
На практике часто используют табличныйспособ задания функции, когда задаются таблица отдельных значений аргумента и соответствующих им значений функции. Существуют методы позволяющие вычислить (приближенно!) значения функции, соответствующие промежуточным значениям аргумента, а также подобрать формулу, задающую функцию с определенной точностью.
Весьма распространенным, особенно в экспериментальных науках, является графическийспособ задания функции, при котором соответствие между аргументом и функцией задается посредством некоторой линии в системе координатxOy.
Используют в математике и словесныйспособ задания, когда функция описывается
правилом её составления. Такова, например,
функцияy=[x]:
“![]() естьцелая частьx”,
т.е. наибольшее целое, не превосходящее
числаx.
Наряду с целой частью, рассматривают и
функцию дробная часть числа:{x}=x[x].Примеры:
естьцелая частьx”,
т.е. наибольшее целое, не превосходящее
числаx.
Наряду с целой частью, рассматривают и
функцию дробная часть числа:{x}=x[x].Примеры:
[2,8]=2, [3,4]=4, [2]=2.
III Область определения и область значения функции
Множество D(y) тех значений аргументаx, для которого определены соответствующие значения функцииy=f(x), называютобластью определенияфункции. При нахождении области определения функции, заданной аналитически, необходимо иметь в виду следующее:
если
 ,
то
,
то ;
;если
 ,
то
,
то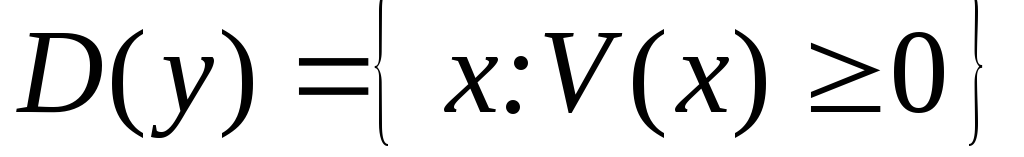 ;
;если
 ,
то
,
то ;
;если
 ,
то
,
то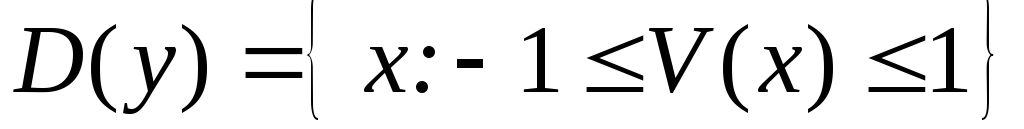 .
.
Множество E(y)тех значений зависимой переменной![]() ,
которые она принимает, когда зависимая
переменная пробегаетD(y),
называютобластью значенийфункции.
,
которые она принимает, когда зависимая
переменная пробегаетD(y),
называютобластью значенийфункции.
Для основных элементарных функций (см. ниже) области значений известны. В общем же случае для нахождения E(y)требуется исследование функции с помощью производных.
