II Частные случаи. Важные понятия

А) Предел на бесконечности ().

Определение 2.

.

Аналогичное определение и для .

Пример 3.,. Рассмотрим. Тогда для последовательности значений функциибудем иметь:, т.к.б.б., аограничена, значит, т.е.. Это означает, что.

Нетрудно убедиться, что и . Для тех функций, для которых, можно писать. Напротив, писатьнельзя, ибо, а.

Геометрическая иллюстрация: конечный предел функции на означает наличие у графика функции горизонтальной асимптоты на(на).

В) Бесконечно малые функции ().

Определение 3.Функциюназывают бесконечно малой (б.м.) в точке(или: при) и пишут «при», если, т .е.

.

Например, в предыдущем пункте мы показали, что при.

Основной результат дает следующая теорема.

Теорема 1.Функцияимеет в точкепределтогда и только тогда, когда разностьесть б.м. при:

при.

С) Бесконечно большие функции ().

Определение 4.Функциюназывают бесконечно большой (б.б.) в точке(при), еслиили, т.е.

 б.б. последовательность опреде-ленного знака.

Все свойства б.м. и б.б. последовательностей остаются справедливыми и для б.м. и б.б. функций. Приведем лишь некоторые из них.

Теорема 2.Для того, чтобы функциябыла бесконечно большой в точкенеобходимо и достаточно, чтобы функциябыла бесконечно малой в этой же точке.

И два свойства.

1) Если при, аограничена в некоторой окрестности точки, то произведениепри.

2) Если б.б. в точке, атакова, что, то произведениеесть б.б. функция при.

Например, в точке, а многочленесть б.б. на, ибо.

Эталонные б.б. и б.м. функции приведем в таблице.

б.м
б.б.

Так же как и б.б. последовательности, б.б. функции можно упорядочить по их порядку роста: при

.

III Односторонние пределы

Рассмотрим функцию . Для произвольной б.м. последовательностиположительных чисел рассмотрим последовательность. Как произведение ограниченной на б.м., она сходится к нулю. Соответствующая последовательность значений функциине имеет предела. Это означает, чтоне существует. Однако,иимеем, а дляи  .

Такая ситуация характерна для многих функций, у которых нет предела в какой-либо точке, что и привело к появлению понятия односторонних пределов.

Определение 5.Пусть

.

Тогда число называют правым пределом (пределом справа или правосторонним пределом) функциив точкеи пишут:или.

Определение левого предела аналогично, только требование заменяют требованием. Обозначения:

или.

Если , то иногда вместопишут. Например,,.

Сформулируем теорему, на которой базируется использование односторонних пределов.

Теорема 3.Для существования пределанеобходимо и достаточно существования порознь и равенство односторонних пределов:.

IV Теоремы о пределах функций

Теорема 4.Пусть у функциисуществует. Тогда в некоторой окрестности точки(за исключением, быть может, самой точки). Более того,.

Теорема 5.Пусть у функциисуществует конечный предел при. Тогда в некоторой окрестности точкифункцияограничена.

Теорема 6. Функцияимеет предел в каждой точке числовой прямой, причем.

Теорема 7 (операции над пределами). Пусть функциииимеют в точкеконечные пределыисоответственно. Тогда в этой точке имеют конечные пределы и функции: 1); 2); 3); 4); 5)(при). При этом имеют место следующие равенства:

,

(здесьсимвол арифметической операции).

Для доказательства рассмотрим произвольную последовательность значений аргумента, сходящуюся к.

В силу существования пределов функций исоответствующие последовательности значений функцийиимеют пределыи. Тогда, используя теорему 2 §7, получим, что последовательностьсходится к. Согласно определению предела функции это означает, что.

Теорема 8 (предельный переход в неравенствах).Пусть функциииимеют в точкеконечные пределы и в некоторой окрестности этой точки (за исключением, быть может, самой точки). Тогда и. В частности, если(), то и().

Теорема 9.Еслии в некоторой окрестности точки(за исключением, быть может, самой точки), то.

Теорема 10 (о замене переменной).Пусть хотя бы одна из функцийилиявляется строго монотонной и пусть существуют пределыи. Тогда и у сложной функции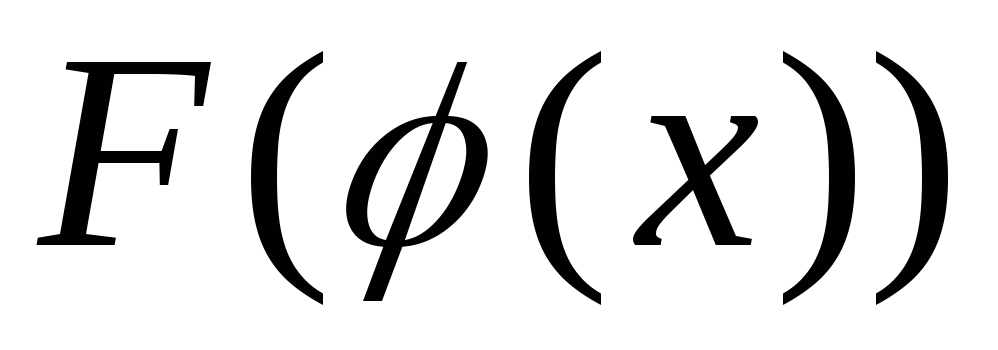существует предел в точке, причем

.

Теорема 11 (пределы элементарных функций).Пустьэлементарная функция и точкавместе с некоторой окрестностью. Тогда(в силу непрерывности элементарных функций).

Теорема 12.Всякая ограниченная монотонная на промежутке функция имеет в каждой точке промежутка конечные односторонние пределы.

Пример 4.

,

.

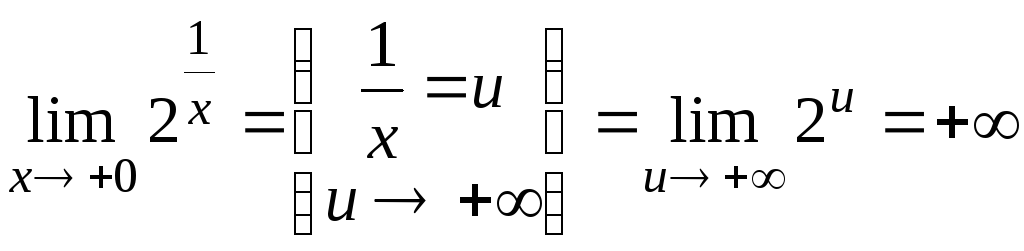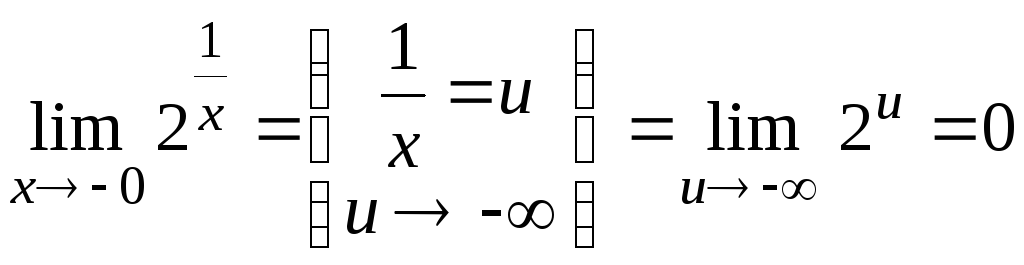Пример 5.

а) ; б).

Путем деления числителя и знаменателя на самое быстрорастущее слагаемое, перейдем от б.б. функций к б.м. функциям и получим результат:

а) ;

б) .

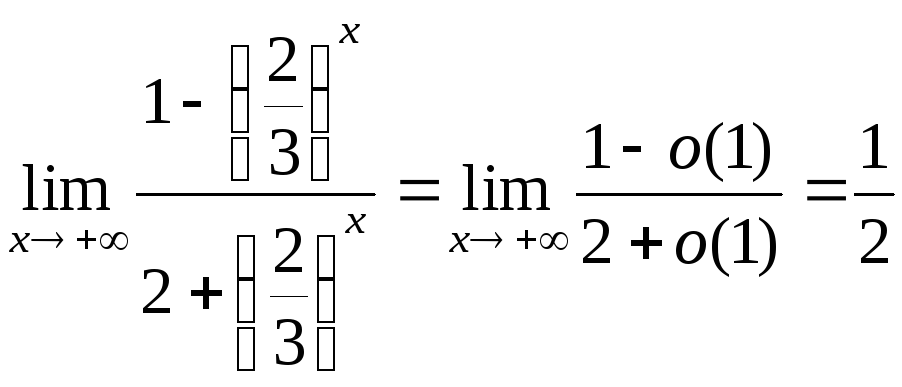Замечание.Кроме определения предела функции на «языке последовательностей», существует (равносильное) определение предела функции на т.н. «языке». Некоторые из теорем о пределах удобнее доказывать именно на этом языке.