Тема исследование функций с помощью производных

Лекция 12

§1. Условие постоянства функции

Теорема. Если функция непрерывна на промежуткеи во всех внутренних точках отрезка , топостоянна на этом промежутке.

Доказательство. Пусть . Применим теорему Лагранжа к функции на промежутке :. Но по условию, следовательно, и поэтому(на правом концев силу непрерывности).

Пример. Рассмотрим функцию на промежутке . Её производная:

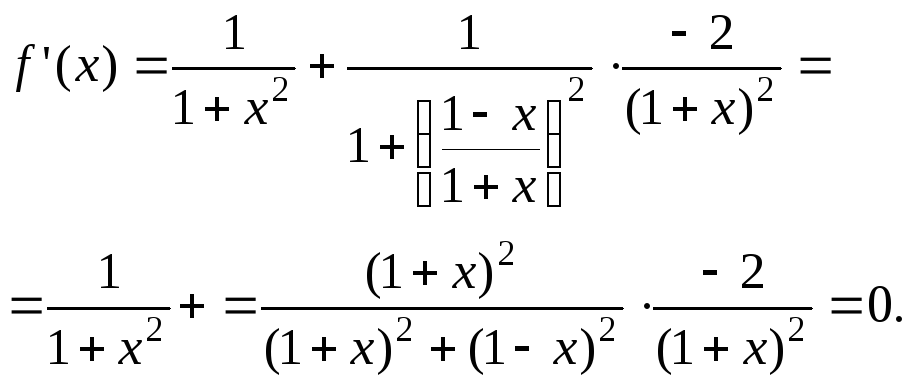
Следовательно, const на . Чтобы найти эту константу, достаточ-но вычислитьв любой точке, например,. Итак, мы доказали тождество .

В интегральном исчислении важное приложение найдет следствие, вытекающее из доказанной теоремы.

Следствие. Если функцииинепрерывны на промежуткеи имеют равные производные во всех внутренних точках промежутка, то эти функции всюду в отличаются лишь на постоянную:.

Для доказательства достаточно применить теорему к вспомогательной функции . Тогдаи.

§2. Условие монотонности функции

Известно, что функция называется строго возрастающей на , если для любых точекиз неравенстваследует неравенство. Другими словами знак приращения функции совпадает со знаком приращения аргумента:. Для убывающей функции, естественно,.

Теорема. (Достаточное условие монотонности). Пусть функция дифференцируема на . Тогда:

1) если на ,то строго возрастает на ;

2) если на ,то строго убывает на .

Доказательство. Возьмём две произвольные точки , причём пусть . Применим теорему Лагранжа к функции на промежутке(условия теоремы выполнены, ибо непрерывностьвытекает из её дифференцируемости):По предположению , следовательно,знак определяется знаком производной. 1) Если, то ии; т.к. это верно для любых, товозрастает на . 2) Если , то ии, что означает убывание.

Замечание. Связь между знаком и направлением изменениягеометрически очевидна, если вспомнить, что производная – это угловой коэффициент касательной к графику. Однако, даже у строго монотонной функциикасательная может быть и горизонтальной, т.е.для отдельных значенийможет обращаться в0. Примером служит функция : она строго возрастает, но производнаяприобращается в ноль.

Итак, теорема сводит вопрос о возрастании (убывании) функции к решению неравенства().

Пример. Исследовать на монотонность функцию . Находим производную и разлагаем её на множители:. Метод интервалов позволяет определить знак:

-

На интервалах ифункция возрастает, а на– убывает.

§3. Исследование функции на экстремум

Напомним уже известные факты. Во-первых, точка экстремума – это всегда внутренняя точка области определения функции; она характеризуется тем, что знак приращения функции не зависит от знака приращения аргумента, если последнее достаточно мало. Во-вторых, необходимое условие экстремума даётся теоремой Ферма: если в точке экстремума функция дифференцируема (т.е. обладает конечной производной), то производная в этой точке равна 0.

Точки, в которых производная функции обращается в ноль, принято называть стационарными точками.

Однако, если рассматривать функции, не имеющие в отдельных точках конечной двусторонней производной, то не исключена возможность, что экстремум придётся на какую на какую-либо из таких точек. Например, функции иимеют вминимумы, в тоже время,и,.

Определение. Точку называют критической точкой первого порядка функции, еслиили не существует.

Из теоремы Ферма следует, что точки экстремума следует искать среди критических точек (их ещё называют точками возможного экстремума). Требуется дополнительное исследование таких точек, чтобы отобрать среди них точки экстремума. Это исследование выполняется с помощью достаточных условий экстремума.

Теорема 1 (первое достаточное условие экстремума). Пусть – крити-ческая точка первого порядка непрерывной функциии пусть существуеттакое, что в односторонних окрестностях этой точки:и– функциядифференцируема и её производная сохраняет знак. Тогда:

1) если вив, то– точка максимума;

2) если вив, то– точка минимума;

3) если одного знака ви, то в точкенет экстремума.

Доказательство. 1) Возьмём произвольные точки ии рассмотрим функциюна двух промежутках:и. На каждом из этих промежутков функцияудовлетворяет условиям теоремы Лагранжа, следовательно, существуют точкиитакие, что:

,

.

Из этих неравенств вытекает, что и. Таким образом значение – самое большое среди значенийдля. Это и означает:– точка максимума.

2) Доказывается аналогично.

3) Если , товозрастает как в, так и в. Если же, тоубывает в тех же окрестностях. В обоих случаях такое поведение функции говорит о том, что в точкеу неё нет

экстремума.

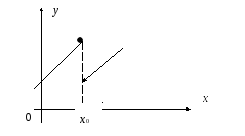
Замечание 1. Требование непрерывности функции нельзя ослабить, о чем свидетельствует рисунок: в точке функция имеет максимум, в то же время при переходе через эту точку производная не меняет знак.

Замечание 2. Доказанную теорему не всегда можно применить, ибо для некоторых функций требование сохранения знака производной не выполняется. Например, для функции

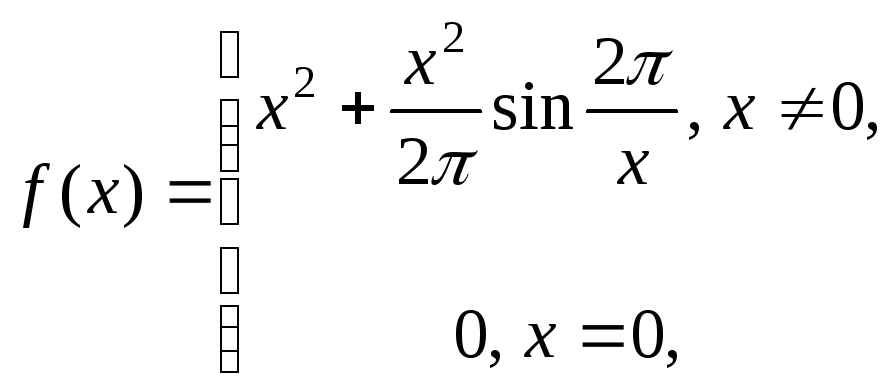
имеем:

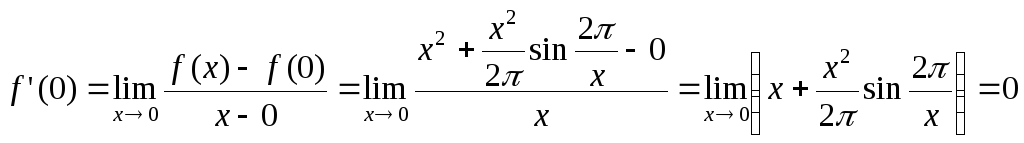, значит, точка 0 – критическая точка. Далее, для

Выражение в скобках ограничено, поэтому при близких к нулю первый член полученной разности также близок к нулю, а второй член принимает значения от –1 до +1. Значит, знакопределяется членом. Но в точках видаэтот член обращается в ноль и меняет знак. А так как при , то в любой сколь угодно малой окрестности нуля бесконечное число раз меняет знак.

Теорема 2 (второе достаточное условие экстремума). Пусть функция имеет в критической точкеконечную вторую производную. Тогда:

1) если , то– точка минимума;

2) если , то– точка максимума;

3) если , то требуется дополнительное исследование.

Доказательство. Существование конечной производной означает, что существует конечная производнаяв некоторой окрестности точкии, ибо– критическая точка. Обозначим. Тогда условия теоремы означают, что существует конечный предел

.

Пусть, например, . Тогда дляблизких ки, то есть . Это означает, что функция возрастает в некоторой окрестности точки. Но. Следовательно, левее точкифункцияотрицательна, а правее – положительна. Однако,. Значит, первая производная данной функции при переходе через точкуменяет знак с «–» на «+». Это означает, что точка– точка минимума. Аналогично рассматривается и случай. В необходимости дополнительного исследования, когда, убеждают две функции:и. Очевидно, что– точка0 критическая для обеих функций, и . Однако, дляноль – это точка минимума, ав нуле не имеет экстремума.

Замечание 3. В теме «Формулы Тейлора и Маклорена» будет сформулировано и доказано третье достаточное условие экстремума, с помощью которого и производится это дополнительное исследование.

Пример 1. Найти точки экстремума функции .

Решение. Раскроем знак модуля и вычислим производную:

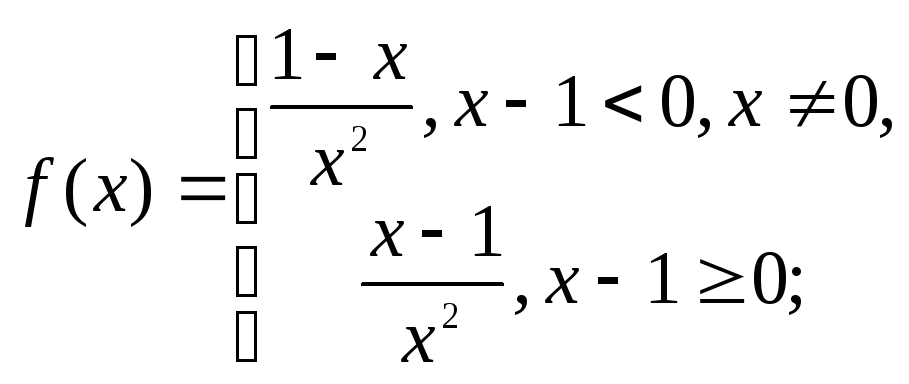
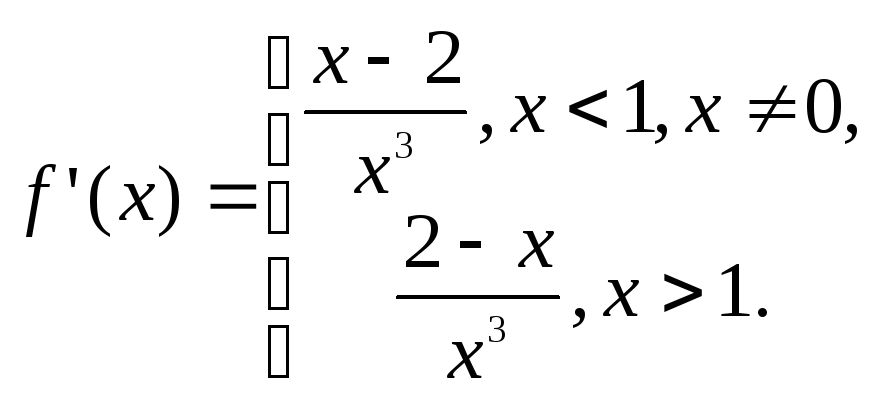
Наличие модуля в выражении для может привести, и в нашем случае приводит, к несуществованиюв точке, где модуль обращается в ноль. Действительно,

Отличие левой производной от правой и означает отсутствие производной в точке , т.е. эта точка – критическая. Другие критические точки – это нули производной:

Итак, имеем две критические точки Они разбивают область определения функциина интервалы знакопостоянства производной, т.е. на интервалы монотонности функции. Для определения знакана интервале достаточно определить этот знак в какой-либо точке интервала. Дальнейшее исследование удобно вести, нарисовав вспомогательный чертёж:

Еще раз напомним, что критические точки наносятся на область определения. Мы получаем 4 интервала. Определяем знаки :

Анализ чертежа показывает: в точке функция имеет локальный минимум, причём, а в точке– локальный максимум:.

На чертеже видны и интервалы монотонности : наифункция возрастает, а наи– убывает.

Замечание 4. В точке максимума рассмотренная функция имеет нулевую производную и касательная к графику функции – горизонтальна. О таком максимуме говорят «гладкий максимум» (аналогично «гладкий минимум»). В противоположность этому, точкаявляется точкой «негладкого минимума» – в этой точке производная не существует, хотя есть односторонние производные. Соответствующая точка графиканазываетсяугловой точкой графика.

Пример 2. Найти экстремумы функции .

Решение. – существует везде.

–точка максимума;

–точка минимума;

–точка минимума.

Лекция 13