§5. Асимптоты графика функции

Если функция имеет бесконечные разрывы или определена на бесконечном промежутке, то в силу конечности размеров чертежа приходится довольствоваться лишь частью всего графика. Асимптоты позволяют отчетливо представить себе вид графика и за пределами чертежа.

Будем говорить, что точка удаляется в бесконечность, если расстояниеот точки до начала координат неограниченно увеличивается.

Определение. Прямая называется асимптотой линии, если расстояние от текущей точкилиниидо прямойстремиться к нулю по мере удаления точкив бесконечность.

Расстояние может стремиться в бесконечность различными способами: 1); 2); 3),. В зависимости от способа и различают вертикальные, горизонтальные и наклон- ные асимптоты.

I Вертикальные асимптоты

Прямая является вертикальной асимптотой графика функции, если хотя бы один из односторонних пределов функции в этой точке равенили(т.е. точка– точка бесконечного разрыва).

Примеры.

1. График функции имеет асимптоту, ибо

, .

2. Для графика логарифмической функции ось ординат является^{асимптотой, ибо} .

3. Рассмотрим функцию . Для неё имеем:

^{прямая x=0 – вертикальная асимптота}.

Отметим, что график функции может иметь любое число вертикальных асимптот. График же элементарной функции не может пересекать свою вертикальную асимптоту

II Горизонтальные асимптоты

Прямая является горизонтальной асимптотой графика функциипри, если.Примеры.

4. Для графика показательной функции ось абсцисс является асимптотой при, если, и при, если.

5. Для графика прямая– асимптота при, а прямая– асимптота при.

6. Для функции :, значит, для этой функции ось абсцисс – асимптота и при, и при.

Отметим, что график элементарной функции может иметь не более двух асимптот: по одной на каждой из бесконечностей. Кроме того, график может пересекать свою горизонтальную асимптоту (см. пример 6).

III Наклонные асимптоты

Теорема. Для того, чтобы график функции имел принаклонную асимптоту, необходимо и достаточно, чтобы существовали конечные пределы

и .(1)

Доказательство. Запишем уравнение прямой в формеТогда можно воспользоваться готовой формулой для рас-стояния от точки графикадо прямой:

.

Напомним ещё два результата из теории пределов:

ибо

Докажем необходимость. Пусть – асимптота. Значит,при, т.е.Отсюда сразу имеем. С другой стороны

поэтому, , а т. к., то иЭто же означает, что.

Докажем достаточность. Пусть существуют пределы (1). Тогда: По определению это и означает, что прямая, гдеиопределены формулами (1), является асимптотой. Теорема доказана.

Замечание 1. Аналогично определяется наклонная асимптота для случая . Наклонных асимптот у графика элементарной функции может быть не более двух, причём горизонтальная асимптота – это частный случай наклонной. График может пересекать свою наклонную асимптоту.

Примеры.

7. Найдём асимптоты графика функции .

–асимптота при ,

нет горизонтальной асимптоты при , но может быть наклонная:

Итак, прямая – наклонная асимптота графика функциипри.

Заметим, что вертикальных асимптот график не имеет, ибо данная функция является непрерывной ( в силу элементарности ) на всей числовой оси.

8. Найти асимптоты графика функции Очевидно, что гори-зонтальных асимптот нет, ибоДалее,

.

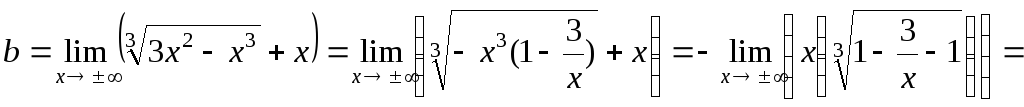
Прямая – наклонная асимптота графика функцииприи при.

Замечание 2. Нетрудно заметить, что, если при(), то прямая– наклонная асимптота графика функции при().

Пример.

9.

Так как то прямая– асимптота графика прии.

Задача. Найти асимптоты графика функции

Лекция 14