§4. Разложение по формуле Маклорена некоторых элементарных функций

I. .

Поскольку и , то формула Маклорена имеет вид

^{где: 1)}

²⁾ , для любого промежутка (очевидно, что ).

II. .

^{Известно, что Тогда:}

Условия теоремы из §3 выполнены на всей оси с Формула Маклорена имеет вид

^{где: 1)}

2) .

На первый взгляд написанные формы для отличаются от общих результатов. Но надо не забывать, что, вообще говоря, в разложении для можно дописать ещё один член с , только коэффициент при этой степени равен 0.

III. .

Аналогично предыдущему нетрудно получить

где: 1)

^{2) .}

IV. .

Прежде всего, имеем . Теперь можно использовать формулу дифференцирования степенной функции:

При Формула Маклорена имеет вид (с учётом того, что ):

где: 1)

2)

Отметим, что для оценки остаточного члена для требуется форма , отличная от формы Пеано и Лагранжа. Кроме того, пользоваться разложением в приближённых вычислениях можно только для : ^{только для таких значений} .

V. .

Поскольку

то

Формула Маклорена для этой функции имеет вид:

Здесь для остаточного члена имеем: Как и в случае логарифмической функции для оценки требуется форма, отличная от Пеано и Лагранжа. Более подробно об этом мы будем говорить в третьем семестре в теме «Степенные ряды». Отметим только, что написанным разложением в приближённых вычислениях можно пользоваться лишь для .

VI. Другие функции. Пользуясь известными разложениями, можно, не вычисляя производных, непосредственно писать разложения с остаточным членом в форме Пеано и для более сложных функций. При этом все степени х, до назначенной включительно, учитываем точно, а более высокие степени будем сразу включать в (не выписывая их).

Пример 1. Написать разложении функции до .

В силу I имеем:

где остаточный член

, так как . Далее, в силу II имеем: . Таким образом

После упрощения получим искомое разложение

Пример 2. Написать разложение функции до члена с .

Согласно IV,

.

Необходимое разложение для (см. III) выпишем в нескольких вариантах:

.

Учитывая, кроме всего, и ~–0,5х², х→ 0, получим:

После приведения подобных членов будем иметь:

.

§5. Приложения формулы Маклорена

I Вычисление пределов

В §11 темы «Введение в математический анализ» были приведены т.н. асимптотические формулы (ещё говорят «асимптотические оценки») такие, как: (при ) и т.п. Фактически они являются частными случаями формул Маклорена для соответствующих функций. Для вычисления простых пределов тех формул было достаточно. Однако, при работе со сложными пределами требуются формулы Маклорена более высокого порядка. Например, предел

при помощи формулы вычислить невозможно, ибо

Если же возьмём для формулу Маклорена третьего порядка , легко получим

Рассмотрим более сложные примеры.

Пример 1. Вычислить предел

Для вычисления используем такие формулы:

, где

Имеем:

.

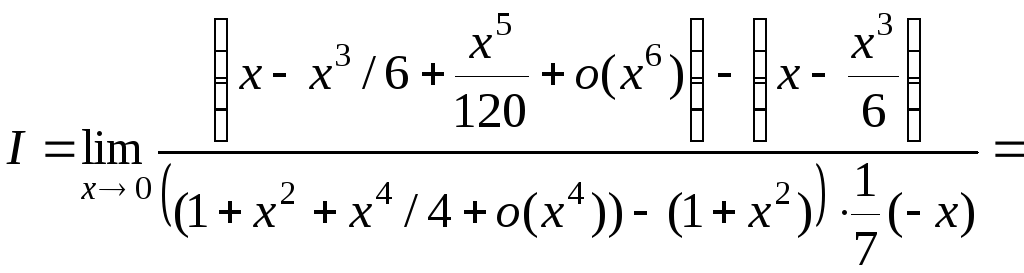
Пример 2. Часто студенты считают, что при

.

Докажем по определению, что это не так.

Действительно,

Вычислим отдельно предел показателя степени, используя формулу Маклорена с при:

Используя непрерывность показательной функции, можем записать: . Полученный предел отличен от 1, это и означает, что предполагаемая эквивалентность неверна.