§4. Исследование функции на выпуклость и перегиб

I Направление выпуклости (вогнутости)

Пусть функция дифференцируема на интервале. Дифференцируемость означает существование конечной производной, что, в свою очередь, означает наличие у графика функции невертикальной касательной. А для такой прямой есть понятия «выше» и «ниже».

Определение 1. Дифференцируемая функция называется выпуклой вниз (вверх) на интервале, если её график лежит не ниже (не выше) любой касательной к графику функции на.

Говорят ещё: «график функции направлен выпуклостью вниз (вверх)». Вместо «выпукла вниз (вверх)» говорят иногда «вогнута вверх (вниз)». Ещё вместо «выпуклая вверх» говорят просто «выпуклая», а вместо «выпуклая вниз» – «вогнутая».

На рисунке слева изображен график функции выпуклой вниз, а справа – вверх.

Теорема 1 (первое достаточное условие выпуклости). Пусть функция имеет на интервалеконечную производную второго порядка. Тогда:

1) если на, тонаправлена выпуклостью вниз;

2) если на, тонаправлена выпуклостью вверх.

Доказательство. Обозначим: – ордината точки графика функции с абсциссой;– ордината точки касательной к графику с той же абсциссой. Если– произвольная точка из, то уравнение касательной к графикув точке с абсциссойимеет вид:. Составим разность ординат:. Существованиеозначает, что существует (и непрерывна)и, следовательно,– непрерывна. Тогда к функциина промежуткеприменима теорема Лагранжа:

Тогда

Функция непрерывная и дифференцируемая, значит, к ней можем приме-нить теорему Лагранжа на промежутке

Итак, для разности ординат точки графика и точки касательной имеем равенство: . Возможны два случая взаимного расположения точек:

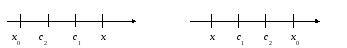
В обоих случаях произведение положительно, следовательно,: если, то, т.е. график расположен выше касательной, функция выпукла вниз; если, то, график расположен ниже касательной, функция выпукла вверх. Теорема доказана.

Замечание 1. Доказанная теорема имеет простую геометрическую иллюстрацию. Если функция выпукла вниз, то угловой коэффициент касательной, т.е. возрастает, значит. Для выпуклой вверх функции первая производная убывает, значит, вторая производная отрицательна.

Пример 1. Исследовать на выпуклость степенную функцию

Имеем . Еслиили, то, а если, то. Значит,на лучевыпукла вниз прии, и выпукла вверх при. Приилиимеем линейную функциюили. Такие функции могут считаться как выпуклыми вверх, так и выпуклыми вниз.

II Точки перегиба

Определение 2. Точку называют точкой перегиба графика функции, если она отделяет участки графика с противоположными направлениями выпуклости.

Одно полезное свойство точки перегиба: если в точке перегиба существует касательная к графику функции, то она пересекает график.

Замечание 2. Часто это свойство принимают за определение точки перегиба. Но такое определение вовсе не равносильно данному выше. Кривая может и не иметь касательной в точке перегиба, а может случиться обратное: кривая пересекает касательную в точке, которая не отделяет участки с противоположными направлениями выпуклости. Примерами могут служить

функции и: у первой в точках перегибаинет касательных (хотя есть односторонние касательные), для графика второй прямыеиявляются касательными.

Можно привести и более интересный пример:

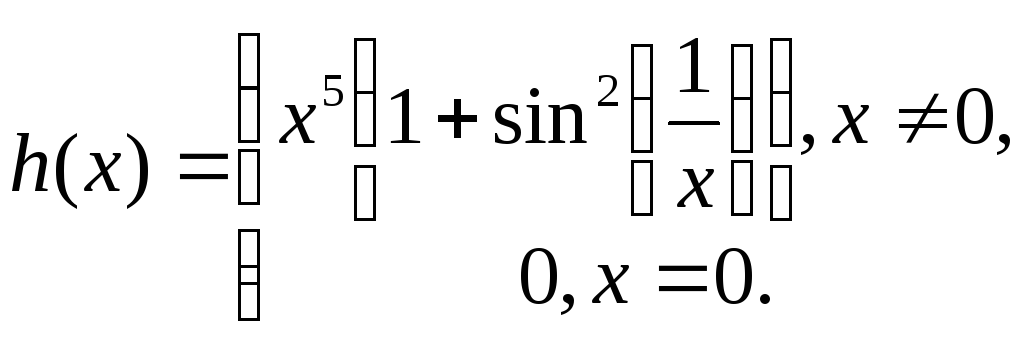
График этой функции в начале координат касается оси и пересекает её; здесь существует непрерывная вторая производная, но она бесконечное множество раз меняет знак в окрестности нуля. (Предоставляем читателю самому провести все необходимые вычисления для этих функций).

Приведём без доказательств ряд теорем, в которых используется понятие критической точки второго порядка.

Определение 3. Точка называется критической точкой второго порядка функции, если вторая производная функции в этой точке равна нулю или не существует.

Теорема 2 (необходимое условие точки перегиба). Если – точка перегиба функции, то– критическая точка второго порядка.

Теорема 3 (первое достаточное условие точки перегиба). Пусть – критическая точка второго порядка непрерывной функциии пусть существуеттакое, что в окрестностяхивторая производнаясуществует и имеет противоположные знаки. Тогда точка– точка перегиба графика функции.

Теорема 4. (второе достаточное условие точки перегиба). Если функция имеет в точкеконечную производную третьего порядка и удовлетворяет условиям,, то график этой функции имеет перегиб в точке.

Пример 2. Найти интервалы выпуклости и точки перегиба функции .

Решение. В предыдущем параграфе мы уже исследовали эту функцию на экстремум и получили

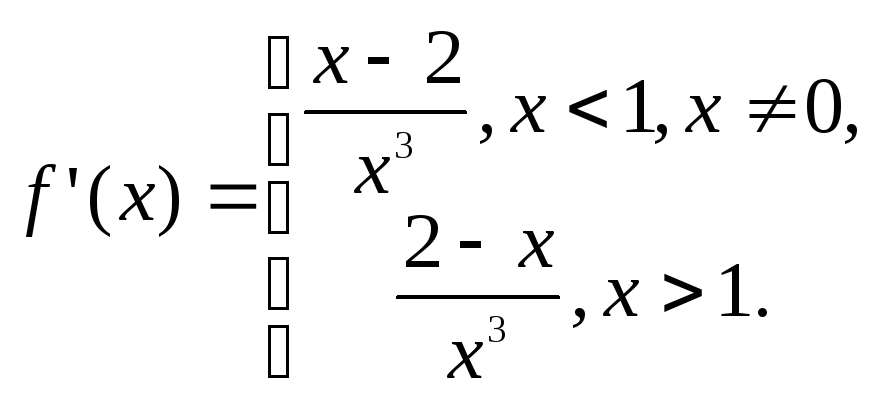
Находим вторую производную:

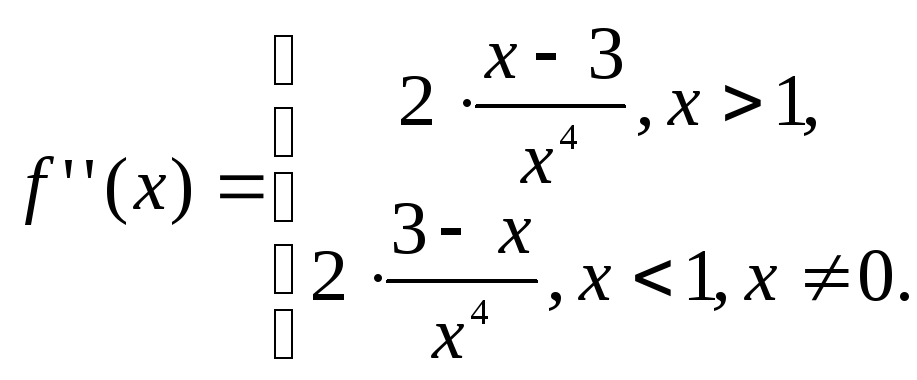
Напомним, что не существует в точке, значит, ине существует в этой точке, т.е. эта точка – критическая точка второго порядка. Ещё одну такую точку найдём, решив уравнениеЭти критические точки разбивают область определенияна интервалы знакопостоянства второй производной, т.е. интервалы выпуклости самой функции. Знакиопределяем так же, как и знакипри исследовании на экстремум. Приходим к чертежу:

Итак, имеем: на интервалах ,ифункция выпукла вниз, а на– выпукла вверх; точкии– точки перегиба.

Замечание 3. В случае недифференцируемой функции принято другое определение выпуклости, а именно: функция называется выпуклой вниз (вверх) на интервале, если все точки любой дуги её графика лежат под (над) соответствующей хордой или на ней. Для дифференцируемой функции это определение равносильно данному выше.

Замечание 4. Третье достаточное условие перегиба будет дано в следующей теме.