§4. Бесконечно малые последовательности и их свойства

I Два определения

Определение 1 (язык «N»). Последовательностьназывают бесконечно малой (б.м.), если для любого (сколь угодно малого) положительного числанайдется номерN=N()(зависящий, вообще говоря, от) начиная с которого выполняется неравенство.

Используя квантор всеобщности и квантор существования, это определение можно записать следующим образом:

.

Для дальнейшего нам понадобится одно важное понятие. Вот его определение:

интервал вида называется-окрестностьюточки.

Неравенство , фигурирующее в определении 1, равносильно двойному неравенству, что означает следующее:. Теперь можем дать второе определение (равносильное первому).

Определение 2 (язык «окрестностей»). Последовательностьназывается б.м., если любая (сколь угодно малая)-окрестность нуля содержит все члены последовательности, начиная с некоторого номераN()(зависящего, вообще говоря, от).

Из определения 2 можно сделать вывод: внелюбой (сколь угодно малой) -окрестности нуля содержится лишь конечное число членов б.м. последовательности.

Для б.м. последовательности принято обозначение(читается «о малое от 1»), иногда уточняют, добавляя:n.

II Две эталонные б.М.

1) при > 0. Примеры:.

2) при . Примеры:.

Доказательство первого утверждения

Возьмем и зафиксируем число . Надо найти номер, начиная с которого

.

В качестве номера можно взять, ибо еслит.е.и получаем. Так. как такой номер можно найти, то тем самым доказана бесконечная малость последовательности.

Второе утверждение доказывается аналогично, только для решения показа-тельного неравенства используются логарифмы.

III Основные свойства

Эти свойства нужны для того, чтобы доказывать бесконечную малость последовательности, не применяя определения (1 или 2).

1. Пусть 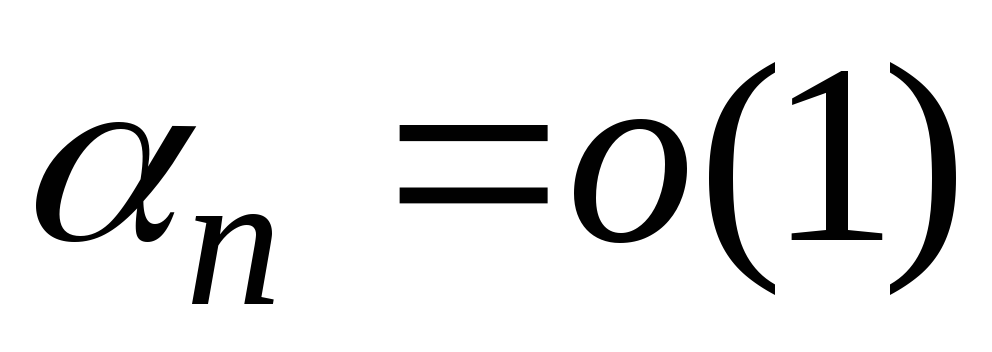Тогда:

а) – ограничена;

б) ;

в) ;

г) ;

д) если или, то.

2) Произведение ограниченной последовательности на бесконечно малую есть бесконечно малая.

3) Сумма, разность и произведение б.м. есть б.м.

Для доказательства 1а) возьмем конкретное , например,= 1. Тогда. Вне интервала (1,1) могут находиться лишь конечное число членов, т.е.. Т.к. в конечном множестве чисел есть наибольшее и наименьшее, то все членынаходятся междуи, т.е.ограничена.

Докажем свойство 2. Пусть , аограничена, т.е.. Для доказательства того, чтонеобходимо взять произвольноеи найти номер, начиная с которого. Итак, пустьпроизвольное, рассмотрим число. Т.к., то для этого. Тогда имеем:

,

т.е., начиная с имеем, следовательно.

Примеры использования.

а) , т.к., аэталонная б.м.

б) , т.к.и, аограниченая.

в) Т.к. для, то. Следовательно.

Замечание.Частное двух б.м. может быть каким угодно.

Задачи(для самостоятельного решения).

1. Пусть . Следует ли отсюда, чтоили?

2. Может ли среди членов б.м. последовательности быть бесконечно много

одинаковых членов? Если да, то каких?

Лекция 3

§5 Предел последовательности

I Три определения

Определение 1.Числоназывают пределом последовательностии пишут, если последовательностьесть бесконечно малая.

Используя определение 1 предыдущего параграфа, можно дать еще и такое определение предела.

Определение 2 (язык «»).Числоназывают пределом последова- тельности, если

.

Последнее неравенство с модулем равносильно двойному неравенству или. Другими словами,. Получаем еще одно определение предела.

Определение 3 (язык «окрестностей»). Числоназывают пределом последовательности, если любая (сколь угодно малая)-окрестность числасодержит все члены последовательности, начиная с некоторого номера, другими словами, вне такой окрестности содержится лишь конечное число членов последовательности.

Замечания.

1. Из определений следует, что и, если.

2. Если для последовательности существует предел (в указанном выше смысле), то она называетсясходящейся. В противном случае последовательность называетсярасходящейся. Примерами расходящихся последовательностей могут служить:.

3. Определению 1 можно придать другую форму, более удобную в некото-рых случаях:

, гдепри.

Такая форма позволяет найти предел такой, например, последовательности:

.

4. (если существует) не зависит от любого конечного числа членов последовательности.