§9. Касательная плоскость к поверхности

Рассмотрим уравнение с тремя переменными . В координат-ном пространстве оно определяет некоторую поверхность ().

Определение 1. Точка называется обыкновенной, если в этой точке существуют конечные производные, причем они не обра-щаются в ноль одновременно. В противном случае точка называется особой.

Определение 2. Прямая линия называется касательной прямой к поверх-ности () в ее обыкновенной точке, если она является касательной к некото-рой линии, лежащей на () и проходящей через точку.

Теорема. Все касательные прямые к поверхности в ее обыкновенной точке лежат в одной плоскости.

Доказательство. Пусть линия

лежит на данной поверхности ():и проходит через ее точку. Это означает следующее:

1) ;

2) существует значение такое, что.

Продифференцируем тождество из пункта 1): ≡ 0.

Рассмотрим этот результат в точке :

Левая часть последнего равенства – это скалярное произведение направляющего вектора касательной к линии в точке

и вектора

,

проекции которого определяются лишь поверхностью () и ее точкой, и не зависит от линии. Но равенствоозначает, что, т.е.все каса-тельные прямые к () в ее точкеперпендикулярны вектору. Это же, в свою очередь, означает, что все эти прямые лежат в одной плоскости иесть нормаль-ный вектор этой плоскости. Теорема доказана.

Определение 3. Плоскость, в которой лежат все касательные прямые к поверхности в ее обыкновенной точке, называется касательной плоскостью.

Уравнение касательной плоскости к поверхности ():в ее обыкновенной точкеимеет вид

В случае явного задания поверхности ():уравнение касательной плоскости таково:

.

Определение 4. Прямая, проходящая через точку поверхности () и перпендикулярная касательной плоскости, называется нормалью к поверхности.

Уравнения нормали (канонические):

Пример. К поверхности ():провести касательную плоскость, параллельную плоскости:.

Решение. Нормальный вектор касательной плоскости составлен из частных производных функции , вычисленных в точке касания:

Так как , тои, следовательно, т.е

Таким образом, точка касания такова: Нозначит ее координаты удовлетворяют уравнению ():

.

Отсюда иИмеем две точки касания (и две касательные плоскос-ти):

и .

Уравнения касательных плоскостей

и .

После упрощения получим:

и .

Приведем ряд задач для самостоятельного решения.

1. Дана поверхность ():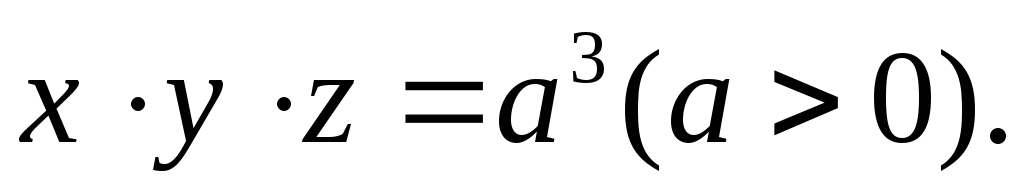Доказать, что любая каса-тельная плоскость к () образует с координатными плоскостями тетраэдр постоянного объема.

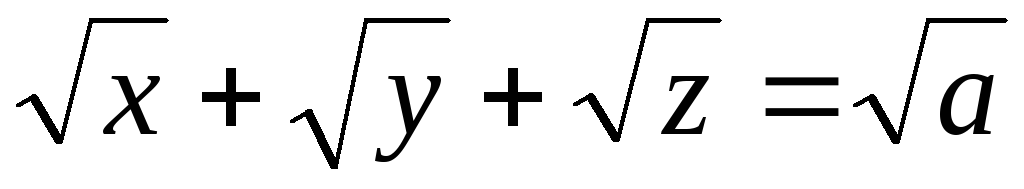2. Дана поверхность ():. Доказать, что любая касса-тельная плоскость к () отсекает от координатных осей отрезки, сумма длин которых постоянна.

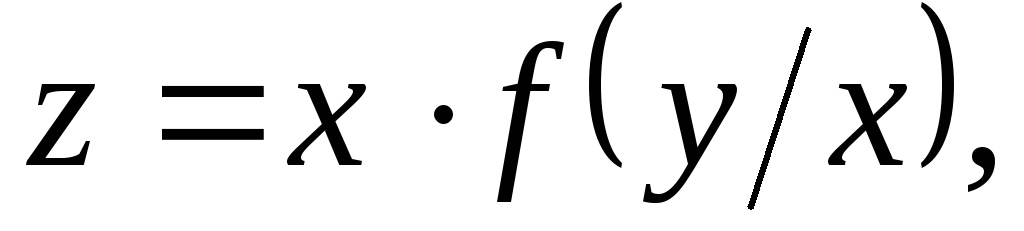3. Дана поверхность ():где– дифференцируемая функция. Доказать, что все касательные плоскости к () пересекаются в одной точке.

Лекция 20

§10. Производные высших порядков

Если функция имеет частные производныевкаждой точке некоторой области , то они представляют собой функции двух переменных, определенные в. Может случиться, что эти функции имеют в

частные производные. Тогда эти производные называются частными производ-ными второго порядка

,,,.

Используются и другие обозначения, например:

, .

Производные иназываются смешанными производными второго поряд-ка. При некоторых условиях смешанные производные не зависят от порядка диф-ференцирования.

Теорема. Пусть функция имеет в областичастные производные. Пусть, кроме того, смешанные производныеинепре-рывны в. Тогда имеет место равенство

= .

Аналогично производным второго порядка вводятся частные производные третьего, четвертого, …, -го порядка. Для смешанных производных высших по-рядков остается справедливой сформулированная выше теорема.