§5. Дифференцируемость и полный дифференциал

Напомним, что полным приращением функции в точке

называют разность

Определение 1. Функция называется дифференцируемой в точке, если ее полное приращение в этой точке может быть представлено в виде:

где А, В – некоторые числа, независящие от , аα и β – бесконечно малые при

Теорема 1. Если функция дифференцируема в точке, то: 1) она непрерывна в этой точке; 2) она имеет в этой точке конечные производ- ные, причем.

Доказательство первого утверждения сразу следует из (1) и замечания к §3. Для доказательства второго утверждения положим в (1) тогдаРазделив обе части равенства наи устремляяк нулю, получим:

т. е.

Аналогично доказывается и

В отличие от функций одной переменной (для которых дифференциру-емость равносильна существованию конечной производной), для функций нескольких переменных из существования частных производных не следует непрерывность и дифференцируемость. Это доказывается следующим примеров.

Пример. Рассмотрим функцию

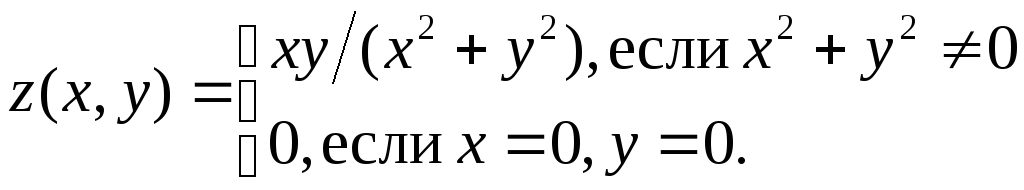
Вычислим производную по в начале координат:

.

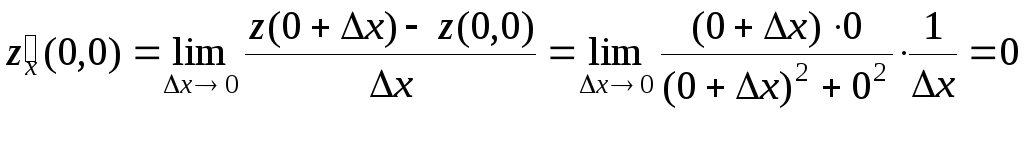Аналогично В то же время эта функция не является непрерывной (а следовательно, является недифференцируемой) в начале координат, ибо ее предел в этой точке не существует (см. пример 2§3).

Таким образом, функция имеет конечные производные в точке, но не является непрерывной в этой точке. Эта ситуация связана с тем, что существование частных производных в точкеопределяется поведением функции на прямыха непрерывность зависит от поведения функции во всей окрестности точкиМ₀.

Примем без доказательства теорему, устанавливающую достаточные усло-вия дифференцируемости.

Теорема 2. Если функция имеет частные производные в некото-рой окрестности точки и эти производные непрерывны в самой точке, то функция дифференцируема в точке.

Определение 2. Главная часть полного приращения дифференцируемой функции, линейная относительно приращений аргументов, называется полным дифференциалом функции и обозначается символом :

Если договорится считать дифференциалами независимых переменных их приращения, то формула (2) примет вид:

Обозначим: это расстояние между точкамии. Очевидно, что стремлениек нулю равносильно одновременному стремлению к нулю приращенийи. Формулу (1) можно теперь переписать в виде

Отсюда при малых иполучим приближенную формулу

,

которая используется в приближенных вычислениях.

Замечание. С геометрической точки зрения, дифференцируемость функции вточке означает наличие касательной плоскости к графи-ку функции в точке(см. ниже §8).

§6. Производные сложных функций

Приведем без доказательства ряд формул дифференцирования сложных функций. Все встречающиеся функции одной или нескольких переменных считаем дифференцируемыми.

1. Если то

2. Если , ато для сложной функции одной переменнойz(u(x),v(x)) имеем

или используя другие обозначения,

В частности, если а, то

В этом случае производную называют полной производной, в отличие от– частной производной.

3. Если , аи, то для сложной функции двух переменныхимеем:

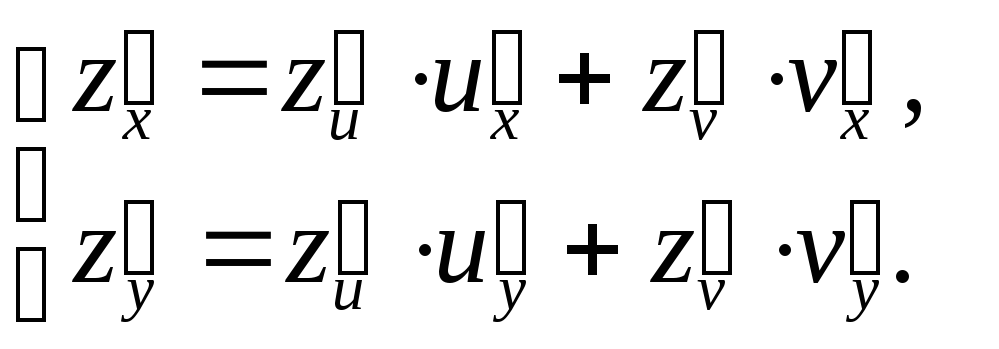(3)

Замечание 1. Формулы (1), (2), (3) легко обобщаются на случай функций трех и более переменных.

Замечание 2. Формулы (1), (2), (3) необходимы в теории для получения других важных результатов. На практике в случае конкретных функций нетрудно исключить зависимость функции от промежуточных переменных. Например, если

а и, токак функцияимеет вид