§11. Экстремумы функции нескольких переменных

Пусть функция определена в некоторой областии пусть– внутренняя точка этой области.

Определение 1. Говорят, что функция имеет в точкелокальный максимум (минимум), если существует такая окрестность точки, в которой выполняется неравенство

().

Если знак “=” достигается только в точке , то максимум (минимум) называется собственным, в противном случае – несобственным. Точки максимума и минимума называются точками экстремума.

Теорема 1. (необходимое условие экстремума). Если функция име-ет экстремум в точкеи обладает в этой точке частными производными перво-го порядка, то эти производные обращаются в ноль в точке.

Доказательство. Пусть для определенности – точка максимума функции. Рассмотрим функцию одной переменнойТогда в некоторой окрестности точки, т.е точка– это точка максимума функции. Кроме того, – дифференцируема в точке , ибо. В силу теоремы Ферма, т.е и. Аналогично доказывается и равенство.

Определение 2. Точки, в которых все частные производные первого поряд-ка функции обращаются в, называются стационарными точками данной функии.

Замечание 1. Если – стационарная точка функии, то касательная плоскость к поверхности, заданной уравнением:, в точкеимеет уравнение, т.е горизонтальна.

Замечание 2. Экстремумы могут быть не только в стационарных точках, но и в точках, в которых хотя бы одна из производных ине существует или имеет бесконечное значение.

Замечание 3. Не во всякой стационарной точке функция имеет экстремум. Например, для функции точка– стационарная:=y, = x обращаются в ноль в начале координат. Но в этой точке функция не имеет ни мак-симума, ни минимума, ибо , а в любой окрестности этой точки функ-ция принимает как положительные, так и отрицательные значения.

Чтобы сформулировать достаточное условие экстремума функции двух пе-ременных введем специальные обозначения. Пусть – стационарная точка функциии пусть в ее окрестности существуют непрерывные част-ные производные второго порядка. Обозначим,,,(напомним, что ) и

.

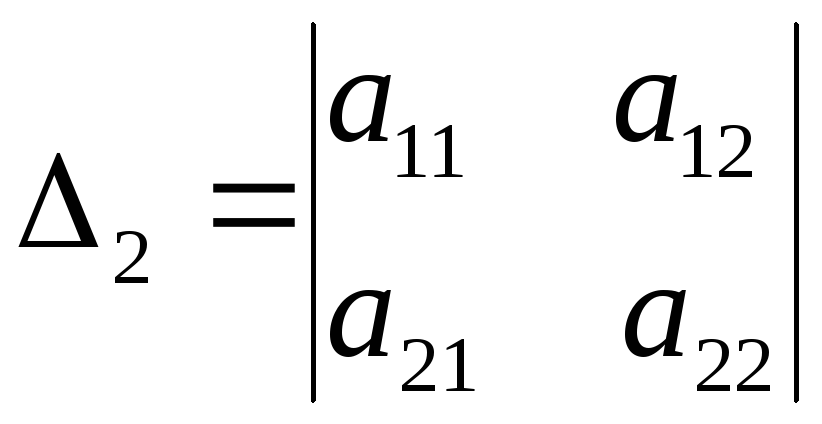Теорема 2 (достаточное условие экстремума).

1. Функция z=имеет в своей стационарной точкеэкстремум, если, причем– точка минимума, если, и точка максимума, если.

2. Если , то в точкенет экстремума.

3. Случай требует дополнительного исследования.

Рассмотрим теперь случай функции переменных. Путь точка– стационарная точка, т.еПредположим, что в некоторой окрестности этой точки существуют непрерывные частные производные второго порядка. Обозначим

i, j = 1,2,…,n.

Из этих чисел составим матрицу . Определители, составленные из эле-ментов первыхстрок истолбцов, называются главными минорами данной матрицы:

,

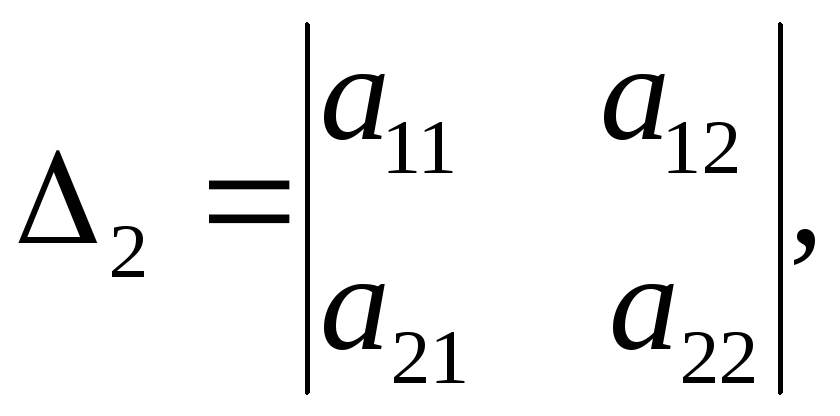
Теорема 3. 1) Если все главные миноры положительны, то функция имеет в точке локальный минимум. 2) Если знаки миноров чередуются, причем, то– точка локального максимума.

Пример 1. Исследовать на экстремум функцию

.

Решение. Находим частные производные первого порядка: Находим стационарные точки:

Имеем две стационарные точки и. Чтобы исследовать эти точ-ки, вычисляем производные второго порядка:

Составим из этих производных определитель:

.

В точке :следовательно, в точкенет экстре-мума. В точке:следовательно, в точкефункция имеет экстремум; так както этот экстремум – минимум.

Пример 2. Исследовать на экстремум функцию трех переменных

.

Решение. и

Имеем две стационарные точки: и. Далее:

, ,

, ,.

Вычислим эти производные в точке и составим матрицу

.

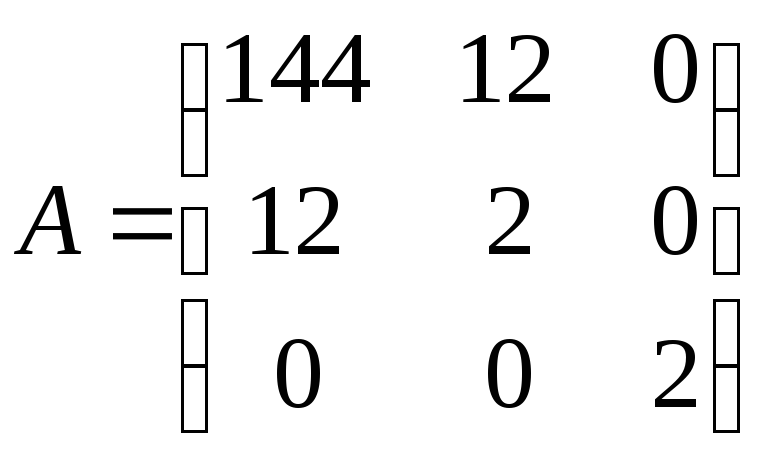Найдем главные миноры:

Все главные миноры положительные, значит – точка минимума.

В точке матрица вторых проиводных имеет вид

Минор Это означает, что требуется дополнительное исследование. В точ-кефункция равнаВ то же время, при изменении аргументов функции вдоль прямой

функция имеет вид и в сколь угодно малой окрестности точкипринимает как положительные, так и отрицательные значения. Следо-вательно, в этой точке нет экстремума.