§2. Определение функции нескольких переменных

Определение 1. Если каждой m-мерной точке М(х₁, х₂, … х^m) из некоторого множества D R^m поставлено в соответствие по некоторому правилу одно определенное число u, то говорят, что на D задана функция n переменных и пишут: u = F(x₁, x₂,… x_n) или u = u(M).

Примером такой функции может служить среднее арифметическое коорди- нат точки:

.

Можно дать и другое, более прозрачное, определение функции, например, двух переменных.

Определение 2. Пусть x, y, z – переменные величины. Если каждой паре возможных значений независимых переменных х и у поставлено в соответствие по некоторому правилу одно определенное значение переменной z, то говорят, что z – есть функция х и у, и пишут: z = f(x, y), или z = z(x, y), или z = z (M), где М(х, у).

Основной способ задания ФНП – аналитический в явной или неявной форме:

z = x² + y² , x² + y² + z² = R².

Если функция f(M) задана на множестве D R^m, то это множество называют областью определения функции. Например, для функции имеем:

,

а для функции –

График функции двух переменных z = z(x,y) – это поверхность в пространстве R³ : .

§3. Предел функции нескольких переменных. Непрерывность

Для простоты впредь будем рессматривать функции двух переменных.

Определение 1. Число b называют пределом функции z = z(x,y) в точке М₀(х₀,у₀) и пишут

,

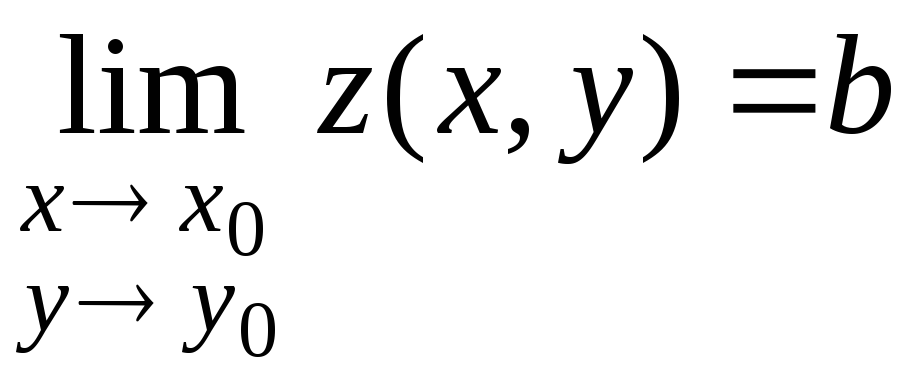если для любой последовательности точек сходящейся к точке

M₀ (т.е x_n→x₀, y_n→y₀), имеем

.

Все свойства и теоремы о пределах функций одной переменной остаются справедливы и для ФНП. Правда, для ФНП нет понятия односторонних пределов.

Примеры.

1. Так как sinα ~ α, при α → 0, то

.

2. Рассмотрим функцию и последовательность точек

, сходящаяся к началу координат O(0,0). Соответствующая последовательность значений функции

имеет предел, зависящий от последовательности {M_n}. Следовательно, предел функции в начале координат не существует.

Определение 2. Функция z(x,y) называется непрерывной в точке , если

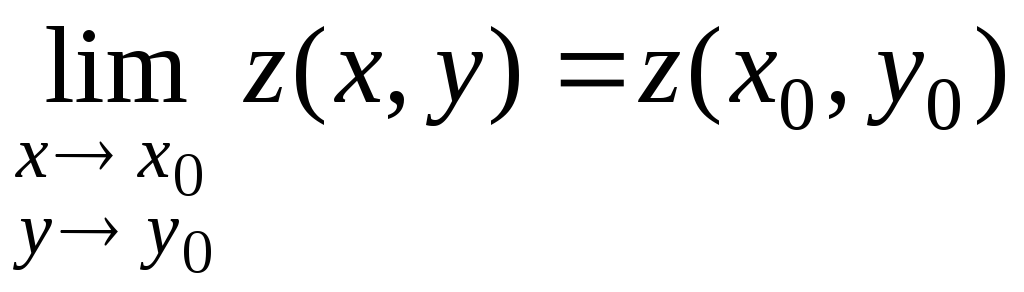. (1)

Определение 3. Функция z (x,y) называется непрерывной в области G, если она непрерывна в каждой точке .

Свойства ФНП, непрерывной в ограниченной замкнутой области, аналогичны свойствам функции одной переменной, непрерывной на замкнутом промежутке. Приведем некоторые из них.

1) Функция z(х,y), непрерывная в ограниченной замкнутой области , ограничена в , и достигает наибольшего и наименьшего значений.

2) Если z(х,y) , то в некоторой окрестности точки функция сохраняет знак.

Замечание. Соотношению (1), определяющему непрерывность функции в точке, можно придать другую форму.

Будем называть полным приращением функции z(x,y) в точке

разность:

Если обозначить то нетрудно получить утверждение:

непрерывность функции z(x,y) в точке равносильна равенству

.

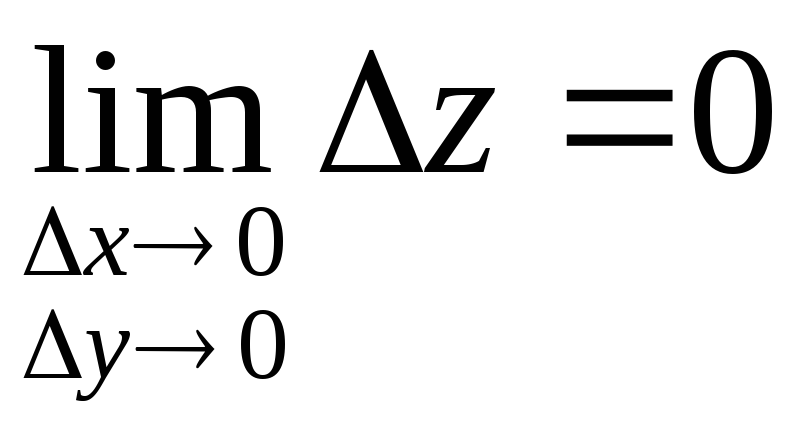Лекция 18

§4. Частные производные

Пусть функция z(x,y) определена в некоторой окрестности точки . Придадим переменной x приращение , т.е. перейдем от точки к точке . При этом таково, что лежит в указанной окрестности точки . Тогда соответствующее приращения функции

называется частным приращением функции z(x,y) в точке .

Аналогично определяется частное приращение функции по переменной :

.

Определение. Предел вида называется частной производной функции z(x,y) в точке по переменной и обозначается одним из символов:

.

Аналогично определяется и частная производная по переменной :

.

Из определения следует, что частная производная функции двух переменных по переменной представляет собой обычную производную функции одной переменной f(x) = z(x,y₀). Поэтому частные производные вычисляются по формулам и правилам вычисления производных функций одной переменной.

Примеры.

1.

2.

Замечание. График функции z = z(x,y) есть некоторая поверхность в пространстве. Тогда

–

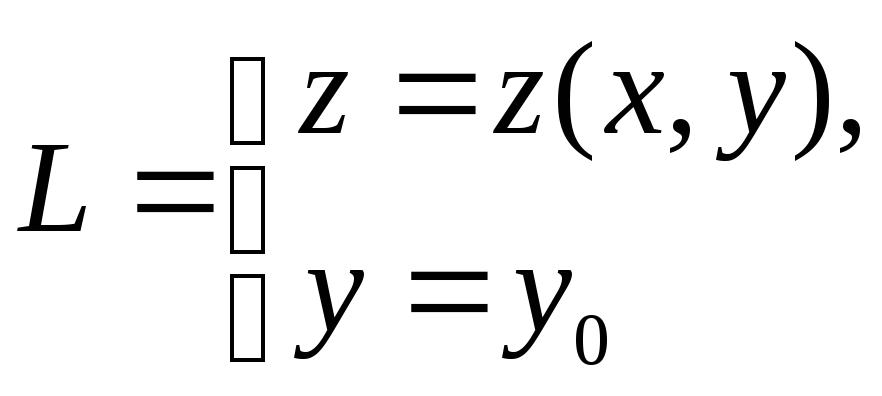это некоторая кривая (плоская) в пространстве и есть не что иное, как угловой коэффициент касательной к L в точке ( ).