II Приближённые вычисления

Как уже отмечалось, остаточный член формулы Тейлора – это погрешность приближённого равенства , где – многочлен Тейлора для функции . С оценкой этой погрешности (см. §3) связаны следующие задачи.

А) Какова погрешность приближённой формулы если изменяется в промежутке

В силу пункта II, §4, для п=3имеем

.

Искомая погрешность не превосходит 0,0025.

В) Какой многочлен Тейлора для функции обеспечит в промежутке ^{погрешность}

В силу пункта III, §4, имеем

Учитывая, что , для нахождения порядка многочлена , получаем ^{неравенство т.е.} .

Подбором получим:

Итак, п=3и искомый многочлен имеет вид:

С) В каком промежутке изменения приближённая формулаобеспечит погрешность

Как и в задаче А) имеем неравенство или .

Итак, искомый промежуток изменения х – это .

Iiі Исследование функций

Теорема (третье достаточное условие экстремума и точки перегиба). Пусть функция имеет в точкепроизводные доп-го порядка включительно, причём Тогда:

1) если – чётное число, то– точка экстремума (точка минимума прии точка максимума при);

2) если – нечётное число, то для графика функции точкаявляется точкой перегиба.

Доказательство. Из условий теоремы следует, что

Эту формулу легко преобразовать к виду

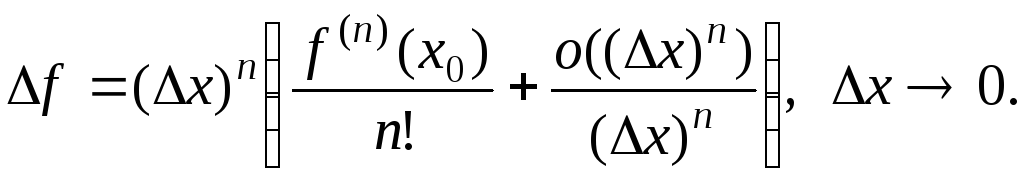
Второе слагаемое в скобках (по смыслу символа ) стремится к нулю при^{, а первое – это некоторое число, отличное от нуля. Поэтому для малых} значений знак скобки совпадает со знаком.

Если число – чётное, тои знакне влияет на знак, т.е.– точка экстремума. При этом, еслито и, значит– точка минимума, а еслито ии– точка максимума.

Если число – нечётное, то знакзависит от знака. Кроме того, в силу условиякасательная к графику функции в точке– горизонтальная. Следовательно, график слева и справа от этой точки находится по разные сторон от касательной, т.е. в этой точке график имеет перегиб.

Пример 3. Для функции точкаявляется стацио-нарной, ибоДалее:

Так как первая, не обратившаяся в ноль производная, чётного порядка, то ноль – точка экстремума, а именно точка минимума, ибо .

106