Сполучення з повтореннями

Задача. Скільки існує різних кидань двох однакових кубиків?

Рішення. Усього при підкиданні одного кубика можливі шість ситуацій – маємо предмети шести різних типів. Підкидають два кубики, отже, з даних шести типів предметів необхідно вибрати два, причому нас не цікавить порядок вибору, і допускається вибір однакових предметів. Таким чином, це задача на сполучення з повторенням. По формулі для обчислення кількості сполучень із повторенням маємо різних кидань двох однакових кубиків.

Біном Ньютона

Задача. Розкрити дужки й привести подібні члени у виразі (3х+2у)⁴, використовуючи формулу бінома Ньютона.

Рішення.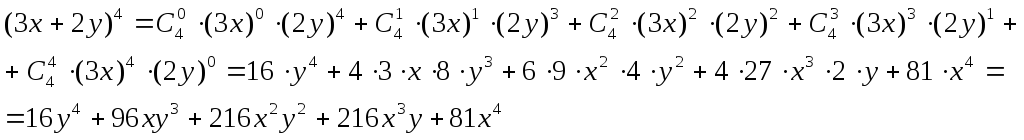

Задача Знайти коефіцієнт при х² у розкладанні (2х+3)⁶.

Рішення. У даній задачі потрібно знайти коефіцієнт тільки при х², тому немає необхідності розкривати все вираження по формулі бінома Ньютона. Досить розглянути тільки один доданок

.

Поліноміальна формула

Задача. Розкрити дужки й привести подібні члени у вираженні (x+y+z)⁴, використовуючи поліноміальну формулу.

Рішення. Ясно, що коефіцієнти при x²yz й xy²z рівні. Тому досить знайти коефіцієнти для таких розбивок n=k₁+k₂+…k_m, що k_1k_2…_k_m, а потім переставляти показники всіма можливими способами. Для нашого приклада маємо:

4=4+0+0; 4=3+1+0; 4=2+2+0; 4=2+1+1;

Р(4,0,0) =1; Р(3,1,0) =4; Р(2,2,0) =6; Р(2,1,1) =12.

(x+y+z)⁴=

=x⁴+y⁴+z⁴+4x³y+4x³z+4y³x+4y³z+4z³x+4z³y+6x²y²+6x²z²+6y²z²+12x²yz+12xy²z+12xyz²

Задачі для самостійної роботи студента

Задача 1.Скільки тризначних чисел можна скласти з цифр 1,2,3,4,5?

Задача 2.Скільки п'ятизначних чисел можна скласти , якщо кожну можна використовувати не більш одного разів?

Задача 3.В класі вивчають 10 предметів. В один день проводяться 6 уроків причому різних. Скількома способами можна скласти розклад на один день?

Задача 4.В кімнаті 6 лампочок. Скільки різних способів освітлення, при яких горить 2 лампочки? Скільки всього способів освітлення кімнати?

Задача 5.Написати програму генерування перестановок множини {1, ..., n} (кожна подальша створюється у результаті 1-кратної транспозиції сусідніх елементів).

Задача 6. Доведіть, C_n⁰+C_n²+C_n⁴+...=?=2^n-1.

Задача 7.Скільки різних слів можна скласти, переставляючи літери слова КОМБІНАТОРИКА?

Задача 8.Скільки різних сигналів можуть дати 5 світлофорів одночасно?

Задача 9.Довести з викладками формулу бінома Ньютона, вживаючи метод математичної індукції.

Задача 10. Вказати найбільше серед чисел .(біном Ньютона)

Задача 11. Знайти n , якщо відомо , що у розкладі (1+x)ⁿ коефіцієнти при x⁵ та x¹² рівні (біном Ньютона)

Задача 12.Написати програму обчислення чисел Фібоначі (та контрольний приклад):

F1 до F1000.

Контрольні питання

1. Дати визначення перестановкам, сполученням та розміщенням. Навести приклади.

2. Сформулювати правило добутку.

3. Сформулювати правило суми.

4. Що називають біномом Ньютона?

5. Що представляють собою з’єднання з повтореннями? Навести приклади.

Лабораторна робота №4

Тема роботи: Комбінаторика. Рекурентні співвідношення. Твірні функції

Мета роботи:Опрацювання практичних навичок у рішенні комбінаторних задач за допомогою рекурентних співвідношень та твірних функцій.