Плоскі графи. Розфарбування графа

10. Знайдіть хроматичні числа для:

• цілком незв'язного графа з n вершинами;

• повного графа з n вершинами;

• двочасткового графа, частки якого мають n й m вершин;

• дерева з n вершинами.

11. Для графів, зображених на малюнку, знайдіть хроматичні числа і яке-небудь правильне розфарбування.

12. Скількома способами можна розфарбувати повний позначений граф на 6 вершинах шістьома кольорами? (Два способи вважаються різними, якщо деяка вершина при одному способі має один колір, а при іншому способі - іншій).

13. Визначте хроматичні числа для графів платонових тіл:

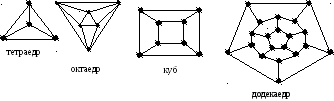
14. Напишіть програму, що по заданій матриці суміжностей і двом вершинам графа обчислює:

(а) кількість шляхів заданої довжини між даними двома вершинами;

(б) загальна кількість шляхів між заданими двома вершинами;

(в) довжину найкоротшого шляху між заданими двома вершинами.

Контрольні питання

1. Що називається циклом? Простим циклом? Ланцюгом? Простим ланцюгом?

2. Що таке правильне розфарбування графа?

3. Який цикл називається ейлеревим?

4. Який цикл називається гамільтоновим?

5. Які алгоритми пошуку мінімальних шляхів в графі вам відомі?

Лабораторна робота №7

Тема роботи: Остов у графі. Мережа. Пошук максимального потоку в мережі.

Мета роботи: Опрацювання практичних навичок у рішенні мережних задач та в находженні остова графа.

Теоретичні відомості

Остов у графі й алгоритм Краскала пошуку в зваженому графі мінімальної ваги. Нехай - граф і- вагова функція, всі графи зв'язні. Остовом графа, є підграф, що є деревом і утримуючий усі вершини даного графа. Вага підграфа - це сума ваг його ребер. Алгоритм Краскала дозволяє знайти остов мінімальної ваги в будь-якому зваженому графі. Його опис по кроках.

Крок 1. Знайдемо в даному графі ребро мінімальної ваги (якщо таких декілька, фіксуємо кожне). Позначимо його через ; крім того, фіксуємо підграф у даному графі, у складі якого є кінці ребраі саме це ребро. Позначимо цей підграф через.

Крок 2. Фіксуємо в даному вихідному графі друге ребро - позначимо його через, - вага якого мінімальна щодо ваг усіх ребер, що не належать. Підграф, що складається з ребер,і їхніх кінців позначимо через.

Крок 3. Фіксуємо в графі ребро - позначимо його через, - має мінімальну вагу серед усіх ребер графа, що не належать, і не є частиною циклу з ребрами з. Підграф, що складається з ребер,,і їхніх кінців, визначимо через.

Крок 4. Фіксуємо в графі ребро - позначимо його через, - має мінімальну вагу серед тих ребер графа, що не належатьі не утворюють циклу з ребрами з. Підграф, що складається з ребер,,,і їхніх кінців визначимо через.

Загальний крок - крок № k. Фіксуємо в графі ребро – позначимо його через, - має мінімальну вага серед ребер, що не входять ві не є частиною циклу з ребрами з. Підграф, що складається з ребер,,,...,, позначимо через.

Пошук максимального потоку у мережі

Транспортною мережею називається зв'язний орієнтований граф, усім дугам якого приписані позитивні числа с_ij, названі пропускними здібностями, при цьому дві вершини графа виділені і називаються полюсами (вхідним – S і вихідним – T), з яких у полюс S не входить жодна дуга, а з полюса T жодна дуга не виходить.

Потоком у даній мережі називається усяка система позитивних чисел a_ij (a_ij – потік у дузі, що виходить з вершини i і входить у вершину j), що задовольняє двом умовам:

1. i,j a_ijc_ij;

2. i (S,T) _ja_ji=_ka_ik,

де перша сума складається з потоків у всіх дугах вхідних у вершину i, а друга – з потоків у всіх дугах з цієї вершини вихідних. У такий спосіб рівність 2 зображуює умови збереження речовини у всіх вершинах мережі, крім полюсів. Величиною потоку називають_ia_Si.

У силу збереження речовини маємо _ia_Si=_jaj. Це рівняння можна істотно узагальнити, саме розіб'ємо множину усіх вершин мережі на дві підмножини N_S і N_T.

Будемо вважати, що S належить N_S, а T належить N_T. Речовина, що перетинає границю між N_S і N_T дорівнює сумі потоків у дугах, що перетинають цю границю з N_S у N_T, мінус сума потоків у дугах, що перетинають ту ж границю в зворотному напрямку. З умов збереження речовини випливає, що для будь-якого фіксованого потоку в даній мережі і для будь-якої розбивки мережі на N_S і N_T, зазначена величина є постійною і рівною величині даного потоку.

Розрізом даної мережі є усяка розбивка множини її вершин на множини N_S і N_T. Пропускною здатністю розрізу назвемо суму пропускних здібностей усіх дуг, що ведуть з N_S у N_T. Зі сказаного випливає, що всякий потік у даній мережі може мати величину не переважаючих пропускних здібностей кожного з розрізів даної мережі. Мінімальним розрізом назвемо розріз, пропускна здатність якого мінімальна серед усіх розрізів даної мережі. Очевидно, що величина максимального потоку в мережі не перевершує пропускної здатності і її мінімального розрізу. Звідси випливає, що якщо деякий потік у даній мережі має величину рівну пропускної здатності якого-небудь розрізу даної мережі, те 1) цей розріз мінімальний, 2) цей потік максимальний.