Теоретичні відомості.

Рекурентне співвідношення має порядок k, якщо воно дозволяє виразити f(n+k) через f(n), f(n+1),…,f(n+k-1).

Наприклад, f(n+2)=f(n)f(n+1)-3f²(n+1)+1 - рекурентне співвідношення другого порядку, а f(n+3)=6f(n)f(n+3)+f(n+1) - рекурентне співвідношення третього порядку.

Якщо задано рекурентне співвідношення k-го порядку, то йому задовольняє нескінченно багато послідовностей. Справа в тому, що перші k елементів послідовності можна задати зовсім довільно - між ними немає ніяких співвідношень. Але якщо перші k елементів задані, те всі інші елементи визначаються однозначно. Користуючись рекурентним співвідношенням і початковими членами, можна один за іншим виписувати члени послідовності. Але в багатьох випадках потрібно довідатися тільки один певний член послідовності, а інші не потрібні. У цих випадках зручніше мати явну формулу для n-го члена послідовності.

Рішенням рекурентного співвідношення є послідовність, якщо при підстановці цієї послідовності співвідношення тотожно виконується.

Наприклад, послідовність 2,4,8,…,2n,… є одним з рішень рекурентного співвідношення f(n+2)=3f(n+1)-2f(n).

Загальний член цієї послідовності має вигляд f(n)=2ⁿ. Виходить, f(n+2)=2ⁿ⁺², f(n+1)=2ⁿ⁺¹. Але при кожному n має місце тотожність 2ⁿ⁺²= 3·2ⁿ⁺¹-2·2ⁿ. Тому 2ⁿ є рішенням зазначеного співвідношення.

Рішення рекурентного співвідношення k-го порядку називається загальним, якщо воно залежить від k довільних постійних C₁, C₂,…, C_k і шляхом підбора цих постійних можна одержати будь-яке рішення даного співвідношення.

Лінійні рекурентні співвідношення з постійними коефіцієнтами

Для рішення рекурентних співвідношень загальних правил немає. Однак існує клас співвідношень, що розв'язується однаковим методом. Це - рекурентні співвідношення виду

f(n+k) = a₁f(n+k-1)+ a₂f(n+k-2)+ … + a_kf(n),

де а₁, а₂,…, а_k - деякі числа. Такі співвідношення називають лінійними рекурентними співвідношеннями з постійними коефіцієнтами.

Розглянемо, як вирішуються такі співвідношення при k=2, тобто вивчимо співвідношення виду f(n+2)= a₁f(n+1)+ a₂f(n).

Рішення цих співвідношень засновано на наступних двох твердженнях:

1. Якщо f₁(n) і f₂(n) є рішеннями рекурентного співвідношення, то при будь-яких числах A і B послідовність f(n)=A f₁(n)+B f₂(n) також є рішенням цього співвідношення.

2. Якщо r₁ є коренем квадратного рівняння r²= a₁ r₊ a₂, то послідовність 1, r₁, r₁²,… r₁^n-1 є рішенням рекурентного співвідношення f(n+2)= a₁f(n+1)+ a₂f(n).

Із тверджень 1 та 2 випливає наступне правило рішення лінійних рекурентних співвідношень другого порядку з постійними коефіцієнтами.

3. Нехай дане рекурентне співвідношення f(n+2)= a₁f(n+1)+ a₂f(n). Складемо квадратне рівняння r²= a₁ r₊ a₂, яке називається характеристичним для даного співвідношення. Якщо це рівняння має два різних корені r₁ , r₂, то загальне рішення співвідношення має вигляд .

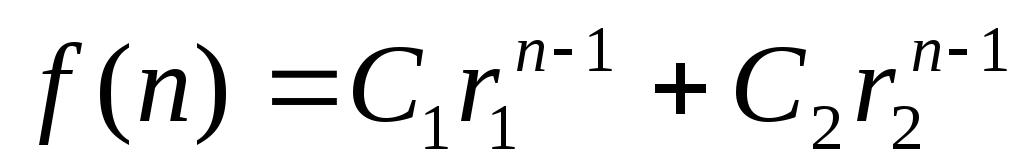Якщо це рівняння має два рівних корені r₁ , r₂, то загальне рішення співвідношення має вигляд .

Метод рекурентних співвідношень дозволяє вирішувати багато комбінаторних задач. Але в ряді випадків рекурентні співвідношення досить важко скласти. Найчастіше ці труднощі вдається обійти, використавши твірні функції.