Задачі по темі Твірні функції:

Задача 1. Знайти твірну функцію послідовності

Рішення: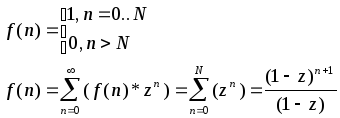

Задача 2. Знайти твірну функцію послідовності

Рішення:

Задача 3. Знайти твірну функцію послідовності

Рішення:

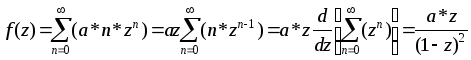
Задача 4.Знайти твірну функцію для f1(n) через твірну функцію для f(n), якщо

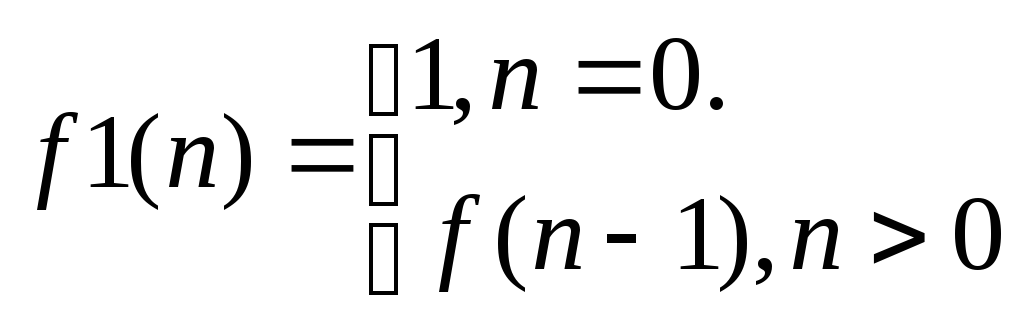
Рішення:

Задача 5. Знайти експоненціальну твірну послідовностіf1(n) ,виражену через , якщо.

Рішення:

Задача 6. Знайти експоненціальну твірну послідовності,виражену через, якщо.

Рішення:

Задача 7.Вирахувати числа Стірлінга 2 роду (S (10, r))

Рішення: таблиця чисел Стірлінга 2 роду (N=8):

S (n,r)	r = 1	r = 2	r = 3	r = 4	r = 5	r = 6	r = 7	r = 8
S (1,r)	1
S (2,r)	1	1
S (3,r)	1	3	1
S (4,r)	1	7	6	1
S (5,r)	1	15	25	10	1
S (6,r)	1	31	90	65	15	1
S (7,r)	1	63	301	350	140	25	1
S (8,r)	1	127	966	1701	1050	266	28	1

Задачі для самостійної роботи студентів

Задача 1. Знайти послідовність {an}, що задовольняє рекурентному співвідношенню

2·an+2 + 5·an+1 + 3·an = 0· и начальним умовам a1=1, a2=2.

Задача 2.Знайти послідовність {an}, що задовольняє рекурентному співвідношенню

4·an+2 + 9·an+1 + 5·an = 0· и начальним умовам a1=1, a2=4.

Задача 3.Знайти послідовність {an}, що задовольняє рекурентному співвідношенню

an+2 - 3·an+1 + 2·an = 0· и начальним умовам a1=3, a2=7.

Задача 4. Знайти послідовність {an}, що задовольняє рекурентному співвідношенню

4·an+2 + 7·an+1 + 3·an = 0· и начальним умовам a1=2, a2=1.

Задача 5. Програти алгоритм генерування всіх розбивок числа для n=4.

Задача 6. Знайти твірну функцію

Задача 7. Знайти твірну функцію для f1(n) через твірну функцію для f(n), якщо

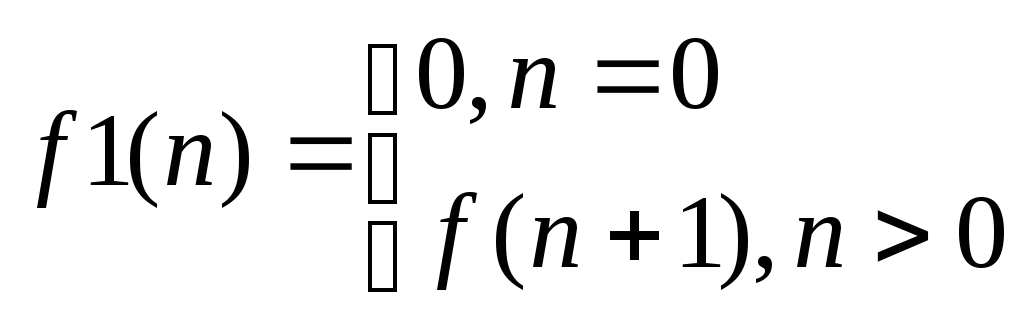
Задача 8. Знайти твірну функцію для f1(n) через твірну функцію для f(n), якщо

Задача 9. Знайти експоненціальну твірну послідовностіf1(n) , виражену через , якщо

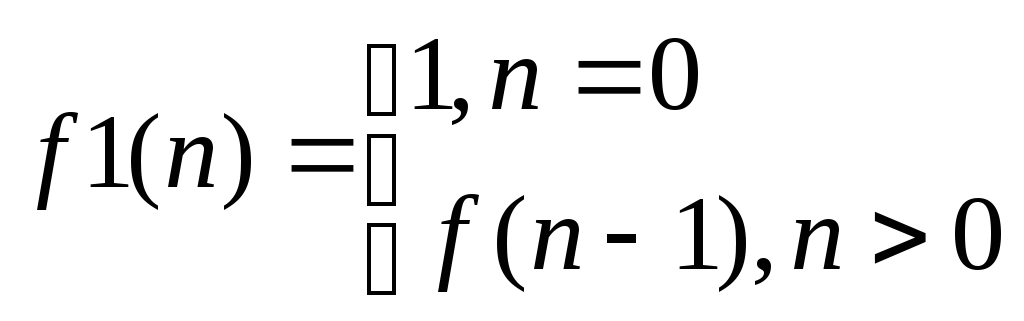
Контрольні питання

1. Що таке твірна функція? Її призначення.

2. Що називають рекурентним співвідношенням k-го порядку?

3. Що визначають числа Стірлінга 1-го та 2-го роду?

Лабораторна робота №5.

Тема роботи:Графи. Способи зберігання інформації о графах в ЕОМ

Мета роботи: Вивчення основних визначень й прикладів графів. Опрацювання практичних навичок у рішенні задач на графах.

Теоретичні відомості

Граф G(V,E) - сукупність двох множин: вершин V, ребер E, між якими визначене відношення інцидентності. Кожне ребро e з E інцидентно рівно двом вершинам v', v'', що воно з'єднує. При цьому вершина v' і ребро e називаються інцидентними один одному, а вершини v' і v'' називаються суміжними. Якщо |V(G)|=n, |E(G)|=m, то граф G є (n,m) граф, де n - порядок графа, m - розмір графа.

• Ребро (v',v'') може бути орієнтованим і мати початок (v') і кінець (v'') (дуга в орграфі).

• Ребро (v,v) називається петлею (кінцеві вершини збігаються).

• Граф, що містить орієнтовані ребра (дуги), називається орграфом.

• Граф, що не містить орієнтовані ребра (дуги), називається неографом.

• Ребра, інцидентні одній парі вершин, називаються кратними.

• Граф із кратними ребрами називається мультиграфом.

• Граф, що містить петлі (і кратні ребра), називається псевдографом.

• Порожній граф - множина ребер порожня (число вершин може бути довільним).

• Повний граф - граф без петель і кратних ребер, кожна пара вершин з'єднана ребром. Позначення для повного графа з n вершинами - K_n.

• Граф називається двочастковим, якщо існує така розбивка множини його вершин на дві частин, що кінці кожного ребра належать різним частинам (часткам).

• Якщо будь-які дві вершини двочасткового графа, що входять у різні частки, суміжні, то граф називається повним двочастковим.

• Локальний ступінь вершини - число інцидентних їй ребер. У неографі сума ступенів усіх вершин дорівнює подвоєному числу ребер (лема про рукостискання). Петля дає внесок, рівний 2 у ступінь вершини.

• Наслідок 1 з леми про рукостискання. Довільний граф має парне число вершин непарного ступеня.

• Наслідок 2 з леми про рукостискання. Число ребер у повному графі n(n-1)/2.

• Графи рівні, якщо множина і вершин і інцидентних їм ребер збігаються.

• Графи, що відрізняються тільки нумерацією вершин і ребер, називаються ізоморфними.

• Граф називається регулярним (однорідним), якщо ступені всіх його вершин рівні.

• Вершина і є досяжною для вершини j, якщо існує маршрут з і в j.

• Граф є зв’язаним, якщо всі його вершини є досяжними для кожної вершини.

• Компонента зв’язності - це максимально зв’язаний підграф.