Алгоритми пошуку мінімальних шляхів у графі

Алгоритм Дейкстри — знаходить найкоротший шлях від одної вершини графа до всіх інших вершин.

Найпростіша реалізація алгоритму Дейкстри використовує масив відстаней та масив позначок. На початку алгоритму відстані заповнюються великим позитивним числом (більшим максимально можливого шляху в графі), а масив позначок заповнюється нулями. Потім відстань для початкової вершини вважається рівною нулю і запускається основний цикл.

На кожному кроці циклу ми шукаємо вершину з мінімальною відстанню і прапором рівним нулю. Потім ми встановлюємо в ній позначку 1 і перевіряємо всі сусідні з нею вершини. Якщо в ній відстань більша, ніж сума відстані до поточної вершини і довжини ребра, то зменшуємо його. Цикл завершується коли позначки всіх вершин стають рівними 1.

Алгоритм Флойда - розв'язує проблему знаходження всіх пар найкоротших шляхів в підвішеному направленому графі.

Ініціалізація:

1. Побудуємо матрицю D⁰ розмірності |V| x |V|, елементи якої визначаються за правилом:

1. d_ii⁰= 0;

2. d_ij⁰= Weight(v_i, v_j), де i<>j, якщо в графі існує ребро (дуга) (v_i, v_j);

3. d_ij⁰= нескінченність , де i<>j, якщо немає ребра (дуги) (v_i, v_j).

2. m:=0.

Основна частина:

1. Побудуємо матрицю D^m+1 по D^m, обчислюючи її елементи наступним чином: d_ij^m+1=min{d_ij^m, d_i(m+1)^m + d_(m+1)j^m}, де i<>j; d_ii^m+1=0 (*). Якщо d_im^m + d_mi^m < 0 для якогось i, то в графі існує цикл (контур) від’ємної довжини, що проходить через вершину v_i; ВИХІД.

2. m:=m+1; якщо m<|V|, то повторюємо крок (1), інакше елементи останньої побудованої матриці D^|V| рівні довжинам найкоротших шляхів між відповідними вершинами; ВИХІД.

КІНЕЦЬ

Якщо потрібно знайти самі шляхи, то перед початком роботи алгоритму побудуємо матрицю P з початковими значеннями елементів p_ij=i. Кожного разу, коли на кроці (1) значення d_ij^m+1 буде зменшуватися відповідно з (*) (тобто коли d_i(m+1)^m + d_(m+1)j^m<d_ij^m), виконуємо присвоювання p_ij:=p_(m+1)j. В кінці роботи алгоритму матриця P буде визначати найкоротші шляхи між усіма парами вершин: значення p_ij буде означати номер передостанній вершини в маршруті між i и j (або p_ij=i, якщо шлях не існує).

Якщо граф - неорієнтований, то всі матриці D^m є симетричними, тому досить обчислювати елементи, котрі розташовані вище (або тільки нижче) головної діагоналі.

Задачі на теорію графів

Задача 1.Знайти всі шляхи з Х4 в Х7 у графі G = (Х, Г) зображеному на рис. 6.7.

Рис. 6.7. – Граф для задачі 1

Рішення

Маршрути, які ведуть з Х4 в Х7:

Х4, Х3, Х2, Х1, Х7

Х4, Х3, Х2, Х1, Х8, Х6, Х7

Х4, Х3, Х2, Х1, Х8, Х7

Х4, Х3, Х6, Х2, Х1, Х7

Х4, Х3, Х6, Х2, Х1, Х8, Х7

Х4, Х3, Х6, Х7

Х4, Х3, Х6, Х8, Х1, Х7

Х4, Х3, Х6, Х8, Х7

Задача 2.В графі знайти довжину найкоротшого шляху з Х4 в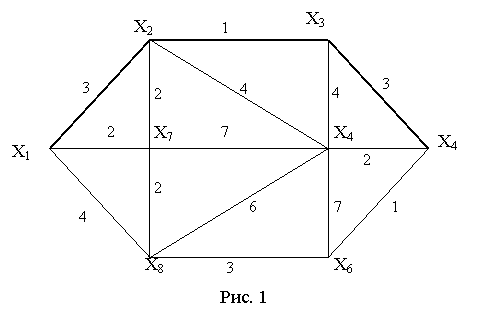 Х1Відповідь - найкоротший маршрут: (Х1, Х2, Х3, Х4) або (Х4, Х3, Х2, Х1).

Задача 3. Пошук контурів фіксованої довжини

Алгоритм використовує матрицю суміжності A і матриці A^k-1 і Ak, якщо довжина контурів, що відшукуються, дорівнює k. Виберемо деяке i, таке, що a_ii^(k)=1. Це означає, що вершина v_i належить контуру довжини k. Тоді вершина v_j належить тому ж контуру, якщо виконуються наступні три умови:

- a_jj^(k)=1; - a_ij=1, тобто існує шлях довжини 1 з v_i у v_j; - a_ji^(k-1)=1, тобто існує шлях довжини k-1 з v_j у v_i.

Алгоритм заснований на послідовній перевірці умов до виявлення усіх вершин контуру. Реалізуйте наведений алгоритм відшукання контурів фіксованої довжини.

Задача 4. Задача економії пам'яті.

Припустимо, що необхідно написати програму для обчислення функції j (х1, x2, ..., xn). Обчислення цієї функції розбито на ряд блоків, у кожного з блоків є вхідні і вихідні змінні (рис.6.8). Так, наприклад, у блоку 2 вхідні змінні a і b, вихідна - с, у блоку 3 вхідна змінна a, вихідна - d.

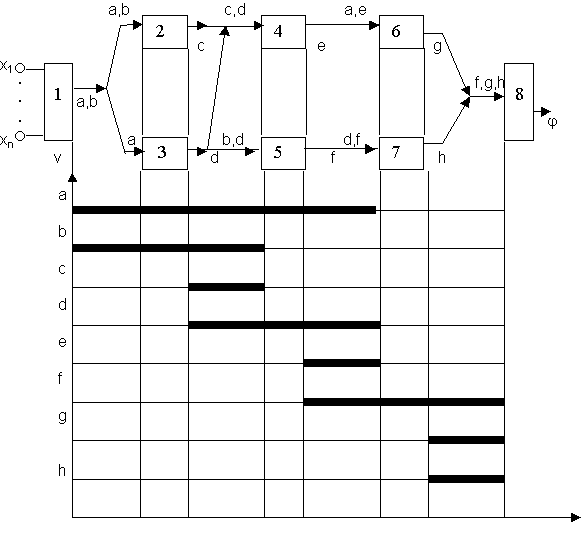
Рис. 6.8 - Процес обчислення функції j (х1, x2, ..., xn)

Верхню частину рисунку можна назвати блок-схемою інформації. Нижня частина цього рисунка є «система координат», де по вертикальній осі відкладені введені в блок-схемі змінні, а по горизонтальній «час їх життя» при обчисленні значення функції j.

Припустимо, що значення змінної займає одну комірку пам'яті. Завдання полягає в тому, щоб визначити найменше число комірок пам'яті, необхідне для зберігання зазначених блок - схемою змінних. Вирішити це завдання можна таким чином. На множині змінних V = {a, b, ..., g, h} введемо структуру графа: дві змінних з'єднаємо ребром, якщо часи їхнього життя перетинаються. Отриманий граф будемо називати графом несумісності змінних (див. мал. нижче). Значення змінних не можуть займати одну клітинку пам'яті тоді і тільки тоді, коли змінні з'єднані ребром у графі несумісності. Отже, завдання економії пам'яті зводиться до знаходження оптимальної розмальовки вершин графа несумісності. У нашому випадку досить чотирьох елементів пам'яті (рис.6.9).

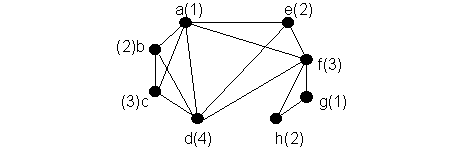
Рис. 6.9 – Рішення задачі економії пам’яті