
Modul_II
.pdf
Полагая в формуле Тейлора |
, получаем формулу Макларена: |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
20.2Разложение по формуле Макларена функций
1)Разложение функции
Т.к. |
и |
|
|
, получаем |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
При х =1получим формулу, позволяющую найти приближенное значение числа е:
2) Разложение функции |
. |
– мы получили исходное выражение. Т.е. результаты повторяются с циклом 4. Поэтому
Представление |
в виде многочлена с нечетными степенями было ожидаемо |
|||||
из-за нечетности функции |
, а формула Макларена дала необходимые |
|||||
коэффициенты! |
|
|
|
|
|
|
Вычислим |
. Чтобы применить формулу Макларена нужно от угла в |
|||||
размерной величине (градусы) |
перейти к безразмерной величине (радианы) по |
|||||
известной формуле |
|
|
|
|
|
: |
|
|
|
||||
51

3) Разложение функции |
. |
– мы опять получили исходное выражение, и результаты снова повторяются с циклом 4. Поэтому
Очевидно, представление |
в виде многочлена с четными степенями тоже |
ожидаемо из-за четности функции |
. |
20.1Связь между функциями
Великий Леонард Эйлер первым в вел в математике новое число названную в дальнейшем мнимой единицей. Он обнаружил, что степени этого
числа обладают циклом 4: |
, |
, |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
Кроме того, члены разложения по степеням для |
и |
являются, с |
|
|||||||||||||||||||||||||||||
точностью до знака, четными и нечетными частями разложения функции |
. |
||||||||||||||||||||||||||||||||
Поэтому он разложил функцию |
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. В результате мы получили знаменитую формулу Эйлера
которая устанавливает связь между тригонометрическими и показательными функциями.
Несложные алгебраические преобразования позволяют тригонометрические функции выразить через показательные функции:
– практически совпадающие с выражениями для введенных в аналитической геометрии гиперболических функций:
52
Примеры для самостоятельной работы по разделу «Производная».
1)Пользуясь определением производной, найти производные следующих функций:
|
|
|
|
a) |
|
|
|
|
|
|
|
; |
|
|
б) |
|
|
|
|
|
|
|
|
|
|
|||||
2) |
Продифференцировать указанные функции : |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
а) |
|
|
|
|
|
|
|
|
|
; |
|
б) |
|
|
|
|
; в) |
; |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
3) |
г) |
|
|
|
|
|
|
|
|
|
|
; |
|
д) |
; |
е) |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
Найти производные второго порядка от указанных функций : |
||||||||||||||||||||||||||||||
|
|
а) |
|
|
|
|
|
|
, |
|
|
; б) |
; |
в) |
. |
|
|
|
|
|
||||||||||
4) |
Составить уравнения касательной и нормали к указанным линиям |
|||||||||||||||||||||||||||||
либо в указанной точке |
, |
либо при указанном значении параметра . |
||||||||||||||||||||||||||||
5) |
|
|
|
а) |
|
|
|
, |
|
; |
|
|
б) |
, |
|
. |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Найти указанные пределы с помощью правила Лопиталя : |
||||||||||||||||||||||||||||||
|
а) |
|
|
; |
|
б) |
|
|
|
|
; |
в) |
|
|
|
; |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
г) |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Лекция 21. Исследование поведения функций.
21.1Возрастание и убывание функций.
Т. Для того, чтобы дифференцируемая на отрезке функция была возрастающей (убывающей) необходимо и достаточно, чтобы на
этом |
отрезке |
ее производная была неотрицательной |
|
|
||||||
(неположительной |
) |
|
|
|
|
|
|
|||
Доказательство. |
Докажем сначала необходимость. |
Пусть функция |
|
|
||||||
для |
. Тогда |
|
при |
и |
при |
|||||
|
, поэтому |
|
|
при любом знаке |
, |
|
|
|
||
|
|
|
, |
|
|
|||||
Так как функция дифференцируема, то |
|
|
|
|
|
|||||
|
|
|
|
|
||||||
|
. Что и требовалось доказать. |
|
|
|
|
|
||||
Докажем достаточность. |
|
Пусть |
|
. Возьмем |
любые |
|||||
числа |
|
|
и применим к отрезку |
|
теорему Лагранжа, |
|||||
|
|
|
|
|
|
|
|
|
53 |
|

тогда |
|
, здесь |
|
. Т.к. |
и |
, то |
|
при |
, а это |
значит что |
|
– что и требовалось доказать. |
|
|
Аналогично доказывается теорема и для убывающей функции.
21.2Экстремум функций.
df 1. Функция f(x) в точке x1 имеет минимум (minimum), если в любой, сколь угодно малой -окрестности точки x1, значение функции f(x)
больше ее значения в точке x1
|
. |
Иначе говоря, функция f(x) имеет min в точке х1, если для любого знака |
|
сколь угодно малого приращения аргумента |
. |
df 2. Функция f(x) в точке x2 имеет максимум (maximum), если в любой, сколь угодно малой -окрестности точки x2, значение функции f(x) меньше
ее значения в точке x2
|
. |
Иначе говоря, функция f(x) имеет max в точке х2, если для любого знака |
|
сколь угодно малого приращения аргумента |
. |
Так, функция изображенная на рисунке 1 имеет min в точках х2 |
и х4 а max в |
точках х1, х3, х7. |
|
Замечание 1.Фукция, определенная на |
|
отрезке может достигать экстремумов только |
|
внутри этого отрезка. |
|
Замечание 2. Не надо думать, что |
|
максимум и минимум функции являются ее |
|
наибольшим и наименьшим значением на |
|
всем рассматриваемом отрезке: в точке |
|
максимума функция имеет наибольшее |
|
значение только в малой окрестности xmax, а в точке минимума – наименьшее |
|
значение только в малой окрестности xmin . Как видно на этом рисунке минимум
функции в точке х4 расположен выше максимума |
в точке х1. |
Максимумы и минимумы функции называются экстремумами |
функции. |
Как видно из рис.1, экстремумы |
бываю гладкими и острыми. При этом в |
||||
точках гладкого |
экстремума ( |
функция |
имеет горизонтальную |
||
касательную, |
а в |
точках острого |
экстремума |
– либо вертикальную |
|
касательную, |
либо не имеет касательную (касательная слева от точки |
не |
|||
совпадает с касательной справа).
Такие точки называются критическими точками. Таким образом, все точки экстремума являются критическими точками. Однако не все критические точки являются точками экстремума. Так, точки являются критическими, однако экстремума в них нет! Если сравнить поведение кривой вблизи этих точек и вблизи точек экстремума, то отличие сразу бросается в глаза: вблизи этих точек
54
характер монотонности кривой не меняется, а вблизи точек экстремума характер монотонности меняется. Причем, если кривая из монотонно возрастающей становится монотонно убывающей, то критическая точка является точкой максимума, а если кривая из монотонно убывающей становится монотонно возрастающей – то точкой минимума.
Докажем теперь, что в точках гладкого экстремума касательная к кривой
горизонтальна, и |
согласно геометрического |
смысла производной |
|
|
||||||||||||||
|
|
. Доказательство проведем для максимума. Пусть функция |
в точке а |
|||||||||||||||
имеет максимум. Согласно определения, |
в любой, сколь |
угодно малой |
||||||||||||||||
окрестности точки, |
|
|
|
для любого знака |
, |
|
|
|
||||||||||
|
|
|
. Тогда знак отношения |
|
|
|
определяется знаком |
, поэтому |
||||||||||
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
и |
|
|
|
|
. Т.к. по условию функция |
||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
дифференцируема |
в точке а, |
то из |
свойств пределов |
|
|
|
|
|
||||||||||
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
, |
|
|
. Это равносильно |
|
, что и |
||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
требовалось доказать. Случай минимума доказывается аналогично. |
|
|
||||||||||||||||
Т.к. вертикальная |
прямая |
перпендикулярна горизонтальной |
прямой, то |
|||||||||||||||
|
|
|
, |
|
|
. |
Поэтому в точках острого экстремума |
|
|
, |
||||||||
|
|
|
|
|
|
|||||||||||||
либо . |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Поэтому, для |
нахождения |
точек |
экстремума функции |
сначала находят |
||||||||||||||
критические точки функции, а затем с помощью достаточного признака экстремума определяют, какие из критических точек являются точками экстремума.
Т . ( достаточные условия существования экстремума). Пусть
функция непрерывна в некотором интервале, содержащем критическую точку , и дифференцируема во всех точках этого интервала (кроме, быть может, самой точки ). Если при переходе слева направо
через эту точку производная меняет знак с плюса на минус, то при |
|
функция имеет максимум. Если же при переходе через точку |
слева |
направо производная меняет знак с минуса на плюс, то функция имеет в этой точке минимум. Таким образом, если:
a) |
при |
х |
|
при |
х |
||
|
|||
то в точке х1 функция имеет максимум; |
|
|
|
б) |
при |
х |
|
при |
х |
||
|
то в точке х1 функция имеет минимум. При этом надо иметь в виду, что условия
а) или б) должны выполняться для всех значений х, достаточно близких к х1, т. е. во всех точках некоторой достаточно малой окрестности критической точки
х1.
55
Д о к а з а т е л ь с т в о . Предположим |
сначала, |
что производная меняет знак с |
|||
плюса на минус, т. е. что для х, достаточно близких к точке х1, имеем |
|||||
|
|
|
при |
х |
|
|
|
|
при |
х |
|
|
Применяя теорему Лагранжа к разности |
, получим |
|||
|
|
|
|
, |
|
где с – точка, лежащая между х и х1 . |
|
|
|
||
1) |
Пусть |
, тогда |
|
|
|
|
|
, |
, |
, |
поэтому |
|
, |
или |
. |
|
|
2) |
Пусть |
, тогда |
|
|
|
|
|
, |
, |
, |
поэтому |
|
, |
или |
. |
|
|
Значит, в окрестности точки |
|
, и согласно определения, в |
|||
точке |
функция имеет максимум, что и требовалось доказать. Аналогично |
||||
доказывается вторая часть теоремы о достаточных условиях минимума.
21.3Исследование поведения функций с помощью формулы Тейлора.
Пусть в стационарной точке |
|
|
равны нулю все производные, вплоть до |
||||
n-го порядка. Тогда формула Тейлора в малой окрестности точки |
имеет |
||||||
вид |
|
|
. |
|
|
|
|
|
|
|
|
||||
1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
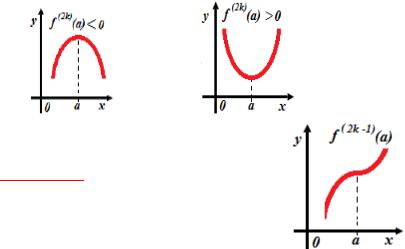
Графиком такой функции является квадратичная парабола. Т.к. |
, то |
||||||
вид параболы определяется знаком производной |
. Очевидно, если |
||||||
, то точка |
является точкой минимума, а если |
, то |
|||||
точкой максимума. |
|
|
|
|
|
|
|
2)
В этом случае графиком функции является кубическая парабола, которая экстремумов не имеет.
21.4Выпуклость и вогнутость кривой. Точки перегиба
56

Рассмотрим на плоскости кривую y = f ( x ), являющуюся графиком однозначной дифференцируемой функции f (x ) .
df1. Мы говорим, что кривая обращена выпуклостью вверх на интервале , если все точки кривой лежат ниже любой ее касательной на этом
интервале.
Мы говорим, что кривая обращена выпуклостью вниз на интервале если все точки кривой лежат выше любой ее касательной на этом интервале. Кривую, обращенную выпуклостью вверх, будем называть выпуклой, а обращенную выпуклостью вниз – вогнутой.
На рисунке показана кривая, выпуклая на интервале ( а , b ) и вогнутая на интервале (b , с).
Направление выпуклости кривой является важной характеристикой ее формы. Настоящий параграф посвящен установлению признаков, по которым можно было бы, исследуя функцию y = f (x ) , судить о направлении выпуклости ее графика на различных интервалах.
Докажем следующую теорему.
T . Если во всех точках интервала ( а , b ) вторая производная функции f ( х )
отрицательна, т. е. |
, то на этом интервале кривая y = |
f (x ) |
выпукла, а если вторая производная функции f ( х ) отрицательна, |
т. е. |
|
, то на этом интервале кривая вогнута. |
|
|
Д о к а з а т е л ь с т в о . |
Возьмем в интервале (а , b ) произвольную точку х = х0 |
|||||||||||
и проведем касательную к кривой в точке |
с абсциссой х = х0. Уравнение |
|||||||||||
касательной к кривой в точке х0 |
имеет вид |
|
|
|
|
. |
||||||
Применим к функции |
формулу Тейлора с точностью до |
|
: |
|||||||||
|
|
|
|
|
|
|
|
|
, |
|
||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
, малой окрестности точки |
|
и |
|||||
|
|
|
|
|
|
|||||||
членом |
можно пренебречь. Поэтому |
|
|
|
|
. |
||||||
|
|
|
|
|||||||||
Т . к . |
, то знак этого выражения |
определяется |
знаком второй |
|||||||||
производной в точке х0: а) при |
и |
|
|
– кривая лежит |
||||||||
выше касательной, т.е. кривая вогнутая; б) |
при |
|
|
и |
|
|||||||
|
– кривая лежит ниже касательной, т.е. кривая вогнутая, что и требовалось |
|||||||||||
доказать. |
|
|
|
|
|
|
|
|
|
|
||
df. Точка, в которой график кривой |
|
меняет |
свою |
кривизну |
||||||||
называется точкой перегиба. |
|
|
|
|
|
|
|
|||||
|
Очевидно, в точке перегиба |
|
, если в |
|
|
|||||||
точке |
функция дифференцируема и второй |
|
|
|||||||||
производной не существует, если непрерывная |
|
|
||||||||||
функция не дифференцируема в этой точке. |
|
|
|
|
|
|||||||
Действительно, пусть в точке |
функция |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
57 |

дифференцируема и |
|
и пусть, например, слева от точки |
кривая выпукла, а справа – вогнута. Это значит, что слева вторая |
||
производная отрицательна и |
, а справа вторая |
|
производная положительна и |
. Т.к. вторая производная в |
|
точке а существует, то |
, |
|
|
, что и требовалось доказать. |
|
Приложение. Кривизна кривой.
Мы выяснили, что знак второй производной на некотором интервале определяет выпуклость или вогнутость графика функции на этом интервале. Однако, одни функции более выпуклы (вогнуты), чем другие. Установим меру изогнутости кривой . Введѐм понятие, которое характеризует это явление. Пусть мы имеем кривую, которая не пересекает сама себя и имеет определѐнную касательную в каждой точке. Проведѐм касательные к кривой в каких-нибудь двух еѐ точках А и В и обозначим через угол, образованный этими касательными, или, точнее – угол поворота касательной при переходе от точки А к точке В (рис. 1). Этот угол называется углом смежности. Угол смежности в некоторой степени даѐт представление о степени изогнутости дуги. У двух дуг, имеющих одинаковую длину, больше изогнута та, у которой угол
рис. 1 |
рис. 2 |
смежности больше (рис. 2,1). |
|
Полной характеристикой изогнутости кривой будет отношение угла смежности к длине соответствующей дуги.
df. Средней кривизной дуги называется отношение соответствующего угла смежности к длине дуги:
Для одной и той же кривой средняя кривизна еѐ различных дуг может быть различной; так, например, для кривой (см. рис. 3) средняя кривизна дуги АВ не равна средней кривизне дуги А1В1 , хотя длины этих дуг равны между собой.
58
Отметим, что вблизи различных точек кривая искривлена по-разному. Для того чтобы охарактеризовать степень искривлѐнности данной линии в непосредственной близости к данной точке А, введѐм понятие кривизны в данной точке.
df. Кривизной |
линии в данной точке А называется предел средней |
кривизны дуги АВ, когда длина этой дуги стремится к нулю:
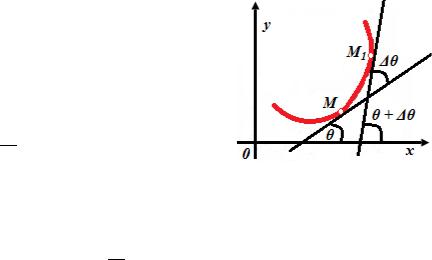
Проведѐм касательные к кривой в точках M и M1 с абсциссами x и x+ x и обозначим через θ и θ + Δθ углы наклона этих касательных. Длину дуги MM1 обозначим через . Как видно из рисунка, угол смежности, соответствующий дуге равен абсолютной величине разности углов θ и θ + Δθ, то есть равен Δθ.
Согласно определению средней кривизны кривой на участке имеем .
Чтобы получить кривизну в точке М, нужно найти предел полученного выражения при условии, что длина дуги стремится к нулю:
.
Так как величины θ и зависят от x, то можно считать, что эта функция задана
параметрически с помощью параметра x. Тогда |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
Согласно |
геометрического |
|
смысла производной |
|
|
|
. Отсюда |
||||||||||||||||||||||||||
, |
|
|
|
|
|
|
|
|
|
|
. |
Для |
нахождения |
|||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||
производной |
|
воспользуемся определением производной |
|
|
|
|
|
|
|
и длину |
||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||
дуги |
|
заменим на длину секущей |
|
|
|
, причем согласно теоремы |
||||||||||||||||||||||||||||
Пифагора |
|
|
|
|
|
|
|
|
|
|
|
. Т.к. |
, |
то |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
и точное равенство получается при |
|
, т.е. |
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
59 |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||

. Тогда формула для вычисления кривизны кривой принимает вид
|
|
|
|
|
|
|
|
(1). |
|
|
|
|
|
|
|
|
|
||
Если кривая задана параметрически: |
, то исходя из соответствующих |
||||||||
формул |
|
и |
|
, получаем |
|
|
(2) |
||
|
|
|
|
||||||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||
Если кривая задана в полярной СК уравнением вида ρ = (φ), то подставляя
это выражение в формулы перехода от полярной СК к ПДСК |
, |
||
получаем уравнение кривой в параметрической форме |
и после |
||
несложных алгебраических преобразований, получаем |
|
||
|
|
. |
(3) |
|
|||
df. Величина R, обратная кривизне К линии в данной точке М, называется радиусом кривизны этой линии в рассматриваемой точке: R = 1/K.
В ПДСК |
|
(4). |
|
Построим в точке М нормаль к кривой, направленную в сторону вогнутости кривой, и отложим на этой нормали отрезок МС, равный радиусу R кривизны кривой в точке М. Точка С называется центром кривизны данной кривой, а круг радиуса R с центром в точке С (проходящий через точку М) называется кругом кривизны данной кривой в точке М.
Из определения круга кривизны следует, что в данной точке кривизна кривой и кривизна круга кривизны равны между собой. Выведем формулы, определяющие координаты центра кривизны.
Пусть кривая задана уравнением |
. Зафиксируем на кривой точку M(x, y) |
и определим координаты a и b |
центра кривизны C(a, b) соответствующего |
этой точке. Для этого напишем уравнение нормали к кривой в точке М:
60
