
Modul_II
.pdf
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|||||||||||
|
|
– что и требовалось доказать. |
|
|
|
|||||||||||||
|
|
П1. Найти производную функции |
|
. |
|
|||||||||||||
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Замечание. Если функция задана неявно |
|
, то переменная у является |
|||||||||||||
зависимой переменной, т.е. функцией |
независимой переменной х. Поэтому |
||||||||||||||
при нахождении , производные от выражений с у, содержащиеся в |
|||||||||||||||
функциональной зависимости |
|
, необходимо пользоваться формулой |
|||||||||||||
производных для сложной функции. |
|
|
|
|
|
|
|
|
|||||||
|
|
|
П 3. Найти производную функции |
. |
|
|
|||||||||
Записывая это выражение в виде |
|
|
|
|
|
получаем функцию |
|||||||||
заданную неявно. Дифференцируем эту функцию по аргументу х: |
|||||||||||||||
|
|
|
|
|
|
, |
|
|
|
|
|
, |
|||
|
|
|
|
|
, |
|
|
|
|
. Для нахождения производной, |
|||||
|
|
|
|
|
|||||||||||
разрешим это уравнение относительно : |
|
|
|
, |
|||||||||||
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
. |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Приложение. Таблица производных
41

–
ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ
|
|
|
|
|
4. |
1. |
|
|
|
|
; |
2. |
|
|
|
|
|
|
|
|
|
|
5. |
3. |
|
|
|
; |
6. |
|
|
;
;
Лекция 18. Производные старших порядков |
|
|
18.1 Производные степенной и показательной функций |
|
|
1) Найдем производную степенной функции |
, |
. |
В этом случае эту функцию можно логарифмировать, в результате чего получим
|
|
|
|
. Тогда |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
. |
||
|
|
|
|
|
|
|||||
Легко показать, что эта формула верна и для |
. |
|
|
|||||||
П 1. Найти производную |
. |
|
|
|
||||||
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
П 2. Найти производную |
. |
|
|
|
||||||
42

2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Найдем производную показательной функции |
|
|
. Логарифмируя это |
||||||||||||||||||
|
|
выражение, получим |
|
|
|
|
. Тогда |
||||||||||||||
|
|
|
|
|
|
, |
|
. |
|
|
|||||||||||
|
|
|
|||||||||||||||||||
Т.к. |
|
|
|
, то |
. |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
П 3. Найти производную |
|
. |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
П 4. Найти производную |
. |
|
|
|||||||||||
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
. |
||
П 5. Найти производную |
. |
|
|
|
|
|||||||||
Чтобы найти производную, прологарифмируем это выражение |
||||||||||||||
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
. |
|||||
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|||||
Таким образом, производная от функции |
равна сумме производных |
|||||||||||||
степенной и показательной функций. |
|
|
|
|||||||||||
18.2Производная обратных тригонометрических функций
1)Производная обратной функции.
|
Пусть функция |
|
|
|
|
|
непрерывна и монотонна на интервале (a,b). |
||||||||||||||||||||
Тогда на этом интервале она имеет обратную функцию |
|
, которая тоже |
|||||||||||||||||||||||||
непрерывная функция. Это значит, что при |
|
приращение функции |
|||||||||||||||||||||||||
|
|
|
при |
приращение обратной функции |
: |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
и |
|
|
|
. Воспользовавшись определением предела, получаем |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
Таким образом |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
2) Производная функции |
. |
|
|
|
|
|
|
|
||||||||||||||||||
Т.к. в своей области определения |
|
функция является монотонно |
|||||||||||||||||||||||||
возрастающей, то на этом отрезке она имеет обратную функцию |
. |
|
|||||||||||||||||||||||||
Воспользовавшись формулой для обратной функции, получаем |
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
43
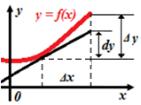
Аналогично показывается, что |
|
|
|
|
|
|
. |
|
|
||||||||
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|||||||||||||
3) |
Производная функции |
|
|
. |
|
|
|
|
|
|
|
|
|||||
Т.к. в своей области определения |
|
функция является монотонно |
|||||||||||||||
возрастающей, то на этом отрезке она имеет обратную функцию |
. |
|
|||||||||||||||
Воспользовавшись формулой для обратной функции, получаем |
|
|
|||||||||||||||
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Аналогично показывается, что |
|
|
|
. |
|
|
|
||||||||||
|
|
|
|
|
|||||||||||||
18.3 |
|
Дифференциал |
|
|
|
|
|
|
|
|
|
|
|
||||
Найдем приращение функции |
: |
|
|
|
|
|
|
|
. |
||||||||
df. Линейная часть приращения функции |
(относительно приращения |
||||||||||||||||
аргумента ) называется дифференциалом функции dy. |
|
|
|||||||||||||||
В нашем примере |
. Для единообразия обозначений, в |
|
|
||||||||||||||
дифференциале приращение аргумента обозначается как dy. Поэтому для нашего
примера |
|
. Коэффициент перед |
|
|
– |
является производной х2, т.е. |
||||||||||||||||||||||
|
|
|
. Таким образом для нашего примера |
|
|
и приращение функции |
||||||||||||||||||||||
|
|
|
|
|
|
, или |
|
|
). Оказывается, что выражения |
|||||||||||||||||||
и |
|
справедливы для любой функции. |
||||||||||||||||||||||||||
|
|
|
П1. Найти дифференциал функции |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|||||||
|
|
|
Очевидно |
|
|
|
|
, или |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
– формула приближенных вычислений. |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
П2. Вычислить |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Полагая х = 98, получаем функцию |
|
. Т.к. |
|
|
|
|
|
, то |
||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
. Беря в качестве а ближайший квадрат 100, получим |
||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
Дифференциал имеет простой геометрический смысл. Для этого запишем |
|||||||||||||||||||||||||
уравнение касательной |
|
|
|
|
|
|
|
|
|
виде |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. Записав |
||||||||||||||
дифференциал в исходном виде |
|
видим, что правые |
||||||||||||||||||||||||||
части выражений для дифференциала и приращения касательной совпадает, поэтому дифференциал является
приращением касательной к графику функции.
18.4Производная функции, заданной параметрически
44
Найдем производную функции, заданной параметрически |
|
|
. Для этого |
||||||||
найдем дифференциалы х и у: |
и |
. Тогда |
|
|
|
|
|
|
|||
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
П3. Найти производную функции |
. |
|||||||
|
|
|
|
|
|
|
|
|
18.5Производные и дифференциалы различных порядков
|
|
В общем случае, производная функции |
|
является функцией аргумента х и |
||||||||||||
|
|
мы можем ее дифференцировать. |
|
|
|
|
|
|
|
|
||||||
|
|
df. Производная первой производной называется производной второго |
||||||||||||||
|
|
порядка или второй производной. |
. |
|
|
|
|
|
||||||||
|
|
Аналогично, производная второй производной называется производной |
||||||||||||||
|
|
третьего порядка или третьей производной |
. |
|
|
|||||||||||
|
|
И вообще, производной n-го порядка от функции f(x) называется |
|
|||||||||||||
|
|
производная от производной (n–1)-го порядка и обозначается |
или |
|||||||||||||
|
|
П4. Найти производную четвертого порядка функции |
|
|
|
. |
||||||||||
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
и, наконец, |
|
|
|
|
||||||
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
П4. Найдем вторую производную функции, заданной параметрически |
. |
|||||||||||||||
Согласно определения |
, а |
|
|
. Поэтому |
|
|
|
|
||||||||
|
|
|
|
|
||||||||||||
|
|
|
|
|
, |
|
|
|
|
. |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
В общем случае, дифференциал функции |
|
является функцией |
||||||||||||
|
|
аргумента х, причем от х может зависеть только |
а приращение |
|
||||||||||||
|
|
аргумента |
от значения х не зависит. Найдем дифференциал этой функции. |
|||||||||||||
|
|
df. Дифференциал от дифференциала функции называется |
|
|||||||||||||
|
|
дифференциалом второго порядка или вторым дифференциалом |
: |
|||||||||||||
Найдем выражение второго дифференциала: |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. Очевидно |
|
|
|
|
– другое обозначение второй |
|||||||
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
45 |
производной введенное Лейбницем ( читается «де два у по де х в квадрате»).
Очевидно, дифференциалом n-го порядка от функции f(x) называется
дифференциал от дифференциала (n–1)-го порядка |
, |
|||
причем |
и |
|
. |
|
|
|
|||
Лекция 19. Основные теоремы дифференциального исчисления
19.1 |
Теорема Коши |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Т. Если функции |
и |
непрерывны на отрезке [a,b] и |
|
|
|
||||||||||||||
дифференцируемы на интервале (a,b), причем |
|
на этом интервале, |
|||||||||||||||||
то существует такая точка |
|
|
, что |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Доказательство. |
Составим вспомогательную функцию |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
) |
|
|
|
– здесь число |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Очевидно, функция |
непрерывна на отрезке [a,b] и |
|
|
|
|||||||||||||||
дифференцируема на интервале (a,b). Это значит, что |
|
|
– иначе |
||||||||||||||||
нарушается условие непрерывности и |
|
|
|
|
|
|
|
. |
|||||||||||
Очевидно |
|
|
|
|
. Тогда |
|
|
|
|
|
|
|
|
||||||
1) |
|
, |
|
для |
, для |
|
|
|
, |
|
|||||||||
2) |
|
|
|
|
|
|
|
. |
|
|
|
|
, что внутри интервала |
||||||
|
|
|
|
|
|
|
|
|
|||||||||||
|
. Тогда из непрерывности функции |
||||||||||||||||||
(a,b) существуют точки, в которых функция |
|
принимает наибольшее |
|
||||||||||||||||
значение M и наименьшее значение m. Пусть в точке |
|
|
функция |
|
|||||||||||||||
принимает наибольшее значение M. Очевидно, из-за граничных значений |
|
||||||||||||||||||
( |
|
), M |
0. Тогда в некоторой окрестности точки х = с |
|
|
||||||||||||||
|
<0, независимо от знака х. Поэтому |
|
→ −0 |
|
|
|
а |
||||||||||||
|
|
|
|
|
и из дифференцируемости функции |
|
|
|
|||||||||||
|
, |
|
|
||||||||||||||||
|
|
, что и требовалось доказать. |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|||||||||||||
19.2 |
Теорема Лагранжа |
|
|
|
|
|
|
|
|
||||||||||
Т. Если функция |
|
непрерывны на отрезке [a,b] и дифференцируема на |
|||||||||||||||||
интервале (a,b), то существует такая точка |
|
, что |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
46 |

Доказательство. Взяв функция |
. Тогда |
||||
условия теоремы Лагранжа для функции |
и |
||||
свойства функции |
на отрезке [a,b] |
полностью |
|||
совпадают с условиями теоремы Коши, поэтому |
|||||
|
|
|
, |
|
, что |
|
|
|
|||
и требовалось доказать.
Терема Лагранжа имеет простой геометрический смысл, для этого проанализируем
выражение |
|
|
|
|
|
. Как видно из рисунка, |
||
|
|
|
||||||
из |
|
, что |
|
|
|
|
, где –угол наклона секущей к оси Ох. Т.к. |
|
|
|
|
|
|||||
|
сек –угловой коэффициент секущей, а |
– угловой коэффициент |
||||||
касательной. Тогда |
|
|
|
|
, что является условием |
|||
|
|
|
||||||
параллельности касательной и секущей. Это позволяет дать теореме Лагранжа геометрическую формулировку: Если функция непрерывны на отрезке
[a,b] и дифференцируема на интервале (a,b), то существует такая точка , в которой касательная параллельна секущей, проходящей через
точки |
и |
. |
|
|
|
||
|
19.3 |
Теорема Роля |
|
|
|
||
Т. |
Если функция |
непрерывны на отрезке [a,b] |
|
||||
, дифференцируема на интервале (a,b) и на концах |
|
||||||
отрезка принимает равные значения |
|
, |
|
||||
то |
существует по |
крайней мере |
одна |
точка |
|
||
|
, в которой производная обращается в |
|
|||||
нуль |
|
|
|
|
|
|
|
Доказательство. Т.к. условия теоремы Роля |
|
||||||
|
|
|
|||||
полностью совпадают с условиями теоремы |
|
||||||
Лагранжа, |
то |
, в которой |
|
. Следовательно |
|||
|
|
. Т.к. |
, то |
, |
. |
|
|
|
Терема Роля имеет простой геометрический смысл. Условие |
|
|||||
|
,значит в точке х = с касательная параллельна оси Ох. Тогда |
||||||
геометрическая формулировка теоремы Роля: Если функция |
непрерывны |
||||||
на отрезке [a,b] , дифференцируема на |
интервале (a,b) и на концах отрезка |
||||||
принимает равные значения |
, то существует по крайней мере |
||||||
одна точка |
, в которой касательная параллельна оси Ох. |
|
|
|
|||
19.4 Правило Лопиталя |
|
|
|
|
|
|
|
Правило Лопиталя позволяет раскрывать неопределенности |
|
|
или |
|
|
||
|
|
||||||
|
|
|
|
|
47 |
||
Т. Пусть функции |
и |
|
|
непрерывны и дифференцируемы в |
|||||||||
окрестности точки |
и |
|
|
|
|
|
|
|
|
, предел |
|
|
|
|
|
|
|
|
|||||||||
существует, тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Доказательство. |
|
Докажем теорему для случая |
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
Т.к. условия теоремы полностью соответствуют условиям теоремы Коши, |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
применим теорему Коши для отрезка [a,х] : |
|
|
|
|
|
|
|
|
|
|
|
где с (а,х). Т.к. |
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, то |
|
|
|
|
|
|
|
|
|
|
. Найдем предел этого выражения |
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. Очевидно, что при х а и с, чтобы оставаться в интервале |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
(a,х) тоже а, поэтому |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, что и |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
требовалось доказать. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
Случай |
|
|
|
|
|
|
|
доказывается аналогично. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
Замечание. Если после применения правила Лопиталя опять будет |
|
|
или |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
, его нужно применить еще раз. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
П 1. Вычислить |
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
П 2. Вычислить |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. Это значит, что при |
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
функция |
|
|
|
|
|
|
|
растет медленней, чем функция |
|
|
|
и ее график лежит ниже |
||||||||||||||||||||||||||||||||||||||||||||||||
прямой |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
Неопределенность |
|
|
|
|
|
раскрывается с помощью тождественного |
|
|||||||||||||||||||||||||||||||||||||||||||||||||
преобразования, приводящего ее к неопределенности |
|
|
|
|
или |
|
. |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
П 3. Вычислить |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
||
|
|
|
|
|
|
|
|
|||||||||||||||
П |
4. Вычислить |
|||||||||||||||||||||
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
48 |
|||||||||||||||||||||
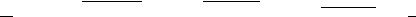
Неопределенности |
, |
и |
возникают при нахождении пределов |
||
и раскрываются с помощью тождественного преобразования |
|||||
: |
|
|
, приводящего их к |
||
неопределенности |
. |
|
|
|
|
П 5. Вычислить |
. |
|
|
|
|
|
|
|
|
|
|
. Воспользовавшись
таблицей эквивалентных б.м., получаем |
|
. |
Лекция 20. Исследование поведения функций
20.1Формула Тейлора
Предположим, что функция |
имеет все производные до (n+1)-го |
||||
порядка |
включительно |
в некотором |
промежутке, содержащем точку |
. |
|
Найдем многочлен |
степени не выше n, значение которого в точке х = |
||||
а равняется значению функции f (x ) |
в этой точке, а значения его производных |
||||
до п - г о |
порядка в |
точке |
равняются |
значениям соответствующих |
|
производных от функции f (x ) в этой точке |
|
|
|||
|
|
|
|
(1) |
|
Естественно ожидать, что в окрестности точки |
такой многочлен мало |
|
|||
отличается от функции f ( х ) . |
|
|
|
||
Будем искать этот многочлен в форме многочлена по степеням |
|
||||
с неопределенными коэффициентами |
|
|
|
||
|
|
|
|
(2) |
|
Неопределенные коэффициенты |
|
определим так, чтобы |
|
||
удовлетворялись условия (1). |
|
|
|
||
Предварительно найдем производные от |
: |
|
|||
|
|
|
|
( 3 ) |
|
Введя понятие n факториал |
|
и вычислив значения |
|
||
многочлена и его производных в точке |
, получим выражение (1) в виде: |
|
|||
|
|
|
|
|
49 |
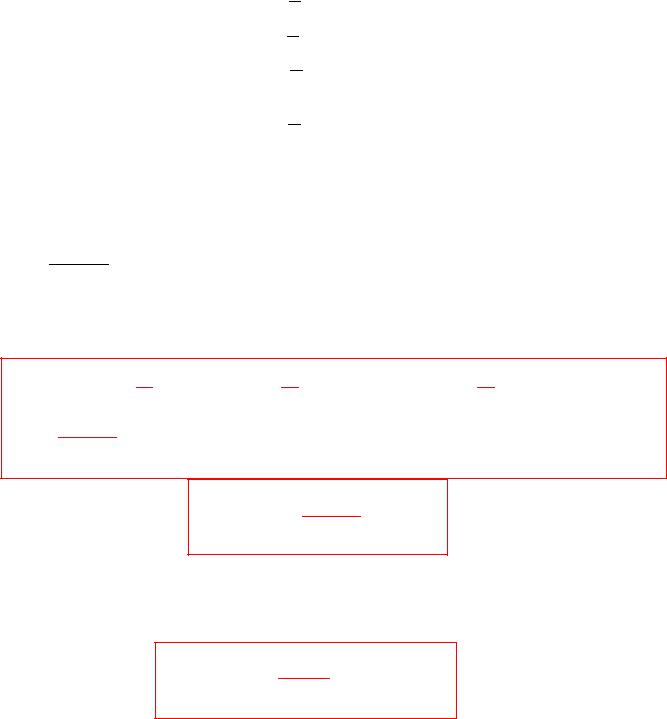
откуда находим коэффициенты :
(4 )
Подставляя найденные значения |
|
, в формулу (2), получим |
||||
искомый многочлен: |
|
|
|
|
||
|
|
|
|
|
|
|
|
Очевидно, в малой окрестности точки |
разность |
будет |
б.м. |
и еѐ называют остаточным членом, поэтому |
|
|
Это выражение называется формулой Тейлора.
Отбрасывая последний член, получаем формулу приближенных вычислений
Если вспомнить, что – приращение функции, и
– n-ый
дифференциал, то приращение функции можно записать в виде
50
