
Скобцовы Моделирование и тестирование
.pdfнеисправность α меняет значения компонент x0 |
,x1 |
на противоположное, |
||||||||
|
|
|
|
|
|
i |
i |
|
|
|
так как |
она |
входит |
списки |
Xi0,X i1 , |
|
получаем |
значения |
|||
0 |
D′ |
D |
|
1 |
|
|
|
~ |
=1. |
Аналогично |
xi |
= 0,xi |
= 0,xi |
= 0,xi =1, которые являются кодом xif |
|||||||
неисправность |
β , |
при |
~ |
|
~ |
= E |
представляется |
|||
которой xi =1 и |
xif |
|||||||||
x0 |
=1 {β }, xD′ = 0{β }, xD = 0{}, x1 = 0{}. |
В |
табл.5.5 |
приведены |
||||||
i |
|
i |
|
i |
i |
|
|
|
|
|
всевозможные комбинации значений xi и xif (в исправном и неисправном ДУ) и их представления в указанной нотации. Теоретико-множественные
операции над входными списками для получения выходных списков
Fi0,FiD′ ,FiD ,Fi1 выводятся из функций fi0,fiD′ ,fiD ,fi1 .
Поскольку это "обычные" булевы функции, то для этих операций
можно использовать известные методы, например, изложенные в [72,73].
Как правило, указанные методы ориентированы на вывод теоретико-
множественных операций для определенных входных наборов двоичных значений данной булевой функции.
Рассмотрим распространение входных списков неисправностей в пятизначном алфавите Е5 на примере вентиля f=ab. Eгo поведение в
алфавите Е5 описывается согласно табл.3.5 следующими компонентами:
f 0 = a0b0 aD′bD aDbD′ , |
f D′ = a D′b1 a1bD′ a D′bD′ |
f D = a Db1 a1bD aDbD , |
f 1 = a1b1. |
Пусть на входах вентиля имеются следующие значения сигналов и списки неисправностей:
a0 = 0, A0 = {a0 , aE , aH , au }; a D′ = 0, AD′ = {aE , au };
a D = 0, AD = {aH , au }; a1 = 1, A1 = {a0};
181
b0 = 1, B0 = {b }; |
|
|
|
|
|
|
|
|
|
|
|
|||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
bD′ = 0, B D′ = {b |
E |
,b }; |
|
|
|
|
|
|||||||
|
|
|
|
u |
|
|
|
|
|
|
||||
bD = 0, BD = {b |
H |
,b }; |
|
|
|
|
|
|||||||
|
|
|
|
u |
|
|
|
|
|
|
||||
b1 = 0, B1 = {b ,b |
E |
,b |
H |
,b }. |
|
|
|
|
||||||
|
1 |
|
|
|
|
|
u |
|
|
|
|
|||
Результаты |
|
показывают, |
что в |
исправном ДУ |
~ |
при |
||||||||
|
f = 0 , а |
|||||||||||||
неисправности b1 |
|
|
|
|
~ |
|
|
|
||||||
имеет место |
f f = E . |
Аналогично при неисправностях |
||||||||||||
~ |
|
|
|
|
~ |
= u . |
Таким образом, |
неисправности a0 ,aE ,aH ,au |
|
|||||
bH − f |
= H ,bu − f |
на |
||||||||||||
выходе |
вентиля |
|
не |
проявляются, |
а неисправности |
b1,bE ,bH ,bu |
||||||||
распространяются на его выход. Если во множество моделируемых неисправностей входят const0 и const1 на выходе вентиля, то мы должны добавить неисправность f1 в списки ( f0 не проверяется). В результате получим F 0 = {b1,f1}, F D′
Основным преимуществом предлагаемого подхода является то, что при разработке моделей цифровых микросхем (правил распространения входных списков неисправностей) не нужно строить новые модели, а
можно использовать универсальные модели для многозначных алфавитов,
предложенные в разделе 3. Поскольку разработаны формальные методы построения моделей, вывод их может быть автоматизирован. Данные модели по сложности не превосходят предложенные в работах [72,73].
5.4 Конкурентный метод моделирования
Этот метод является наиболее общим методом моделирования цифровых схем с неисправностями. Он, как и предыдущий, является одношаговым, то есть для данного входного набора выявляются сразу все проверяемые неисправности. Он позволяет обрабатывать различные типы моделей схем, неисправностей, задержек и сигналов. Метод основан на
182

том, что в процессе моделирования значения сигналов на большинстве линий неисправных схем совпадают со значениями исправной схемы.
Конкурентный метод явно моделирует исправную схему (все ее логические элементы) и для каждой неисправности обрабатывает только те элементы, значения сигналов на которых отличаются от соответствующих значений в исправной схеме. Такие расхождения для каждого элемента собираются в специальный список. В отличие от дедуктивного метода список неисправностей здесь ассоциируется не с линией схемы, а с логическим элементом. При этом список включает не только те неисправности, которые вызывают неправильное значение сигнала на выходе элемента, но и такие, при которых значения сигналов отличны от исправного устройства и на входах элемента. Такой список называют суперсписком неисправностей, так как он обычно существенно шире соответствующего списка дедуктивного метода моделирования.
a=0 |
|
|
|
& |
испр. |
||
b=1 |
|||
|
|||
|
с=1 |
||
|
|
|
a=0 |
|
|
|
& |
3 |
||
b=0 |
|||
|
с=1 |
||
a=0 |
|
|
|
|
|
||
& |
5 |
||
|
|||
b=0 |
|||
|
|||
|
с=1 |
||
a=1 |
|
||
|
|
||
|
|
||
& |
111 |
||
|
|||
b=1 |
|||
|
|
||
|
с=0 |
||
|
|
||
|
|
|
Рис.5.12 Суперсписок вентиля
Вконкурентном методе все неисправности обрабатываются наравне
сисправными устройствами, то есть для неисправности включенной в
183

суперсписок, выполняется моделирование данного элемента явно. Каждый элемент суперсписка включает в себя номер неисправности и значения сигналов на входах и выходах этого элемента при данной неисправности.
Например, на рис.5.12 представлен в графическом виде суперсписок
неисправностей для вентиля c = a b .
Здесь вверху представлен логический элемент со значениями сигналов в исправной схеме. Во втором сверху элементе показано, что при неисправности номер 3 имеют место значения сигналов a=0, b=0, c=1.
Соответственно третий элемент списка показывает, что для неисправности номер 5 a=0, b=0, c=1. Заметим, что одинаковые значения сигналов при неисправностях номер 3 и 5 допускаются. Аналогично для последнего элемента списка имеем a=1, b=1, c=0. Отметим, что только последняя неисправность номер 111 попала бы в список дедуктивного моделирования, связанного с линией c. Заметим, что элементы в суперсписке сортируются по номерам неисправностей для более
эффективной обработки и хранения в связанных списках либо в
последовательных массивах. Так как суперсписок шире списка,
используемого в дедуктивном методе, то затраты памяти выше при конкурентном методе. В дедуктивном методе явно (непосредственно)
моделируются только те элементы, которые исправны. В конкурентном методе явно моделируются те элементы, значения входов или выходов которых отличны от значений исправных схем. В параллельном методе элементы в исправных и неисправных схемах моделируются явно даже в тех случаях, если значения сигналов у них совпадают.
В качестве примера рассмотрим моделирование фрагмента схемы,
представленного на рис.5.13. На нем представлены в графическом виде суперсписки вентилей схемы для входного набора a=0, b=0, d=0, f=0.
Здесь с вентилем с ассоциируется список с константными неисправностями a1, b1, и с0, при которых значения на входах или выходе
184

элемента отличны от исправной схемы. Заметим, что только при неисправности с0 значение выхода элемента с отлично от исправного.
Поэтому эта неисправность распространяется далее по схеме (она включается в суперсписки вентилей e и g).
a=0 |
|
|
|
|
d=0 |
|
|
|
|
|
|
|
|
|
||
& |
|
c=1 |
1 |
|
e=1 |
|
|
|
& |
|
g=0 |
|||||
b=0 |
|
|
|
|
|
|
f =1 |
|
||||||||
|
|
a1 |
|
|
|
|
|
c0 |
|
|
|
c0 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
1 |
|
|
|
0 |
|
|
|
0 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
& |
1 |
1 |
0 |
& |
1 |
||||||||||
|
|
|
|
|
|
|||||||||||
0 |
|
|
0 |
|
0 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
b1 |
|
|
|
a1 |
|
e0 |
|||||||
0 |
|
|
|
1 |
|
|
|
0 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|||||||||
|
|
1 |
|
|
|
|
|
|
|
|
||||||
|
& |
1 |
1 |
& |
1 |
|||||||||||
|
|
|
|
|
|
|||||||||||
1 |
|
1 |
0 |
|||||||||||||
|
|
|
c0 |
|
|
|
e0 |
|
|
|
f 1 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
0 |
|
|
|
1 |
|
|
|
1 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
& |
0 |
1 |
0 |
& |
0 |
||||||||||
|
|
|
|
|
|
|||||||||||
0 |
|
|
0 |
|
1 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
g0 |
|||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
& |
0 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
0 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис.5.13 Пример суперсписков фрагмента схемы
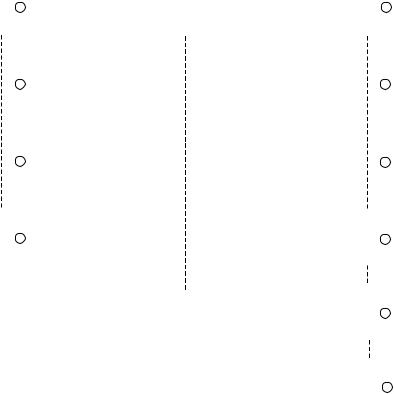
Далее рассмотрим изменение суперсписков, которое происходит вследствие изменения входного набора a : 0 → 1, e : 0 → 1. В результате имеем следующие суперсписки, показанные на рис.5.14.
Видно, что в исправной схеме значение выхода вентиля с не изменяется. При неисправности b1 вентиль с моделируется явно и его выход изменяется с 1 на 0. Заметим, что это событие распространяется далее и попадает в суперсписок, связанный с вентилем g. Очевидно, что неисправность a0 надо добавить в суперсписок с (поскольку при ней значения сигналов отличаются от значений исправной схемы). При неисправности a1 значение сигналов на всех линиях вентиля с совпадает с
185
исправным устройством. Поэтому a1 исключается из суперсписка с.
Аналогично обрабатываются суперсписки для вентилей e и g.
a=1 |
|
|
|
|
|
d=0 |
|
|
|
|
|
|
e=1 |
|
|
|
|
|
|||
& |
|
c=1 |
|
1 |
|
& |
|
g=0 |
|
||||||||||||
b=0 |
|
|
|
|
|
|
|
|
|
|
f=1 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
a0 |
0 |
|
|
|
|
0 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
& |
|
1 |
b1 |
& |
b1 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
0 |
|
|
|
0 |
|
1 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
1 |
|
|
|
0 |
|
1 |
|
||||||||||||
1 |
|
|
0 |
|
|
|
0 |
|
|
|
|
|
|||||||||
|
|
|
b1 |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
& |
|
1 |
c0 |
& |
c |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||
1 |
|
|
|
|
0 |
|
|
|
1 |
|
|
|
|
0 |
|
||||||
|
|
0 |
|
|
|
0 |
|
|
|
|
1 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1 |
|
|
1 |
|
|
|
0 |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
& |
|
c0 |
1 |
d1 |
& |
e0 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
0 |
|
|
|
1 |
|
1 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
0 |
|
|
|
1 |
|
1 |
|
||||||||||||
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
f0 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
1 |
e0 |
& |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
1 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
g1 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
& |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
Рис.5.14 Изменение суперсписков |
|
|
|||||||||||||||
Из этого примера видно, что основными процедурами в конкурентном методе является внесение влияний неисправностей, сужение и расширение суперсписков, обработка последователей элемента. Перед началом моделирования проводится инициализация, в процессе которой все неисправности схемы вносятся в соответствующие суперсписки. Это делается локально - для каждого элемента в его суперсписок включаются неисправности, при которых входы и выходы элемента имеют значения сигналов, отличные от значений исправной схемы. Далее в процессе моделирования влияние этих неисправностей распространяется по схеме.
Как мы видели на примере, элемент в суперсписке может стать идентичным элементу в исправном устройстве, когда значения их сигналов
186
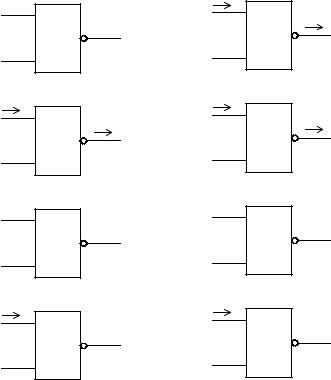
на всех входах и выходах совпадают.
исключен из суперсписка, который совпадение сигналов у исправных и произойти по двум причинам:
Тогда этот элемент должен быть при этом сужается. При этом неисправных элементов может
−изменение сигналов неисправного элемента;
−изменение сигналов исправного элемента.
В первом случае для всех неисправных элементов, которые были
промоделированы, должно быть выполнено сравнение с исправными элементами и в случае совпадения соответствующий элемент исключается из списка. Эта ситуация представлена на рисунке 5.15 а).
|
0 |
& |
|
0 |
1 |
& |
|
|
|
|
|
||||
|
|
|
1 |
|
|
1 |
0 |
|
1 |
|
|
|
1 |
|
|
1 |
0 |
i1 |
|
1 |
0 |
i1 |
|
& |
|
& |
|
||||
|
|
0 |
1 |
|
|
0 |
1 |
|
1 |
|
|
|
1 |
|
|
|
1 |
i2 |
|
|
1 |
i2 |
|
|
& |
|
|
& |
|
||
|
|
0 |
|
|
0 |
||
|
|
|
|
|
|
||
|
1 |
|
|
|
1 |
|
|
1 |
0 |
i3 |
|
1 |
0 |
i3 |
|
& |
1 |
& |
1 |
||||
|
|
|
|
|
|
||
|
0 |
|
|
|
0 |
|
|
|
|
а) |
|
|
|
б) |
|
|
Рис.5.15 Изменение суперсписков |
|
|||||
Во втором случае для всех элементов суперсписка неисправностей должно быть выполнено сравнение с неисправным элементом. Эта
187

ситуация представлена на рисунке 5.15 б).
Очевидно, рассматриваемые процедуры требуют затрат на поиск элементов и просмотр списка, включение и исключение элементов из него.
Аналогично, при какой-либо неисправности в процессе моделирования значения сигналов элемента могут стать отличными от значений сигналов исправного устройства. Тогда в суперсписок должен быть включен соответствующий элемент, что ведет к расширению списка.
Неисправности, при которых значения выходов отличаются от выходов исправных элементов, включаются в суперсписки элементов-
последователей. Если изменились значения элемента в исправной схеме, то кандидатами на включение в список являются неисправности этого
элемента. Эта ситуация представлена на рисунке 5.16.
|
|
0 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
& |
|
1 |
|
|
|
|
|
|
& |
|
1 |
|
||||
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
||||
|
|
|
|
|
|
l1 |
|
|
|
|
|
|
|
|
|
l1 |
|||
|
0 |
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
& |
1 |
0 |
|
|
|
|
& |
1 |
|
||||||||
|
|
1 |
|
|
|
|
u |
0 |
|
||||||||||
|
|
|
|
|
|
l2 |
|
|
|
|
|
|
|
|
l3 |
||||
|
0 |
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
& |
1 |
0 |
|
|
|
|
& |
1 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
1 |
|
|
|
|
|
0 |
|
||||||||||
|
|
|
|
|
|
l3 |
|
|
|
|
|
|
|
|
|
l2 |
|||
|
|
1 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
& |
0 |
|
|
|
|
|
& |
1 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
1 |
|
|
|
1 |
0 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
l4 |
|
|
|
l2 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
0 |
1 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
& |
|
1 |
0 |
|
|
|
|
|
|
& |
|
1 0 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
1 |
|
|
|
|
1 |
0 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис.5.16 Изменение суперсписков
Так как в конкурентном методе моделирование элемента при каждой неисправности выполняется явно и независимо от других неисправностей,
188
то в нем можно использовать самые эффективные модели элементов, такие
как табличные и функциональные.
Далее сравним параллельный, дедуктивный и конкурентный методы
моделирования по следующим критериям:
1)быстродействие;
2)затраты памяти;
3)возможность использования многозначных алфавитов;
4)возможность использования функциональных моделей;
5)способность использования различных моделей задержек.
Параллельный и дедуктивный методы моделирования достаточно
эффективны в двоичном алфавите. Обобщение параллельного метода на троичный алфавит выполняется достаточно просто – при этом как мы видели быстродействие уменьшается, а затраты памяти увеличиваются в два раза. Обобщение дедуктивного метода на троичный алфавит выполняется уже сложнее и требует значительного увеличения ресурсов.
Обобщение параллельного и дедуктивного метода на многозначные алфавиты также возможно, но требует значительного увеличения вычислительных ресурсов. Структура данных и реализация алгоритмов в параллельном и дедуктивном методах существенно зависит от значности используемого алфавита моделирования.
Оба метода частично допускают использование функциональных моделей логических элементов. Это возможно только в том случае, когда функционирование элементов может быть описано с помощью булевых функций.
Напротив конкурентный метод моделирования относительно легко допускает использование многозначных алфавитов и переход на функциональный уровень: структура данных и реализация алгоритма слабо зависят от значности алфавита. Более того, этот метод допускает использование различных, в том числе более адекватных, моделей
189
задержек, поскольку в нем каждый неисправный элемент обрабатывается индивидуально.
Мы уже отмечали, что дедуктивный метод эффективнее параллельного для больших схем. Экспериментальные исследования показали, что конкурентный метод по быстродействию превосходит дедуктивный. Это обуславливается следующими факторами. В
конкурентном методе реализуется событийность не только по значениям сигналов и спискам, но и по неисправностям. В конкурентном методе активными являются только отдельные неисправные элементы, а в дедуктивном часто заново вычисляются списки неисправностей.
Недостатками конкурентного метода являются большие затраты памяти и сложность реализации алгоритма, поскольку он использует обработку больших динамичных списков.
Известны работы, в которых предпринималась попытка объединить преимущества всех трех методов.
5.5Одиночное распространение
Вразделе 5.1 мы рассмотрели метод последовательного моделирования неисправностей. Однако в тривиальном случае, когда одна неисправность моделируется на одном наборе (single pattern single fault propagation-SPSFP [44]), данный подход требует достаточно больших затрат ресурсов времени. Поэтому были разработаны стратегии,
ускоряющие данный метод. Эффективным является подход, суть которого заключается в следующем. Комбинационная схема предварительно разбивается на максимальные одновыходные подсхемы .
Определение 5.1 Максимальная одновыходная подсхема - это комбинационная древовидная схема, не имеющая разветвлений, с одним
выходом.
190
