
Tarasevich_L_S__Grebennikov_P_I__Leussky_A_I
.pdfВсе факторы производства можно представить в виде трех агрегатов: труд, капитал (орудия и средства труда, включая природные ресурсы) и уровень научно-технических знаний (научно-технический прогресс). Научно-технический прогресс является основным фактором увеличения результативности современного производства, но в отличие от труда и капитала он не имеет самостоятельной
вещественной формы и проявляется в виде совершенствования средств производства и повышения квалификации работников. Поскольку микроэкономика изучает процесс ценообразования как механизм согласования индивидуальных целей взаимосвязанных экономических субъектов в заданных условиях, то уровень развития НТП предполагается заданным1. В этом случае объем выпуска продукции (Q) зависит от количества и качества только двух совместно применяемых факторов производства – труда (L) и капитала (К), т. е. производственная функция имеет вид Q = Q(L,K). Переход к новой технологии отображается изменением оператора производственной функции – характера зависимости выпуска от объемов используемых факторов производства.
Параметры производственной функции являются натуральными величинами потока, имеющими размерность количество/время. Если, например, при оптимально организованном производстве за 1 час 5 рабочих на 3 станках изготовляют 20 деталей, то Q = 20 шт/час, L = 5 часов труда, K = 3 стако-часа. Для краткости в дальнейших примерах размерность параметров будем опускать.
Конкретный вид производственной функции устанавливается на основе наблюдений за тем, как меняется объем выпуска по мере изменения применяемых объемов труда и капитала.
Короткий и длительный периоды. Возможности изменить используемые в производстве объемы труда и капитала неодинаковы. Если спрос на продукцию фирмы возрастает, то на первых порах
увеличение производства достигается за счет дополнительного привлечения труда на те же производственные мощности, поскольку для расширения последних, как правило, требуется больше времени. В связи с этим вводятся понятия «короткий» и «длинный» периоды.
Время, в течение которого нельзя изменить объем одного из используемых в производстве факторов, называют коротким периодом. В свою очередь фактор, объем которого нельзя изменить в коротком периоде называют постоянным, а фактор, объем использования которого меняется по мере изменения выпуска, - переменным. Время, достаточное для изменения объемов обоих факторов производства, - это длинный период, и поэтому в нем все факторы являются переменными.
Соотношение между количеством выпускаемой за определенное время продукции (output) и количеством используемых для ее изготовления факторов производства (input) назовем технической результативностью производства. В коротком и длинном периодах она измеряется по-разному.
Техническая результативность производства в коротком периоде
Примем, что переменным фактором является труд. Тогда в коротком периоде у производственной функции остается одна переменная - количество используемого труда. Типичная зависимость между выпуском продукции и количеством труда, применяемого при фиксированном объеме капитала, представлена на рис. 2.1. В алгебраическом виде эта функция записывается следующим образом:
Q = aL + bL2 - cL3,
где а, в, с - технологические коэффициенты.
PDF created with pdfFactory trial version www.pdffactory.com
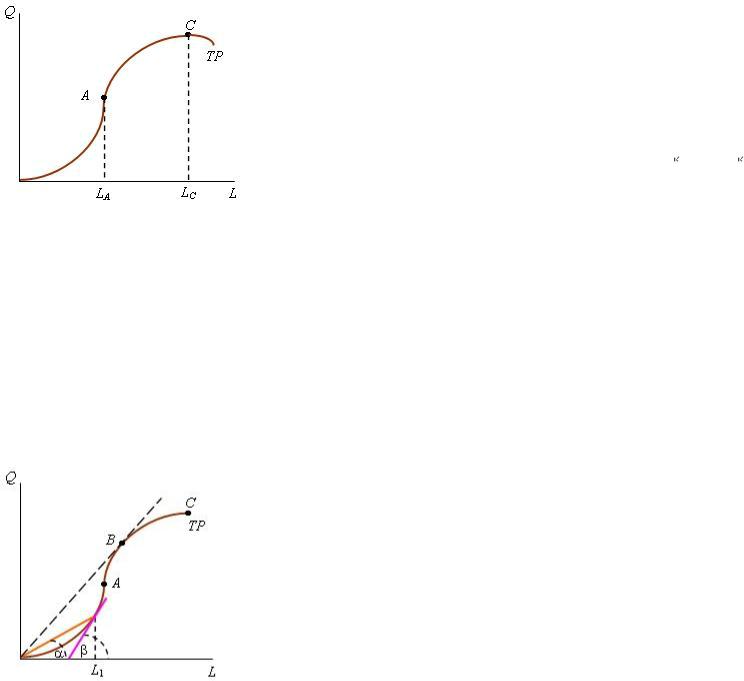
продукции |
абсцисс). После достижения определенного уровня занятости LC |
||||
|
|||||
|
общий выпуск начинает уменьшаться. Поэтому участок кривой ТР |
||||
|
за точкой С на рис. 2.1 экономисты не рассматривают. |
|
|||
|
Результат первых порции затраченного труда, присоединяемый к |
||||
|
заданному объему капитала, как правило, обеспечивает |
||||
|
увеличение |
выпуска, |
опережающее |
рост |
количества |
|
вовлекаемого в производство труда (график общего выпуска ТР |
||||
|
(total product) загибается к оси ординат). Если в цехе с двумя |
||||
|
десятками станков численность работающих возрастает с 5 до |
||||
|
10 человек, |
то выпуск, скорее всего, увеличится более, чем в |
|||
|
2 раза, а 20 рабочих могут более чем вдвое повысить объем |
||||
|
производства по сравнению с 10 рабочими. Ускоренный рост |
||||
|
выпуска продолжается до определенного соотношения /LA, где |
||||
|
- фиксированный объем капитала. При более интенсивном |
||||
|
использовании данных производственных мощностей за счет |
||||
Рис. 2.1. Кривая общего выпуска |
дальнейшего увеличения применяемого труда рост выпуска |
||||
начинает отставать от роста труда (график ТР загибается к оси |
|||||
Для количественной характеристики технической результативности производства в коротком периоде применяют три взаимосвязанных показателя: среднюю производительность, предельную производительность и эластичность выпуска по переменному фактору.
Отношение общего объема выпуска к общему количеству используемого переменного фактора (Q/L)
называют средней производительностью переменного фактора АР (average product). Графически она представляется наклоном прямой, соединяющей точки кривой ТР с началом координат. На рис. 2.2 средняя производительность труда при его использовании в объеме L1 единиц равна tg . Средняя
. Средняя
производительность труда по мере увеличения его количества при данном объеме капитала сначала повышается (на рис. 2.2 до точки В), а затем снижается.
Рис.2.2. Средняя и предельная производительности труда
Приращение общего выпуска при увеличении количества используемого труда на единицу называют предельной производительностью труда МР (marginal product).
Алгебраически она представляется как производная функции общего выпуска по труду: МРL = dQ/dL. Графически предельная производительность труда при использовании L1 единиц труда соответствует на рис. 2.2 величине tg .
.
Пока капиталовооруженность труда не достигнет величины  /LA, его предельная производительность растет быстрее средней. При
/LA, его предельная производительность растет быстрее средней. При
дальнейшем снижении капиталовооруженности труда его предельная производительность уменьшается, а средняя продолжает расти. Это приводит к тому, что оба показателя
принимают одинаковы значения при капиталовооруженности
труда 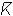 /LB. Дальнейшее увеличение количества используемого труда сопровождается снижением и средней, и предельной производительности, но общий выпуск еще некоторое время растет.
/LB. Дальнейшее увеличение количества используемого труда сопровождается снижением и средней, и предельной производительности, но общий выпуск еще некоторое время растет.
Обратим внимание на две примечательные особенности:
1.Снижение средней производительности переменного фактора начинается тогда, когда значения предельной и средней производительностей становятся равными (в точке В на рис. 2.2 tg = tg
= tg ).
).
2.После достижения определенной капиталовооруженности труда  /LA его предельная производительность монотонно снижается, т.е. начинает действовать, так называемый, «закон снижающейся предельной производительности» переменного фактора производства.
/LA его предельная производительность монотонно снижается, т.е. начинает действовать, так называемый, «закон снижающейся предельной производительности» переменного фактора производства.
На основе изменения tg и tg
и tg по мере увеличения количества используемого труда можно построить кривые его средней и предельной производительностей (рис. 2.3).
по мере увеличения количества используемого труда можно построить кривые его средней и предельной производительностей (рис. 2.3).
PDF created with pdfFactory trial version www.pdffactory.com
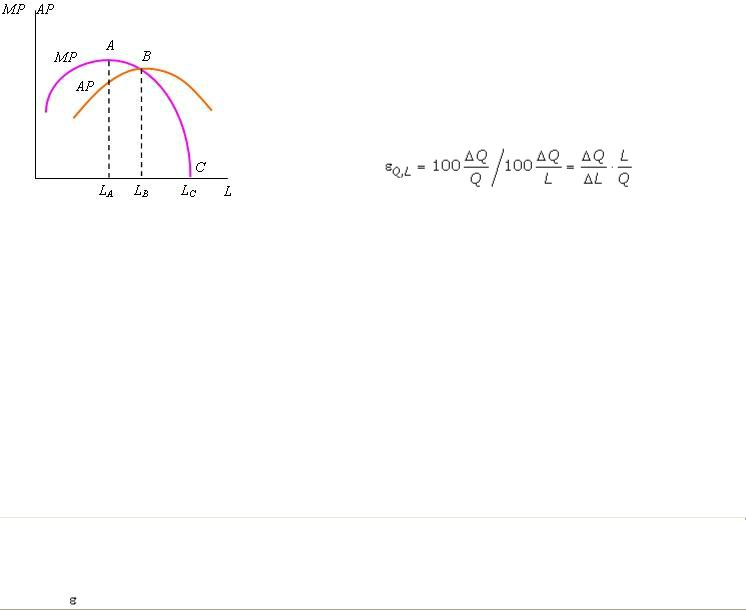
Рис.2.3. Кривые средней и предельной производительности труда
 Разобраться в этом поможет
Разобраться в этом поможет  2.1.
2.1.
Еще одной характеристикой технической результативности производства в коротком периоде служит коэффициент эластичности выпуска ( Q,L) по переменному фактору. Он показывает, на сколько процентов изменится выпуск при изменении объема переменного фактора на 1%:
Q,L) по переменному фактору. Он показывает, на сколько процентов изменится выпуск при изменении объема переменного фактора на 1%:
.
Соотношение между тремя показателями технической результативности переменного фактора производства выражается следующим равенством:
 Q,L = MPL / APL.
Q,L = MPL / APL.
Из рис. 2.3 следует, что при увеличении количества используемого труда от 0 до LB имеет место  Q,L > 1; при L = LB коэффициент
Q,L > 1; при L = LB коэффициент  Q,L = 1; в интервале LB < L < LC эластичность выпуска по переменному фактору убывает от 1 до 0, а при использовании заданного объема капитала и количестве труда больше LC коэффициент эластичности принимает отрицательное значение.
Q,L = 1; в интервале LB < L < LC эластичность выпуска по переменному фактору убывает от 1 до 0, а при использовании заданного объема капитала и количестве труда больше LC коэффициент эластичности принимает отрицательное значение.
Таким образом, техническая результативность производства в коротком периоде проходит четыре стадии (I-IV), представленные в табл. 2.1 (на рис. 2.2 и 2.3 они отделены друг от друга точками А, В
и С).
Таблица 2.1
Стадии технической результативности производства в коротком периоде
Показатель |
Стадия I |
Стадия II |
ТР |
Растет |
Растет |
AР |
" |
" |
MР |
" |
Снижается |
Q,L |
>1 |
>1 |
Стадия III |
Стадия IV |
Растет |
Снижается |
Снижается |
" |
" |
" |
{1,0} |
<0 |
Практический аспект проведенного анализа заключается в том, чтобы определить, какой объем переменного фактора целесообразно использовать в коротком периоде. Очевидно, что на стадии I надо увеличивать занятость, а переходить в стадию IV экономически нецелесообразно. Стоит ли переходить в стадии II и III? Для ответа на этот вопрос, кроме технологии, нужно знать цены производимой продукции и факторов производства. После того, как они будут введены в наш анализ, можно будет ответить на поставленный вопрос.
При использовании показателей средней и предельной производительностей, а также эластичности весь выпуск, как бы, вменяется только одному, переменному фактору. Но с не меньшим основанием результат производства можно «приписать» постоянному фактору. Его средняя производительность
APK = Q/ . Она повышается при увеличении количества применяемого труда до тех пор, пока растет общий выпуск. Но поскольку в коротком периоде решения принимают по поводу объемов использования переменного фактора, то определяют показатели его результативности.
. Она повышается при увеличении количества применяемого труда до тех пор, пока растет общий выпуск. Но поскольку в коротком периоде решения принимают по поводу объемов использования переменного фактора, то определяют показатели его результативности.
Техническая результативность производства в длинном периоде
Так как в длинном периоде меняется не только количество используемого в производстве труда, но и объем капитала, то производственную функцию в нем можно представить в виде множества производственных функций в коротком периоде, различающихся объемами капитала. Шесть таких функций приведены в табл. 2.2. В столбцах показано изменение выпуска по мере увеличения труда при фиксированных объемах капитала, а в строках - при росте капитала и неизменных объемах труда. В целом это есть табличная форма представления производственной функции в длинном периоде.
Таблица 2.2
Табличная форма производственной функции длинного периода
PDF created with pdfFactory trial version www.pdffactory.com

Количество труда |
|
|
Величина Q при К |
|
|
|
L |
10 |
20 |
30 |
40 |
50 |
60 |
50 |
33 |
40 |
44 |
47 |
50 |
52 |
60 |
38 |
46 |
50 |
54 |
57 |
60 |
70 |
43 |
51 |
57 |
61 |
64 |
67 |
80 |
48 |
57 |
63 |
67 |
71 |
74 |
90 |
52 |
62 |
68 |
74 |
78 |
81 |
Данные, приведенные в табл. 2.2, отражают «закон снижающейся предельной производительности и труда, и капитала». Это выражается в том, что значения величин в столбцах и строках растут медленнее, чем значения, отражающие увеличение соответственно количества применяемого труда и объема капитала. Эту особенность производственной функции в длинном периоде необходимо учитывать при выборе алгебраической формы ее представления. Для данной цели не подходит, например, функция вида Q = aL + bK, где а и b - константы, так как в этом случае предельные производительности факторов производства неизменны.
Типичной формой производственной функции в длинном периоде является степенная функция вида:
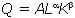 ,
,
где А,  ,
,  - положительные постоянные числа, характеризующие технологию производства.
- положительные постоянные числа, характеризующие технологию производства.
Широкое применение в экономическом анализе получила функция Кобба - Дугласа2
Табл. 2.2 представляет именно такую функцию. В ней данные округленные до целых чисел соответствуют формуле Q = L0,75K0,25.
Показатели степеней  и
и  производственной функции равны коэффициентам эластичности выпуска по факторам
производственной функции равны коэффициентам эластичности выпуска по факторам
При попытке оценить результативность производства в длинном периоде путем деления общего выпуска продукции на количество используемых факторов возникает затруднение из-за того, что нельзя суммировать число рабочих с числом станков или гектарами земли. Тем не менее определенную характеристику технологии можно получить, наблюдая за изменением выпуска при изменении объемов обоих факторов производства в одно и то же число раз, т.е. меняя масштаб производства. Результат
воздействия на выпуск пропорционального изменения обоих факторов называют эффектом масштаба
(returns to scale)3.
Рост объемов труда и капитала в n раз может сопровождаться увеличением выпуска: 1) в n раз; 2) более, чем в n раз; 3) менее, чем в n раз. В первом случае говорят, что технология имеет неизменный эффект масштаба, во втором - растущий и в третьем - снижающийся. В табл. 2.3 приведены числовые примеры для каждого из них.
|
|
|
|
|
|
Таблица 2.3 |
Технологическая результативность производства в длинном периоде |
|
|||||
|
|
|
|
|
|
|
Технология производства |
|
Объем выпуска при |
|
Эффект масштаба |
||
L = 20 |
|
L = 30 |
|
L = 40 |
||
|
К = 100 |
|
К = 150 |
|
К = 200 |
|
Q = L0,75K0,25 |
29,9 |
|
44,9 |
|
59,8 |
Постоянный |
|
(1) |
|
(1,5) |
|
(2) |
|
PDF created with pdfFactory trial version www.pdffactory.com
|
|
|
|
|
Q = L0,75K0,5 |
94,6 |
157,0 |
224,9 |
Растущий |
|
(1) |
(1,7) |
(2,4) |
|
Q = L0,5K0,25 |
14,1 |
19,2 |
23,8 |
Снижающийся |
|
(1) |
(1,4) |
(1,7) |
|
Примечание. В скобках указано, во сколько раз увеличен выпуск по сравнению с исходным.
Поскольку показатели степеней в производственной функции Q = AL K
K показывают, на сколько процентов возрастет выпуск при увеличении соответствующего фактора производства на 1%, то при
показывают, на сколько процентов возрастет выпуск при увеличении соответствующего фактора производства на 1%, то при  +
+  = 1 постоянный эффект масштаба; при
= 1 постоянный эффект масштаба; при  +
+  > 1 - растущий, а при
> 1 - растущий, а при  +
+ 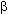 < 1 - снижающийся.
< 1 - снижающийся.
|
Для |
графического представления |
производственной |
|||
|
функции в длинном периода в двухмерном пространстве |
|||||
|
используют семейство линий равного выпуска. Линия равного |
|||||
|
выпуска, или изокванта, представляет множество различных |
|||||
|
сочетаний объемов труда и капитала, при которых достигается |
|||||
|
один и тот же объем выпуска. Из табл. 2.2 следует, что 57 ед. |
|||||
|
продукции можно выпустить при трех различных комбинациях |
|||||
|
труда и капитала: K1 = 50, L1 = 60; K2 = 30, L2 = 70; K3 = 20, |
|||||
|
L3 = 80. |
Кроме этих |
трех |
комбинаций |
труда |
и капитала |
|
существует множество других, при которых по технологии, |
|||||
|
характеризующейся производственной функцией Q = L0,75K0,25, |
|||||
|
тоже можно произвести 57 ед. продукции. Соединив все точки, |
|||||
|
представляющие эти комбинации в системе координат K,L, |
|||||
|
получим изокванту 57. Аналогично строится изокванта для |
|||||
|
любого |
другого |
объема |
выпуска, |
в |
результате |
Рис.2.4. Карта изоквант |
производственная функция в длинном периоде предстает в |
|||||
виде семейства или карты изоквант (рис. 2.4). |
|
|||||
|
|
|||||
|
Это иллюстрирует: |
|
2.2. |
|
|
|
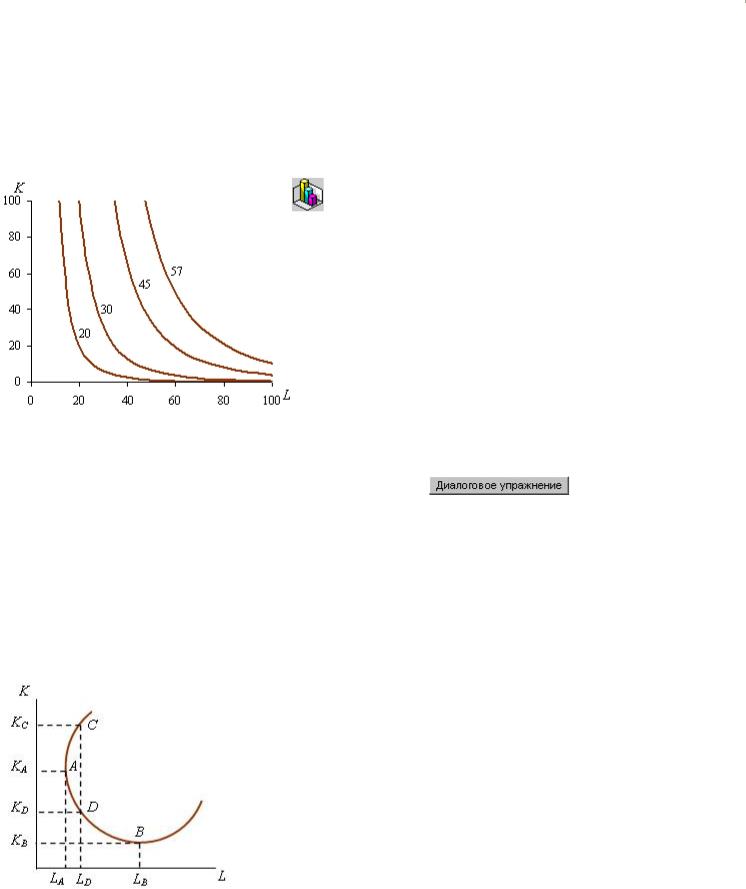
Изокванта является одним из основных инструментов графического анализа технической результативности производства. Поэтому выясним, чем определяются её конфигурация и расположение в пространстве K, L.
Рис. 2.5. Эффективная и неэффективная области изокванты
Поскольку производственная функция выражает зависимость между количеством используемых факторов и максимально возможным выпуском, то изокванта
представляет множество сочетаний минимально необходимых объемов труда и капитала для заданного выпуска. Это означает, что изокванта не может иметь положительный наклон. Допустим, что она имеет вид, изображенный на рис. 2.5. В таком случае все точки, изокванты, расположенные вне дуги АВ, представляют неэффективные варианты производства 57 ед. продукции. Так, точка С соответствует варианту производства при использовании КС единиц капитала и LС единиц труда. Но 57 единиц продукции с такими же затратами труда можно произвести, применяя лишь KD единиц капитала.
Расположение изокванты относительно осей координат определяется соотношением эластичностей выпуска по факторам производства (рис. 2.6). Если  Q,L =
Q,L =  Q,K, то изокванта симметрична биссектрисе, исходящей из начала координат. При
Q,K, то изокванта симметрична биссектрисе, исходящей из начала координат. При  Q,L >
Q,L >  Q,K она имеет относительно больший наклон к оси, на которой откладывается объем труда, а при
Q,K она имеет относительно больший наклон к оси, на которой откладывается объем труда, а при
PDF created with pdfFactory trial version www.pdffactory.com
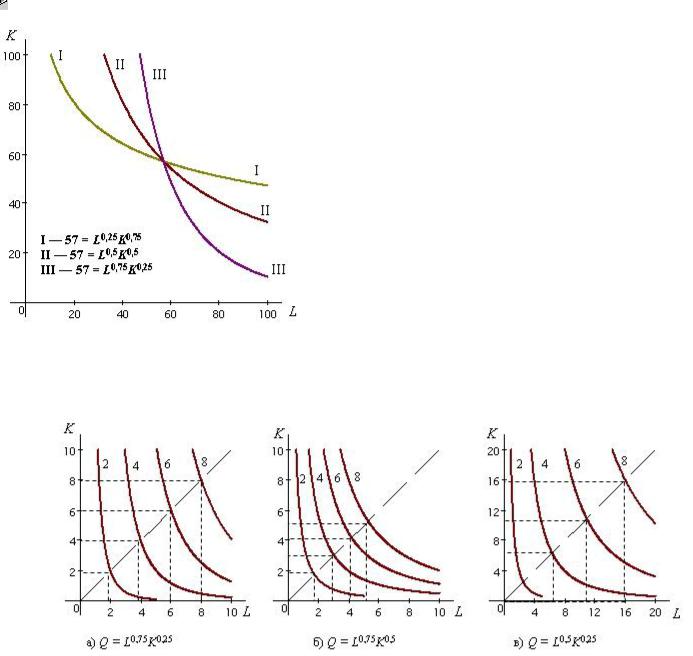
Рис. 2.6. Зависимость расположения изокванты от соотношения эластичностей выпуска по факторам производства
 Q,K >
Q,K >  Q,L, наоборот.
Q,L, наоборот.
 Проверьте это выполнив:
Проверьте это выполнив:  2.3.
2.3.
Карта изоквант наглядно отображает эффект масштаба. Изокванты, соответствующие Q = Q0, Q = 2Q0, Q = 3Q0, …, Q = nQ0, при технологии с постоянным эффектом масштаба
располагаются относительно друг друга на одинаковом расстоянии. При технологии с растущим эффектом от
масштаба они приближаются друг к другу по мере увеличения выпуска, а с уменьшающим отодвигаются
(рис. 2.7).
Изокванта свидетельствует о взаимозаменяемости факторов производства: заданный объем продукции можно
эффективно произвести при различных сочетаниях труда и капитала (различной капиталовооруженности труда). В
какой пропорции один из факторов можно заменить другим, зависит от исходной капиталовооруженности труда. Рассмотрим еще раз рис. 2.5. При переходе от сочетания КA, LА к сочетанию КD, LD на каждую
дополнительную единицу труда высвобождается больше капитала, чем при переходе от сочетания КD, LD к сочетанию КB, LB. Это связано с тем, что дуга AD имеет более крутой наклон к оси абсцисс, чем дуга DB.
Рис. 2.7. Карта изоквант при постоянном (а), растущем (б) и снижающемся (в) эффектах масштаба
(цифры около кривых - количество выпускаемой продукции)
Это иллюстрируют рис. 2.7 и:  2.4.
2.4.
Предельная норма технического замещения факторов производства
Мерой взаимозаменяемости факторов производства служит предельная норма технического замещения MRTS (marginal rate of technical substitution), которая показывает, на сколько единиц можно уменьшить один из факторов при увеличении другого фактора на единицу, сохраняя выпуск неизменным.
Предельная норма технического замещения труда капиталом
 ,
,
а предельная норма технического замещения капитала трудом
 .
.
PDF created with pdfFactory trial version www.pdffactory.com
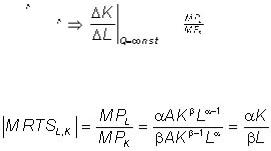
 Величина MRTS факторов производства определяется их предельной производительностью. В этом можно убедиться на основе следующих рассуждений. При увеличении количества труда на
Величина MRTS факторов производства определяется их предельной производительностью. В этом можно убедиться на основе следующих рассуждений. При увеличении количества труда на  L выпуск возрастает на
L выпуск возрастает на  L·MPL, а уменьшение объема капитала на
L·MPL, а уменьшение объема капитала на  К снижает его на
К снижает его на 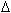 К·MPK. Следовательно, увеличение количества применяемого труда полностью компенсирует сокращение объема капитала, если выполняется следующее равенство:
К·MPK. Следовательно, увеличение количества применяемого труда полностью компенсирует сокращение объема капитала, если выполняется следующее равенство:
L·MPL = |
= = MRTSL,K. |
(2.1) |
|
К·MPK |
|||
|
|
Определим предельную норму замещения капитала трудом при технологии 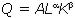 :
:
. (2.2)
При графическом построении MRTS соответствует тангенсу угла наклона касательной к изокванте в точке, указывающей необходимые объемы труда и капитала для производства заданного объема продукции.
Как конкретно меняется значение MRTS, можно увидеть, выполняя  2.5.
2.5.
В некоторых видах хозяйственной деятельности труд и капитал вообще не могут заменить друг друга и должны использоваться в фиксированной пропорции: 1 рабочий - 2 станка, 1 самолет - 10 членов экипажа. В этом случае технология производства отображается производственной функцией Леонтьева4:
Q = min{L/a; K/b},
где a и b - технологически необходимый расход соответственно труда и капитала на единицу продукции.
Если, например, на каждом автобусе дальнего следователя должно быть два водителя, то при наличии в автобусном парке 50 автобусов и 90 водителей одновременно могут обслуживаться только 45 маршрутов:
min{90/2;50/1} = 45. При технологии Леонтьева MRTS = 0.
Из равенства (2.1) следует, что при заданной технологии каждой величине капиталовооруженности труда (точке на изокванте) соответствует свое соотношение между предельными производительностями факторов производства. Иначе говоря, одной из специфических характеристик технологии является то,
как сильно меняется соотношение предельных производительностей капитала и труда при небольшом изменении капиталовооруженности. Графически это отображается степенью кривизны изокванты.
Количественной мерой этого свойства технологии является эластичность замещения факторов производства, которая показывает, на сколько процентов должна измениться капиталовооруженность труда, чтобы при изменении соотношения производительностей факторов на 1% выпуск остался неизменным. Обозначим K/L  ψ; тогда эластичность замещения факторов производства
ψ; тогда эластичность замещения факторов производства
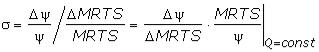 .
.
С учетом равенства (2.2) легко заметить, что  = 1 при технологии
= 1 при технологии 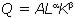 .
.
Кроме производственных функций Кобба - Дугласа и Леонтьева в экономическом анализе широко
применяют производственную функцию с постоянной эластичностью замещения факторов производства
CES (constant elasticity substitution).
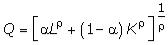 .
.
У такой функции  = 1/(1 -
= 1/(1 -  ), т.е. эластичность замены постоянна, но не обязательно равна единице. Производственные функции Кобба - Дугласа и Леонтьева являются частными случаями функции CES: если
), т.е. эластичность замены постоянна, но не обязательно равна единице. Производственные функции Кобба - Дугласа и Леонтьева являются частными случаями функции CES: если 
 0, то
0, то 
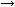 1, а если
1, а если 
 oo , то
oo , то  0.
0.
PDF created with pdfFactory trial version www.pdffactory.com
Ломанная изокванта
По технологии Кобба - Дугласа заданный объем продукции можно произвести при любой капиталовооруженности труда, по технологии Леонтьева она однозначно задана. На практике эти два крайних варианта встречаются редко. Чаще всего заданный объем продукции можно произвести при ограниченном числе различных сочетаний труда и капитала. В этих случаях от изокванты остается лишь несколько точек. Но если существуют хотя бы два варианта выпуска заданного объема продукции с постоянным эффектом масштаба, то их можно применять одновременно, производя одну часть заданного выпуска по одному варианту, а оставшуюся по другому. В результате получим множество дополнительных вариантов производства заданного объема продукции. Это множество представляет отрезок, соединяющий точки двух исходных вариантов. Рассмотрим сказанное на примере рис. 2.8.
|
Произвести 70 ед. продукции можно используя либо KA |
и |
|||||||||
|
LA, либо KB и LB. Обе технологии имеют неизменный эффект |
||||||||||
|
масштаба. Если по технологии, представленной точкой А, |
||||||||||
|
произвести |
только |
42 ед. |
продукции, |
то |
потребуется |
|||||
|
KH = 0,6KA |
единиц |
капитала |
и |
LH = 0,6LA единиц труда |
||||||
|
(точка Н). Оставшиеся 28 ед. произведем по технологии В. |
||||||||||
|
Необходимые для этого количества факторов производства |
||||||||||
|
можно |
определить |
следующим |
образом. |
Из |
точки Н |
|||||
|
проведем прямую, параллельную лучу 0В, до пересечения |
||||||||||
|
с отрезком АВ. Из |
точки |
их |
пересечения G |
проведем |
||||||
|
прямую, |
параллельную |
лучу 0А, до |
пересечения |
с |
||||||
|
лучом 0В. Точка пересечения F укажет искомые значения |
||||||||||
|
количества труда и объема капитала для производства |
||||||||||
Рис. 2.8. Использование двух |
28 ед. продукции по технологии В. Так как по построению |
||||||||||
KF + KH = KG и LH + LF = LG, то точка G наряду с точками А |
|||||||||||
технологий с постоянной отдачей от |
и В представляет один из |
множества вариантов |
выпуска |
||||||||
масштаба |
70 ед. продукции. |
|
|
|
|
|
|
|
|
||
Изменение доли заданного выпуска, производимой по каждой из двух технологий А и В, на рис. 2.8 отображается скольжением точки Н по лучу 0А. Вслед за движением точки Н точка G будет перемещаться по отрезку АВ, указывая на общие объемы труда и капитала, необходимые для производства заданного выпуска одновременно по двум вариантам. Следовательно, каждая точка на отрезке АВ представляет сочетания определенных количеств труда и капитала, позволяющих произвести заданный объем продукции.
PDF created with pdfFactory trial version www.pdffactory.com
2.6 поможет Вам разобраться в этом.
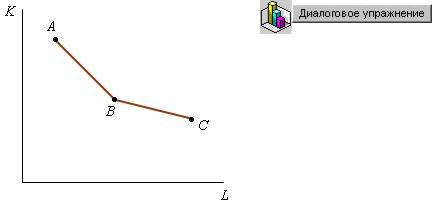
Поэтому, если, например, имеются только три варианта выпуска заданного объема продукции, представленные на рис. 2.9 точками A, B и С, то отрезки АВ и BС образуют ломанную изокванту.
На этом закончим анализ технологического соотношения «inputoutput» («ресурсы-выпуск»), который необходим, но недостаточен
для принятия фирмой решения относительно вида и масштаба производства. Экономический результат хозяйственной
деятельности определяется на основе сопоставления объемов израсходованных факторов производства и выпущенной продукции Рис. 2.9. Ломанная изокванта в ценностном измерении. При этом используют понятия «затраты
(издержки) производства», «выручка», «прибыль».
2.2. Затраты производства и функция затрат
Затраты - это ценность материалов и услуг факторов производства, использованных при изготовлении продукции. Поскольку материалы, потребленные в данном процессе производства, ранее были изготовлены при использовании труда и капитала, то в итоге все затраты сводятся к оплате факторов производства.
Когда объем производства превышает единицу, тогда различают общие затраты ТС (total cost) на весь выпуск, средние затраты АС (average cost) на единицу продукции (АС = TC/Q) и предельные затраты МС (marginal cost) - приращение общих затрат при увеличении выпуска на единицу (МС =  TC/
TC/ Q).
Q).
Зависимость между объемом произведенной продукции и минимально необходимыми для ее производства затратами называют функцией затрат.
Обозначим цену труда, т.е. количество денег, которое необходимо заплатить за использование наемного работника в течение определенного времени, rL, а цену капитала - количество денег, уплачиваемое за применение средств производства в течение некоторого времени, - rK. Тогда общие затраты на выпуск некоторого количества продукции: TC = rLL + rKK.
При заданных ценах факторов производства величина затрат определяется минимально необходимыми для выпуска продукции объемами труда и капитала, т.е. технологией, представленной производственной функцией Q = Q(L,K). Поэтому L = L(Q), K = K(Q), а следовательно, и TC = TC(Q).
Выделение короткого и длинного периодов при построении производственной функции находит свое
отражение и в функции затрат. Поскольку в коротком периоде К =  = const, то функция затрат в этом
= const, то функция затрат в этом
случае имеет вид TC(Q) = rLL(Q) + rK , т.е. в коротком периоде затраты делятся на постоянные TFC (total fixed cost), не зависящие от объема выпуска (TFC = rK
, т.е. в коротком периоде затраты делятся на постоянные TFC (total fixed cost), не зависящие от объема выпуска (TFC = rK ), и переменные TVC (total variable cost), меняющиеся по мере изменения выпуска (TVC = rLL(Q)). В длинном периоде все затраты переменные.
), и переменные TVC (total variable cost), меняющиеся по мере изменения выпуска (TVC = rLL(Q)). В длинном периоде все затраты переменные.
Переход от производственной функции к функции общих затрат осуществляется в приведенной ниже последовательности:
PDF created with pdfFactory trial version www.pdffactory.com
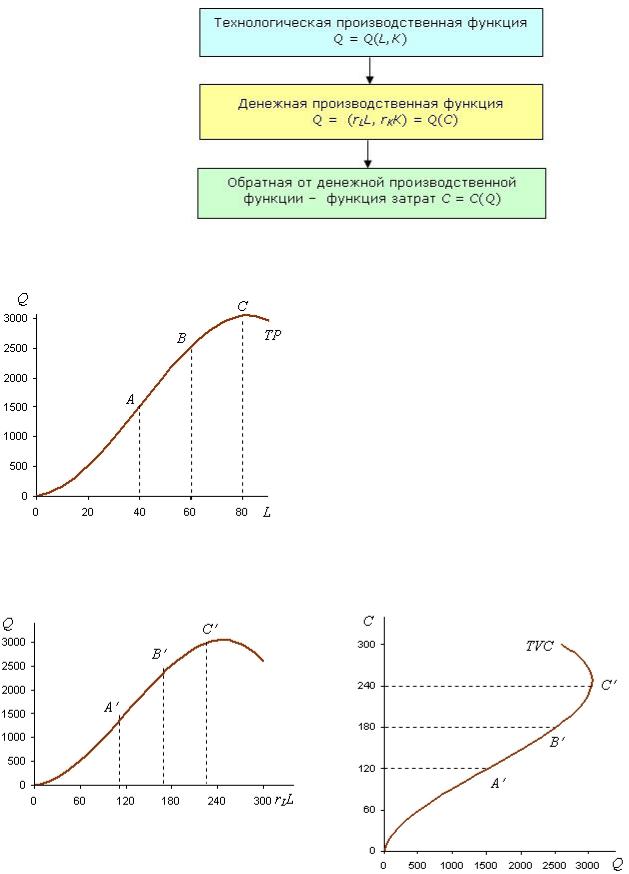
Выполним этот переход графически и алгебраически для короткого и длинного периодов.
Короткий период
Рис. 2.10. Кривая общего выпуска
в коротком периоде
Q = 6L + 1,2L2 - 0,01L3
Возьмем за основу график общего выпуска в коротком периоде, представленный на рис. 2.10.
Если на оси абсцисс откладывать не количество труда, а расходы на его оплату (rLL), то получим
график денежной производственной функции общего выпуска, изображенный на рис. 2.11 при rL = 3.
Кривая Q(rLC)  Q(C) на рис. 2.11 есть
Q(C) на рис. 2.11 есть
деформированная вследствие изменения масштаба по оси абсцисс кривая ТР на рис. 2.10: при rL > 1 она растянута, при rL < 1 - сжата. Развернув рис. 2.11 таким образом, чтобы затраты на правах функции оказались на оси ординат, получим график общих переменных затрат, изображенный на рис. 2.12. Трем особым точкам (а, в, с) на графике общего выпуска на рис. 2.11 и 2.12 соответствуют точки а', в', с'.
Рис. 2.11. Кривая денежной производственной функции
общего выпуска
Рис. 2.12. Кривая общих переменных затрат
Так как график TFC по определению - это прямая, параллельная оси абсцисс, а ТС = TFC + TVC, то график общих затрат получается в результате параллельного сдвига кривой TVC вверх на величину общих постоянных затрат (рис. 2.13).
PDF created with pdfFactory trial version www.pdffactory.com
