Електромагнетизм
12.35. До довгого тонкого провідника, розташованого в вакуумі, прикладена напруга U=5 В. Струм, який проходить по провіднику, створює в точці, що
знаходиться від нього на відстані r=1 см, магнітне поле індукцією В=5 10 4 Tл. Визначити опір провідника.
12.36. Ток силою I=20 А, протікаючи по кільцю з мідного дроту перерізом S=1 мм2, створює в центрі кільця напруженість магнітного поля Н=178 А/м. Яка різниця потенціалів U прикладена до кінців дроту, що утворює кільце?
|
|
r |
12.37. Діаметр тороїда без осердя по середній лі- |
|
|
нії дорівнює D=30 см (див. рис. 12.37). У перерізі торо- |
|
|
|
|
|
D |
їд має коло радіусом r=5 см. По обмотці тороїда, що мі- |
|
0 |
стить N=2000 витків, тече струм силою I=5 А. Корис- |
|
|
туючись законом повного струму, визначити максима- |
|
|
|
льне і мінімальне значення магнітної індукції в тороїді. |
|
|
|
12.38. По круговому витку радіусом r=5 см тече |
|
|
|
струм I=20 А. Виток розташований в однорідному маг- |
|
|
|
нітному полі, індукція якого В=40 мТл так, що нормаль |
|
Рисунок 12.37 |
до площини контуру складає кут 1= /6 з вектором ін- |
|
дукції. Визначити зміну потенціальної енергії W кон- |
|
|
|
туру при його повороті на кут = /2 в напрямку збільшення кута .
12.39.Електрон, прискорений різницею потенціалів U=300 В, рухається паралельно прямолінійному проводу на відстані r=4 мм від нього. Яка сила буде діяти на електрон, якщо по провіднику пустити струм силою I=5 А?
12.40.Протон і альфа-частинка влітають в однорідне магнітне поле перпендикулярно лініям магнітної індукції. Порівняти радіуси кіл, які описують частинки, якщо у них однакові: а) швидкості, б) енергії.
12.41.Електрон, що пройшов прискорювальну різницю потенціалів 3 кВ,
влітає в однорідне магнітне поле перпендикулярно силовим лініям. Індукція магнітного поля дорівнює 10-3 Тл. Чому рівні тангенціальне і нормальне прискорення електрона в магнітному полі?
12.42.Альфа-частинка пройшла прискорювальну різницю потенціалів U=300 В і, потрапивши в однорідне магнітне поле, стала рухатися по гвинтовій лінії радіусом r=1 см і кроком h=4 см. Визначити магнітну індукцію В поля.
12.43.Через переріз металевої пластинки товщиною b=0,5 мм йде струм I=20 А. При розміщенні пластинки в магнітному поле, перпендикулярному на-
прямку струму, виникає поперечна різниця потенціалів UH=3,1 10 6 В. Індукція магнітного поля В=1,0 Тл. Визначити концентрацію електронів провідності в металі, з якого зроблена пластинка.
12.44.У схрещені під прямим кутом однорідні магнітне поле напруженістю Н=1 106 А/м і електричне поле, напруженість якого Е=50 кВ/м, влетів іон. При якій швидкості іона (за модулем і напрямом) він буде рухатися в схрещених полях прямолінійно?
12.45.Круговий контур поміщений в однорідне магнітне поле так, що площина контуру перпендикулярна силовим лініям поля. Напруженість магнітного поля 2000 А/м. По контуру тече струм 2 А. Радіус контуру 2 см. Яку робо-
171
Електромагнетизм
ту потрібно здійснити, щоб повернути контур на кут 45 навколо осі, совпадаючої з діаметром контура?
12.46.Рамка довжиною 3 см і шириною 2 см, що містить 400 витків дроту, знаходиться в магнітному полі напруженістю 16 104 А/м. По рамці тече струм 10 7 А. Визначити магнітний момент рамки і повний магнітний потік, що пронизує рамку, якщо площина рамки становить кут 60 з напрямком магнітного поля.
12.47.Довгий циліндровий стрижень з титану поміщений в однорідне ма-
гнітне поле уздовж силових ліній. Магнітна сприйнятливість титану =1,5 10 5. Яку частину індукції сумарного магнітного поля В становить індукція магнітного поля молекулярних струмів В ?
172

Електромагнітна індукція
§13 Явище електромагнітної індукції
13.1Основні теоретичні відомості
1.Магнітний потік крізь довільну поверхню S:
|
Ф BdS . |
(13.1) |
Якщо поле однорідне B |
S |
|
const , а поверхня плоска, то |
|
|
Ф BS cos , |
(13.2) |
де – кут між нормаллю до контуру і вектором магнітної індукції B , S – площа контуру.
Потокозчеплення повний магнітний потік, зчеплений з усіма витками. У разі соленоїда або тороїда потік через кожен виток один і той же, тому
де N – повне число витків в соленоїді або тороїді.
3. Робота переміщення замкненого контура зі струмом у магнітному полі
2 |
|
A I dФ. |
(13.4) |
1 |
|
Якщо струм постійний, то |
|
A I Ф I Ф2 Ф1 , |
(13.5) |
де Ф Ф2 Ф1 – зміна магнітного потоку, який пронизує поверхню, обмеже-
ну контуром.
4. Закон електромагнітної індукції (закон Фарадея).
Ерс електромагнітної індукції пропорційна швидкості зміни повного магнітного потоку, який пронизує контур
де i – електрорушійна сила індукції; – повний магнітний потік (потокозчеп-
лення).
5. Потокозчеплення пропорційно силі струму в контурі
де L – індуктивність контура.
6. Електрорушійна сила самоіндукції S , що виникає в замкнутому контурі при зміні сили струму в ньому при L=const
I I0e R / L t ,
I I0 1 e R / L t ,
Електромагнітна індукція |
_ |
|
s L dIdt , |
(13.8) |
де L – індуктивність контура. |
|
|
7. Індуктивність довгого соленоїда’ |
|
|
L 0n2V , |
(13.9) |
де n – число витків, що припадає на одиницю довжини (щільність намотування), V – об’єм соленоїда.
8. Внаслідок явища самоіндукції в колі, що має активний опір R і індуктивність L, сила струму при замиканні і розмиканні кола змінюється не миттєво, а поступово.
Після замикання кола:
(13.10)
де I0 – усталене значення сили струму, t – час, що минув після замикання кола. Після розмикання кола:
(13.11)
де I0 – значення сили струму в колі при t=0, t – час, що минув після розмикання кола.
9. Енергія магнітного поля соленоїда
Об’ємна густина енергії магнітного поля (енергія, яка міститься в одиниці об’єму)
wм |
|
0 |
H 2 |
|
B2 |
|
|
|
|
. |
(13.13) |
|
|
|
|
|
2 |
|
2 0 |
|
13.2Алгоритми розв’язання задач та методичні поради
13.2.1.Основна задача, яке ставиться при розгляді явища електромагніт-
ної індукції, полягає в знаходженні ерс індукції i. При проведенні фізичного аналізу, перш за все, треба встановити причини зміни магнітного потоку, який пронизує контур, і те, як він змінювався. В задачах, що розглядаються в даному параграфі, будемо вважати, що контур плоский. Тоді можна виділити наступні типи задач.
1. Плоский контур розташований в однорідному змінному (нестаціонар-
ному) магнітному полі перпендикулярно лініям індукції. Якщо відомий закон зміни індукції магнітного поля B f t , то ерс індукції знаходиться наступним
чином:

Електромагнітна індукція
i d dB S , dt dt
де dBd t швидкість зміни індукції магнітного поля.
2.Плоский контур знаходиться в постійному магнітному полі, але міняється положення контура відносно поля (контур обертається в магнітному полі відносно нерухомої осі). У цьому випадку застосовують закон Фарадея у вигля-
ді (13.6).
3.Провідник (плоский контур) рухається в постійному магнітному полі,
до контуру непричому кут
змінюється. У цьому випадку зміна магнітного потоку обумовлено зміною площі, що перетинається провідником при русі. Різниця потенціалів на кінцях провідника дорівнюватиме ерс, індукованої в провіднику.
4. Розрахунок середньої ерс індукції. Залежно від причини зміни магнітного потоку використовують наступні співвідношення для знаходження зміни магнітного потоку.
При зміні індукції:
B2 B1 S cos .
При зміні положення контуру:
BS cos 2 cos 1 .
При зміні площі контуру або при перетині рухомим провідником ліній магнітної індукції:
B S2 S1 cos .
Зверніть увагу! кут між вектором магнітної індукції B і нормаллю n до контура.
5. Розрахунок заряду, що протікає по провіднику; кількості тепла, що виділився за рахунок протікання індукційного струму. Використовують метод диференціювання та інтегрування (див. §4).
13.3 Приклади розв’язання задач
Приклад 13.3.1. У магнітному полі, індукція якого змінюється за законом B B0 sin t , розташована плоска квадратна рамка зі стороною а=20 см. Пло-
щина рамки перпендикулярна вектору магнітної індукції B . Визначити ерс індукції в рамці в момент часу t=10 с, якщо В0=0,8 Тл, =15 рад/с.
Розв’язання. Причиною зміни магнітного потоку, який пронизує контур, є зміна індукції магнітного поля. Запишемо закон зміни магнітного потоку:
BS cos B0 S sin t cos , |
(1) |
де кут між вектором магнітної індукції B і нормаллю n до контуру.
Електромагнітна індукція |
_ |
Напрямок вектора магнітної B індукції збігається за напрямком з нормаллю,
тому 0 , cos0 1.
Площа S контуру:
Ерс індукції, що виникає в контурі, дорівнює швидкості зміни магнітного потоку
i d d B0 S sin t B0 S cos t . dt dt
Замінимо площу за формулою (2), отримаємо:
i B0 a2 cos t .
Підставивши чисельні значення величин у формулу (4), отримаємо
0,34 В.
Приклад 13.3.2. В однорідному магнітному полі, індукція якого В=0,1 Тл, обертається котушка, що складається з N=200 витків. Вісь обертання котушки перпендикулярна до її осі і до напрямку магнітного поля. Період обертання котушки Т=0,2 с; площа поперечного перерізу S=4 см2. Знайти максимальну ерс max в котушці, що обертається.
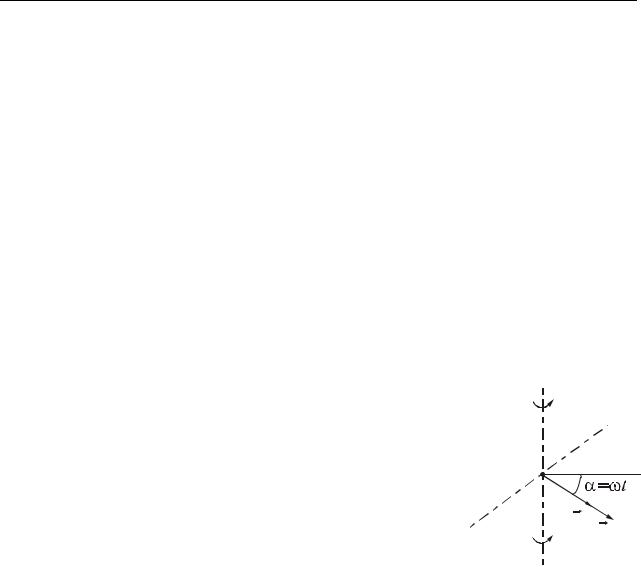
Розв’язання. Виконаємо рисунок, вкажемо напрямок ве-
ктора магнітної індукції B і напрям нормалі n до перерізу котушки (рис. 13.1). Причиною зміни магнітного потоку є зміна положення котушки в магнітному полі.
 n B
n B
Рисунок 13.1
При цьому змінюється кут між векторами B і n . |
й n збігали- |
Будемо вважати, що в початковий момент часу напрямки B |
ся. Тоді при рівномірному обертанні |
|
t , |
(1) |
де – кутова швидкість обертання.
Повний магнітний потік (потокозчеплення), зчеплений з усіма витками котушки, буде змінюватися за законом
де S площа поперечного перерізу котушки, N кількість витків. За законом Фарадея
d |
d N B S cos t |
N BS sin t . |
(3) |
dt |
dt |
|
|

|
|
|
|
Електромагнітна індукція |
де |
|
|
|
N BS max |
(4) |
Кутова швидкість і період обертання пов’язані співвідношенням |
|
2 |
. |
|
(5) |
|
|
|
T |
|
|
|
Зробимо заміну в (4), отримаємо: |
|
|
|
max 2 BS |
N . |
(6) |
|
|
T |
|
|
|
Підставивши чисельні значення величин у формулу (6), отримаємо
max 0,25 В.
Приклад 13.3.3. Провідник довжиною l=1 м рухається зі швидкістю v=5 м/с перпендикулярно лініям індукції однорідного магнітного поля. Визначити індукцію В магнітного поля, якщо на кінцях провідника виникає різниця потенці-
алів U=0,02 В.
Розв’язання. Виконаємо рисунок (рис. 13.2). Зміна магнітного потоку обумовлена зміною площі, що перетинається провідником при русі. Різниця потенціа-
Bлів на кінцях провідника дорівнюватиме ерс, що індукована в провіднику.
x v |
|
l |
|
За законом Фарадея: |
|
|
|
|
U i |
|
d |
|
. |
(1) |
|
|
|
|
|
|
|
|
|
Рисунок 13.2 |
|
|
|
|
|
|
|
|
dt |
|
|
|
Магнітний потік, що пронизує площу, яка перетинається провідником при русі, визначається співвідношенням:
де В– індукція магнітного поля;
S – площа, яку перетинає стрижень при своєму русі;
α – кут між нормаллю до площі і вектором магнітної індукції B .
α=0 , оскільки вектор магнітної індукції B збігається за напрямком з нормаллю n .
Якщо провідник рухається зі швидкістю v , то за час t він переміститься на відстань x. Площа, яку перетнуть лінії індукції при русі провідника (див. рис. 13.2):
Формули (2) і (3) підставимо в (1), отримаємо:
Електромагнітна індукція |
_ |
U d (Bldt x) Bl dxdt Blv ,
де dxdt v – швидкість, з якою рухається провідник. Таким чином,
U Blv .
З формули (5) знайдемо індукцію магнітного поля:
B Ulv .
Підставивши чисельні значення величин у формулу (6), отримаємо B 4 мТл.
Приклад 13.3.4. К Котушка з залізним осердям має площу поперечного перерізу S=20 см2 і число витків N=500. Індуктивність котушки з осердям L=0,28 Гн при струмі через обмотку I=5 А. Знайти магнітну проникність μ залізного осердя.
Розв’язання. Потокозчеплення будь-якого контуру пропорційно силі струму
LI . |
(1) |
де L – індуктивність контуру (котушки). |
|
З іншого боку, повний магнітний потік, що пронизує котушку: |
|
N . |
(2) |
Магнітний потік: |
|
BS cos , |
(3) |
де α – кут між нормаллю до площі поперечного перерізу котушки і вектором B .
α=0 , оскільки вектор магнітної індукції B збігається за напрямком з нормаллю.
Прирівняємо (1) і (2), замінивши Ф за формулою (3). отримаємо:
LI NBS . |
(4) |
З (4) знайдемо індукцію магнітного поля В: |
|
B |
LI |
. |
(5) |
|
|
NS |
|
Підставивши чисельні значення величин у формулу (5), отримаємо B 1,4 Тл.
Використовуючи графік залежності магнітної індукції В в залізі від напруженості зовнішнього поля Н, що намагнічує, наведений в довідкових матеріалах («Таблиці фізичних величин», п. 3.3.12) знайдемо відповідне значення Н:
Н≈1700 А/м.

Електромагнітна індукція
Для знаходження магнітної проникності μ використовуємо формулу зв’язку магнітної індукції В і напруженості Н:
B 0 H . |
(6) |
Виразимо з (6) магнітну проникність: |
|
|
|
|
B |
. |
(7) |
|
|
0 H |
|
Підставивши чисельні значення величин у формулу (7), отримаємо
656 .
Приклад 13.3.5. Соленоїд має N=800 витків. Переріз осердя (з немагнітного матеріалу) S=10 см2. По обмотці тече струм, що створює поле індукцією
В=8 мТл. Визначити середнє значення ерс самоіндукції 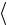 S
S  , яка виникає на за-
, яка виникає на за-
тискачах обмотки соленоїда, якщо сила струму зменшується практично до нуля за час t=0,08 с.
Розв’язання. Самоіндукція є окремим випадком явища електромагнітної індукції. Ерс самоіндукції виникає за рахунок зміни магнітного потоку Ф, створеного струмом що змінюються, який тече по соленоїду. Середнє значення ерс самоін-
дукції  S
S 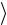 можна визначити із співвідношення:
можна визначити із співвідношення:
де N – число витків.
Струм утворює в соленоїді магнітне поле індукцією В. Зміну магнітного потоку можна знайти за формулою
де кут між напрямками вектора магнітної індукції і нормаллю до перерізу
соленоїда. =0 , cos0 =1.
Оскільки струм зменшується до нуля, то В2=0, В1=В. Підставимо рівняння (2) в (1), отримаємо:
Підставивши чисельні значення величин у формулу (3), отримаємо
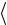 s
s  80 мВ.
80 мВ.
Електромагнітна індукція |
_ |
Приклад 13.3.6. Коло складається з котушки індуктивністю L=0,01 Гн і джерела струму. Джерело струму відключили, не розриваючи кола. Час, через який сила струму зменшиться до 0,001 початкового значення, дорівнює t=0,07 с. Визначити опір котушки.
Розв’язання. Струм, що зменшується, створює в котушці змінний магнітний потік. Зміна магнітного потоку внаслідок явища самоіндукції приводить до виникнення в котушці ерс самоіндукції. Після відключення джерела сила струму в ланцюзі буде зменшуватися за законом:
|
|
I I0e |
|
R t |
, |
|
|
|
|
L |
|
де I0 – початкове значення сили струму. |
|
|
|
|
|
|
|
|
Перетворимо рівняння (1): |
|
|
|
|
|
R |
|
|
|
I |
|
|
|
|
|
|
|
|
|
|
e L . |
|
|
|
I0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Логарифмуємо отриманий вираз: |
|
|
|
|
|
|
|
|
|
|
|
ln |
|
|
I |
|
R t . |
|
I0 |
|
|
|
|
|
|
|
L |
|
|
Знайдемо з (3) опір котушки: |
|
|
|
|
|
|
|
|
|
|
|
R |
L |
|
ln |
|
I |
. |
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
I0 |
|
Підставивши чисельні значення величин у формулу (4), отримаємо
R 0,98 Ом.
Приклад 13.3.7. Джерело струму замкнули на котушку опором R=20 Ом. Через час t=0,1 с сила струму I в котушці досягла 0,95 граничного значення. Визначити індуктивність котушки.
Розв’язання. Зростаючий струм створює в котушці змінний магнітний потік. Зміна магнітного потоку внаслідок явища самоіндукції приводить до виникнення в котушці ерс самоіндукції. При замиканні кола сила струму буде наростати за законом:
де I0 – граничне значення сили струму. Перетворимо рівняння (1):









 n
n 
 , яка виникає на за-
, яка виникає на за-
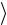 можна визначити із співвідношення:
можна визначити із співвідношення:
 80 мВ.
80 мВ.