Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Донецкий национальный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Навчальний посибник

.pdf

Скачиваний:

206

Добавлен:

03.03.2016

Размер:

2.07 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 1112 / 2512 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Електростатика

3.Якщо при взаємодії заряджених тіл відбувається перерозподіл зарядів, то запишіть закон збереження заряду.

4.При необхідності запишіть допоміжні формули і розв’яжіть отриману систему рівнянь відносно невідомої величини.

10.2.6. При розв’язанні задач на з’єднання конденсаторів в батарею, перш за все, треба встановити тип з’єднання: послідовне або паралельне. Якщо встановлено тип з’єднання, і ясно як знайти ємність батареї, то далі записуються співвідношення між зарядами і напругами.

1.Якщо плоский конденсатор підключити до джерела живлення, зарядити його і потім відключити, то при зміні ємності внаслідок розсування (зближення) його пластин, внесення (видалення) діелектрика заряд на конденсаторі не змінюється.

2.Якщо конденсатор підключений до джерела постійної напруги, то при всіх зазначених вище змінах ємності напруга між його пластинами залишається постійною.

3.Якщо між обкладинками конденсатора вставляють (або виймають) металеву пластинку, яка не замикає конденсатор, то область поля конденсатора зменшується на величину обсягу цієї платівки. Всі величини при цьому будуть змінюватися точно так само, як якщо б ми зближували (або розсовували) обкладки конденсатора.

10.3 Приклади розв’язання задач

Приклад 10.3.1. Точкові заряди q1=20 нКл і q2= 10 нКл знаходяться на відстані r=5 см один від одного. Визначити напруженість поля в точці, віддаленій на r1=3 см від першого і r2=4 см від другого заряду. Визначити також силу F, що діє в цій точці на точковий заряд q=1 нКл.

Розв’язання. Кожен заряд буде створювати своє поле незалежно від присутності

в просторі інших зарядів. За принципом суперпозиції напруженість E електри-
чного поля в точці А дорівнює геометричній сумі напруженостей E1	і E2	полів,
що створювані кожним зарядом окремо:
E E1 E2 .		(1)

q1	d		q2
B		r2	C
r1	E2
	E2
q	E		F
q	A

Рисунок 10.1

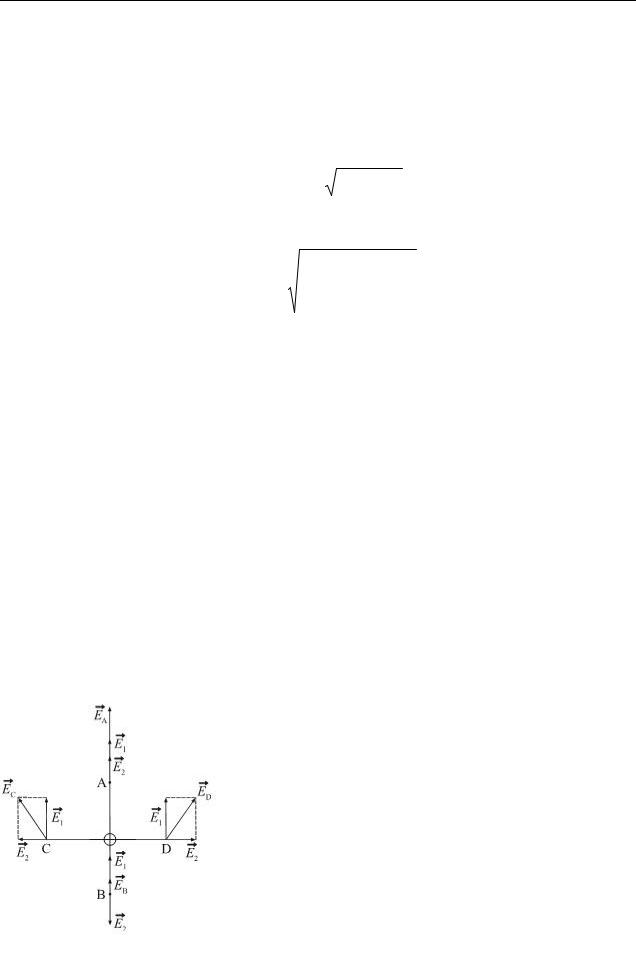
Виконаємо рисунок, вкажемо напрямки векторів E1 , E2 і E . Вектор E1 спрямований від заря-

ду q1, так як цей заряд позитивний. Вектор E2

спрямований до заряду q2, так як цей заряд негативний (див. рис. 10.1).

Заряди точкові, тому напруженості E1 і E2 можна розрахувати за формулами:

E	k	q1	,	E		k q2	,	(2)
		r 2
1					2	r 2
	1					2

111

Електростатика

де k 9 109 м/Ф – коефіцієнт пропорційності в СІ. Формули записані в припущенні, що заряди знаходяться у вакуумі ( =1).

Розглянемо АВС, утворений зарядами і точкою А. Зі співвідношення

між сторонами r 2 r 2	r 2 можна зробити висновок,							що він є прямокутним.
1	2
Отже, E1 і E2 також є сторонами прямокутника. Знайдемо модуль напруженос-
ті E за теоремою Піфагора:
	E		E2		E 2 .			(3)
				1		2
Підставимо у формулу (3) вирази для Е1 і Е2, отримаємо:
	q			2	q		2
	E k	1				2	.	(4)
	E k					2	.	(4)
	r 2				r	2
	1				2
Силу, що діє на точковий заряд, поміщений в точку А цього поля, можна
знайти, використовуючи співвідношення:
	F qE .							(5)

Напрямок сили збігається з напрямком напруженості E (див. рис.10.1), оскільки заряд q позитивний.

Підставивши чисельні значення величин у формули (4), (5), отримаємо

E 2,1 105 В/м;

F 0,21 10 3 Н.

Приклад 10.3. 2. В однорідному полі напруженістю 40 кВ/м перебуває точковий заряд 27 нКл. Знайти напруженість результуючого поля на відстані 9 см від заряду в точках, що лежать: а) на силовій лінії однорідного поля, що проходить через заряд; б) на прямій, що проходить через заряд і перпендикулярна силовим лініям.

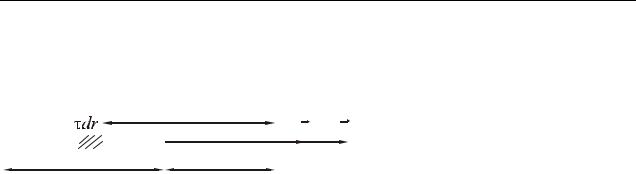
Розв’язання. а) Виконаємо рисунок (рис. 10.2), на якому вкажемо напрямок силових ліній однорідного поля й поля точкового заряду. Поле точкового заряду є центральносиметричним, тому на силовій лінії, що проходить через заряд, буде дві точки, що відстоять від заряду на відстані r. Позначимо їх через А и

В. Напруженість однорідного поля E1 , напруженість поля, створеного точковим зарядом

E2 .

За принципом суперпозиції напруженість E результуючого електричного поля дорівнює векторній сумі напруженостей E1 і E2

Рисунок 10.2

112

Електростатика

E E1 E2 .					(1)
У точці А вектори E1 й E2 спрямовані в одну сторону, тому
EA E1 E2 .					(2)
У точці В вектори E1 й E2 спрямовані в протилежні сторони, тому
EB E1 E2 .					(3)
Напрямок вектора E1 прийняли за позитивний.
Напруженість поля точкового заряду розраховується по формулі:
E	2	k	q2	,	(4)

			r 2
		2

де k 9 109 м/Ф – коефіцієнт пропорційності в СІ. Формула записана в припущенні, що середовищем є вакуум ( =1).

Проведемо проміжний розрахунок, підставивши чисельні значення у формулу (4). Одержимо: E2 30 кВ/м.

Розрахуємо напруженість результуючого поля в точках А и В, підставивши чисельні значення у формули (2) і (3). Одержимо:

EA 70 кВ/м; EB 10 кВ/м.

б) На прямій, що проходить через заряд і перпендикулярна силовим лініям, у силу симетрії також буде дві точки, що відстоять від заряду на відстані r. Позначимо їх через С и D (рис. 10.2). За принципом суперпозиції напруженість

E результуючого електричного поля дорівнює векторній сумі напруженостей

E1 і E2

E E1 E2 .

(5)

Напруженість поля точкового заряду в точках С и D однакова, тому що вони знаходяться від заряду на однаковій відстані, тому

		EC ED .				(6)
Знайдемо модуль напруженості по теоремі Піфагора:
E	C	E	D	E 2	E2 .	(7)
	C		D	1	2

Підставивши чисельні значення у формулу (7), одержимо:

EC ED 50 кВ/м.

Приклад 10.3.3. Тонкий стрижень довжиною l=20 см несе рівномірно розподілений заряд з лінійною густиною =0,1 мкКл/м. Визначити напруженість Е еле-

113

Електростатика

ктричного поля, що створюється розподіленим зарядом у точці, що лежить на осі стрижня на відстані а=20 см від його кінця.

Розв’язання. У даному випадку не можна використовувати формулу для розрахунку напруженості поля, що створюється ниткою (10.7), оскільки ця формула

	r		dE	застосовна для розрахунку поля в
			dE	E точках, що знаходяться на деякій
		a		відстані від осі нитки. У нашій за-
l		a		відстані від осі нитки. У нашій за-
				дачі точка лежить на осі. Скорис-
				дачі точка лежить на осі. Скорис-
Рисунок 10.3				таємося методом диференціюван-
Рисунок 10.3				ня та інтегрування. Для цього ро-
				ня та інтегрування. Для цього ро-

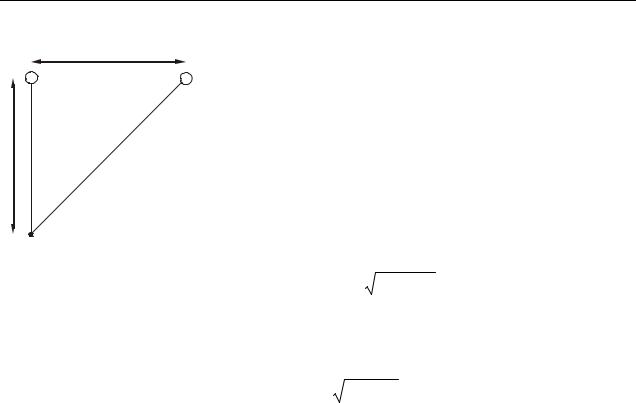
зіб’ємо стрижень на ділянки довжиною dr, настільки малі, щоб заряди dq цих ділянок можна було вважати точковими (рис.10.3). Заряд такої ділянки можна знайти наступним чином:

dq dr .

(1)

Напруженість поля, що створюється кожною малою ділянкою (такі ділянки називають елементарними), знаходимо, використовуючи формулу для розрахунку поля точкового заряду:

dE	dq		dr .	(2)
	4 0r 2	4 0
			r 2

Припускаємо, що стрижень знаходиться у вакуумі ( =1). Якщо переміщатися від кінця стрижня до його початку, то відстань від точки до елементарних

ділянок змінюється в межах від r1 a до r2 a l .

Напруженість E результуючого поля знайдемо, проінтегрувавши вираз

(2) у межах від r1 до r2. Поля елементарних ділянок спрямовані в одну сторону, тому векторну форму запису замінюємо скалярною:

					r2
				E dE .									(3)
					r1
Підставимо в (3) співвідношення (2) і інтегруємо:
E	a l		dr			1	a l			1	1
	a l		dr			1	a l			1	1
			r 2									.	(4)
												.	(4)
	a	4 0			4 0	r	a	4 0	a		a l
	a	4 0			4 0	r	a	4 0	a		a l

Підставивши чисельні значення величин у формулу (4), отримаємо

E 2,25 103 В/м.

Приклад 10.3.4. Поблизу зарядженої нескінченно протяжної площини знаходиться точковий заряд q=0,66 нКл. Заряд переміщається по лінії напруженості поля на відстань r=2 см. При цьому виконується робота A=5 мкДж. Знайти поверхневу густину заряду на площині.

114

Електростатика

Розв’язання. Припустимо, що площина заряджена позитивно. Виконаємо рису-

нок, вкажемо напрям вектора напруженості E електричного поля, створюваного площиною (рис. 10.4). З боку поля на заряд q діє сила

			Fэ qE ,				(1)
	r		де Е – напруженість електричного поля площини.
q		E	Напруженість	електричного			поля зарядженої


			площини визначається формулою:

1	F 2
1	F 2		E			,	(2)
			E		2 0	,	(2)
					2 0

	Рисунок 10.4	де поверхнева густина заряду, 0 – електрична стала,
	Рисунок 10.4	– діелектрична проникність середовища. В умові зада-
		– діелектрична проникність середовища. В умові зада-

чі не вказується середовище, в якому знаходяться заряди, тому припускаємо,

що вони знаходяться у вакуумі ( =1).

З формули (2) випливає, що напруженість поля площини не залежить від відстані. Отже, сила, що діє на заряд, є величиною постійною. Робота постійної сили може бути обчислена за формулою:

A F r cos ,

(3)

де кут між напрямком сили і переміщення. Для розглянутого випадку =0 , cos0 =1.

Підставимо вирази (1) і (2) в рівняння (3), отримаємо:

A	q	r .	(4)
	2 0

З рівняння (4) виразимо поверхневу густину заряду:

	2 0 A
	q r .	(5)

Підставивши чисельні значення величин у формулу (5), отримаємо

6,7 10 6 Кл/м2.

Приклад 10.3.5. Заряди q1=1 мкКл і q2= 1 мкКл знаходяться на відстані

d=10 см. Визначити потенціал поля в точці, віддаленій на відстань r=10 см від першого заряду, яка лежить на лінії, що проходить через перший заряд перпендикулярно напрямку від q1 до q2.

Розв’язання. Виконаємо рисунок (рис. 10.5). Позначимо точку, в якій визначається потенціал, через А. У точці А поле створюється двома точковими зарядами. За принципом суперпозиції полів потенціал результуючого поля буде дорівнювати алгебраїчній сумі потенціалів полів, створюваних кожним зарядом окремо:

115

Електростатика

2 .

(1)

Оскільки заряди точкові, то потенціали 1 і 2

мож-

на знайти, використовуючи такі формули:

(2)

де k 9 109 м/Ф – коефіцієнт пропорційності в СІ,

l – відстань між точкою А і зарядом q2 (рис. 10.4).

Заряди q1, q2 і точка А утворюють прямокут-

ний трикутник. За теоремою Піфагора:

Рисунок 10.5

r 2

d 2 .

(3)

Підставимо (2) і (3) в рівняння (1), отримаємо:

(4)

r 2 l 2

Зверніть увагу! Заряд q2 негативний, не забудьте про знак «–» при підстановці чисельних значень величин.

Підставивши чисельні значення величин у формулу (4), отримаємо

26,4 103 В.

Приклад 10.3.6. Електричне поле створене нескінченно довгою тонкою ниткою рівномірно зарядженою з лінійною густиною =20 нКл/м. Визначити різницю потенціалів двох точок цього поля, що знаходяться на відстані r1=0,5 см и r2=2 см від нитки.

Розв’язання. Поле, що створюється ниткою, не є однорідним, тому для визначення різниці потенціалів скористаємося співвідношенням, яке пов’язує напруженість і потенціал:

E d	або	d E dr .	(1)
dr

Нитка тонка, нескінченно довга, тому напруженість поля такої нитки можна знайти за формулою:

E	1		,	(2)
	2 0	r

де 0 – електрична стала, – діелектрична проникність середовища. В умові не вказується середовище, в якому знаходиться нитка, тому припускаємо, що вона

знаходиться у вакуумі ( =1). Зробимо заміну в (1), отримаємо:

116

			Електростатика
d		dr .	(3)
d	2 0	dr .	(3)
	2 0	r

Для знаходження різниці потенціалів двох точок, віддалених від нитки на відстанях r1 и r2, проінтегруємо вираз (3):

	2				r2					dr
			d							r	,	(4)
			d				2	0			,	(4)
	1				r1		2
	1				r1
	2								ln r2 .
									ln r2 .
			1			2 0				r1
Або:						2 0				r1
Або:									ln r2 .
				2								(5)
												(5)
		1				2 0				r1
						2 0				r1

Значення електричної сталої визначається за таблицею «Основні фізичні постійні», п. 3.1. Підставивши чисельні значення величин у формулу (5), отримаємо

1 2 499 В.

Приклад 10.3.7. Мідна кулька радіусом R=0,5 см поміщена в масло, густина масла м=0,8 103 кг/м3. Знайти заряд q кульки, якщо в однорідному електричному полі вона виявилася зваженою у маслі. Електричне поле спрямоване вертикально вгору і його напруженість Е=3,6 МВ/м.

Розв’язання. На заряджену кулю, що знаходиться в однорідному електричному полі будуть діяти: сила тяжіння mg – з боку Землі, сила, що виштовхує FA – з

боку рідини (сила Архімеда) і сила Fэ – з боку електричного поля. Виконаємо

рисунок (рис. 10.6), вкажемо напрям напруженості електричного поля і сили, що діють на кульку.

Шар знаходиться в рівновазі. За умовою рівноваги сума діючих сил повинна дорівнювати нулю:

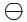F E A

mg y

Рисунок 10.6

mg FA Fэ 0 .				(1)
Запишемо рівняння (1) в проекції на вісь 0y:
mg Fэ FА 0 .				(2)
Запишемо рівняння для сил. Сила тяжіння:
mg	Vg	4	R3 g ,	(3)
	Cu	Cu 3

де Cu густина міді, V 43 R3 – об’єм кулі.

117

Електростатика

Сила, що діє на заряд з боку електричного поля:

Fэ qE ,

(4)

де q – заряд кулі, Е напруженість електричного поля. Сила Архімеда:

FA мVg м	4	R3 g ,	(5)
	3

де м – густина масла.

Формули (3), (4), (5) підставимо в (2), отримаємо наступне рівняння:

Cu	4	R3 g м			4	R3 g qE 0 .	(6)
З рівняння (6) знайдемо заряд q:	3				3
З рівняння (6) знайдемо заряд q:			R3 g
q	4		R3 g	Cu м .			(7)
q	3		E	Cu м .			(7)
	3		E

Значення густини міді визначаємо за довідковими даними: «Таблиці фізичних величин», п. 3.3.2. Підставивши чисельні значення величин у формулу (7), отримаємо

q 11,6 10 9 Кл.

Приклад 10.3.8. Електрон, що має кінетичну енергію Wк =10 еВ, влетів в однорідне електричне поле в напрямку силових ліній поля. Яку швидкістю буде мати електрон, якщо він пройде в цьому полі різницю потенціалів U=8 В?

Розв’язання. Електрон рухається уздовж силової лінії (лінії напруженості електричного поля). Силові лінії спрямовані від «+» до «–» (рис. 10.7). Отже, електрон повинен зменшити свою швидкість і, відповідно, кінетичну енергію. За теоремою про зміну кінетичної енергії можна записати:

mv2

21 ,

(1)

де А

– робота всіх сил, що діють на електрон, m

– маса

електрону, v1 – початкова швидкість електрона, v2 – кін-

Рисунок 10.7

цева швидкість.

Гальмування електрона відбувається за рахунок си-

ли, що діє з боку електричного поля. Робота сил електричного поля:

A q 1 2 qU ,

(2)

де q – заряд електрона.

Врахуємо, що

mv2

(3)

к1

118

			Електростатика
Зробимо заміну в (1) швидкість, отримаємо:
qU mv22	W	.	(4)
2	k1
2
Виразимо з (4) швидкість v2:


v2	2 Wк1	A	2 Wк1	qU	.	(5)
	m		m

Зверніть увагу! Заряд електрона негативний, не забудьте про знак «–» при підстановці чисельних значень величин.

Підставивши чисельні значення величин у формулу (5), отримаємо v2 0,84 106 м/с.

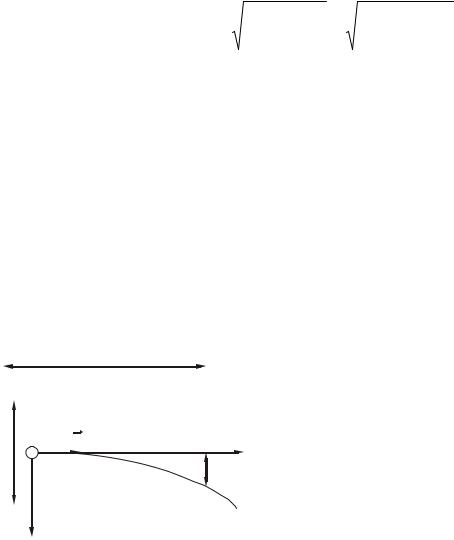
Приклад 10.3.9. Електрон влетів у простір між пластинами плоского конденсатора зі швидкістю v0=10 Мм/с, спрямованою паралельно пластинам. На скільки відхилиться електрон від початкового напрямку за час руху всередині конденсатора (поле вважати однорідним), якщо відстань d між пластинами дорівнює 16 мм, різниця потенціалів U=30 В, довжина l пластин дорівнює 6 см?

Розв’язання. На електрон, що влетів в конденсатор, буде діяти електричне поле,

яке викривляє його траєкторію. Виконаємо рисунок (рис. 10.8). Введемо систе-

му координат x0y, поєднавши початок відліку з

положенням електрона в момент попадання

його в електричне поле. Вважаємо, що сили

опору руху відсутні. У цьому випадку елект-

рон буде рухатися вздовж осі 0х з постійною

швидкістю v0, тобто рівномірно. Уздовж осі 0y

він рухатиметься рівноприскорено, так як на

нього діє постійна сила з боку електричного

поля. Таким чином, рух електрона буде анало-

гічним руху тіла, кинутого горизонтально.

Рисунок 10.8

Запишемо рівняння кінематики. Врахує-

мо, що в момент вильоту з конденсатора коор-

дината х дорівнює довжині пластин.

x l v0 t ,

(1)

(2)

Сила, що діє на електрон з боку електричного поля:

F qE .

(3)

119

Електростатика

Напруженість Е однорідного електричного поля пов’язана з різницею по-

тенціалів співвідношенням:
E U .	(4)
d
За другим законом Ньютона:
F ma .	(5)

Зробимо заміну в рівнянні (3), отримане співвідношення підставимо в (5), отримаємо:

ma qU .						(6)
			d
Знайдемо прискорення а:
a qU .						(7)
Виразимо з рівняння (1) час		md
Виразимо з рівняння (1) час		l
t		l	.			(8)
t			.			(8)
	v0
Підставимо в рівняння (2) формули (7) і (8) і знайдемо відхилення електрона:
y		qU		l 2	.	(9)
y		2md		v02	.	(9)
		2md		v02

Підставивши чисельні значення величин у формулу (9), отримаємо y 5,9 мм.

Зверніть увагу! Якщо в момент попадання в конденсатор електрон знаходився на відстані, меншій ніж 5,9 мм від позитивної пластини, то він впаде на неї перш, ніж покине конденсатор.

Приклад 10.3.10. До плоского конденсатора, у якому діелектриком служить слюда ( =7,5) прикладена напруга U=1000 В. Відстань між пластинами d=1,00 мм, площа пластин 100 см2. Визначити енергію електричного поля конденсатора й густину енергії електричного поля.

Розв’язання. Енергія електричного поля, створеного в конденсаторі, може бути визначена зі співвідношення:

W	CU 2	,	(1)
	2

де С – електроємність конденсатора, U – напруга, що прикладена до пластин. Електроємність плоского конденсатора розраховується за формулою:

120

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 1112 / 2512 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
30.04.20195.53 Mб8му_17.06.doc
#
03.03.20161.03 Mб8МУ_20-44-2011-15_Ковалёва_Шипович_Лукьяненко.pdf
#
03.03.20161.32 Mб33МУ_КГ.doc
#
03.03.2016577.54 Кб15МУ_ПУ.doc
#
03.03.2016909.97 Кб34МУ_ТОБ_2013_БС_ТТР.pdf
#
03.03.20162.07 Mб206Навчальний посибник.pdf
#
03.03.20161.98 Mб151навчатьный посибник 2.pdf
#
03.03.2016177.15 Кб4налоги.docx
#
03.03.20163.85 Mб118Научное помсобие 1All Tom 1 UA.pdf
#
03.03.20163.77 Mб174Научный пособник том 2All Tom 2 UA.pdf
#
03.03.201614.29 Mб48НГ_МУ_6_35.pdf