
Навчальний посибник
.pdf
Молекулярна фізика
8.18. Посудину, що містить газ під тиском 1,4 105 Па, з’єднали з порожньою посудиною об’ємом 6 л. Після цього в обох посудинах встановився тиск 105 Па. Знайти об’єм першої посудини, якщо температура весь час залишалася
постійною. |
p, МПа |
|
|
|
|
2 |
|
|||
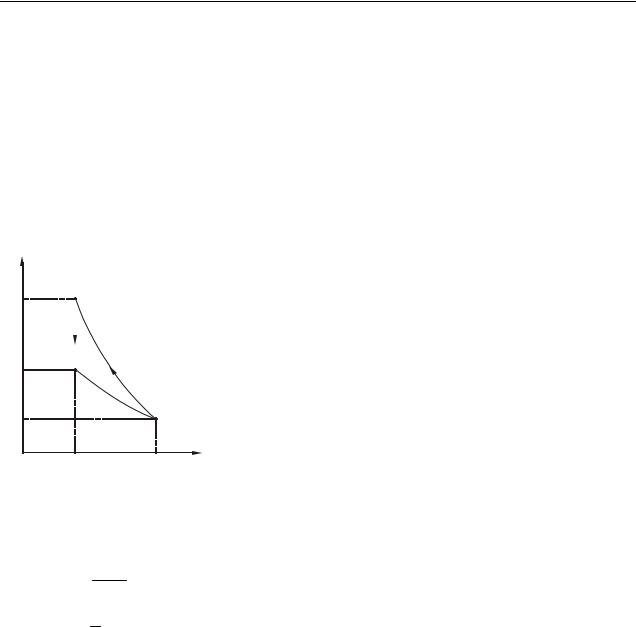
8.19. Ідеальний газ, здійснює цикл, зобра- |
|
|
|
|
|
|||||
жений на рис. 8.19. З яких процесів складається |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
цикл? Побудуйте цей цикл в координатах (p,V). |
2 |
|
|
|
|
|
|
|
|
|
8.20. У балоні об’ємом 5 л міститься ки- |
|
|
|
1 |
|
|
3 |
|
||
|
|
|||||||||
сень масою 20 г. Визначити концентрацію моле- |
1 |
|
|
|
|
|
|
|
|
|
кул в балоні. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8.21. Газ при температурі 36 С і тиску |
0 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|||||
200 400 600 |
|
T, K |
||||||||
0,7 МПа має густину 12 кг/м3. Визначити моля- |
|
|||||||||
|
|
|
|
Рисунок 8.19 |
||||||
рну масу газу. |
|
|
|
|
||||||
8.22. Колба об’ємом 4 дм3 містить деякий газ масою 0,6 г під тиском 200 кПа. Визначити середню квадратичну швидкість молекул газу.
8.23.Знайти середню довжину вільного пробігу молекул водню при тиску р=0,1 Па і температурі Т=100 К.
8.24.У посудині знаходиться вуглекислий газ, густина якого 1,7 кг/м3. Середня довжина вільного пробігу молекул 52 нм. Знайти ефективний діаметр молекул вуглекислого газу.
8.25.Знайти середнє число зіткнень в одиницю часу молекул азоту при
температурі 27 C і тиску 50 кПа.
8.26.Знайти коефіцієнт дифузії водню при нормальних умовах, якщо середня довжина вільного пробігу молекул дорівнює 16 нм.
8.27.Знайти коефіцієнт теплопровідності повітря при тиску 100 кПа і те-
мпературі 10 C. Ефективний діаметр молекул повітря вважати рівним 0,36 нм. 8.28. Знайти коефіцієнт в’язкості кисню при нормальних умовах.
Достатній рівень
8.29. Знайти молярну масу М суміші кисню масою m1=25 г і азоту масою m2=75 г.
8.30.Який об’єм займає суміш, що складається з 0,28 кг азоту и 0,04 кг гелію при температурі t= 13 С і тиску p=9,8 104 Па?
8.31.У балоні знаходиться газ при температурі t1=40 С і тиску p1=1,6 107 Па. Визначити тиск p2 в балоні після того, як 30% маси газу було використано, а температура стала t2=7 С.
8.32.Гранично допустима концентрація молекул парів ртуті в повітрі до-
рівнює 3 1016 м 3. Знайти, при якій масі речовини в одному кубічному метрі повітря з’являється небезпека отруєння.
8.33. Який тиск газу, якщо його густина 1,35 кг/м3, а середня квадратична швидкість молекул 500 м/с?
91

Молекулярна фізика
8.34.Середня квадратична швидкість молекул деякого газу за нормальних
умов дорівнює vкв =450 м/с. Скільки молекул міститься в масі m=1 г цього газу?
8.35.Повітря нагріли на Т=3 К, при цьому його об’єм збільшився на 1% від початкового. Яка була початкова температура, якщо в процесі нагрівання тиск не змінювався?
8.36.Манометр на автомобільній камері при температурі t1= 13 С показує тиск 0,160 МПа (надлишкове над атмосферним). Яким став тиск, якщо в ре-
зультаті тривалого руху автомобіля повітря в камері нагрілося до 37 С?
8.37. Манометр на балоні з газом в приміщенні з температурою t1=17 С показує тиск р=0,24 МПа (надлишкове над атмосферним). На вулиці показання манометра зменшилося на р=0,04 МПа. Знайти температуру повітря на вулиці, якщо атмосферний тиск р0=0,1 МПа.
8.38.На якій висоті тиск повітря зменшується в 5 разів? Температуру повітря t вважати постійною і рівною 17 С.
8.39.На якій висоті густина повітря становить 25% від його густини на
рівні моря? Температуру повітря t вважати постійною і рівною 0 С.
8.40. Вважаючи повітря ідеальним газом, розрахувати на якій висоті над поверхнею Землі концентрація молекул кисню в е разів менше, ніж у поверхні Землі. Температуру вважати постійною і рівною t=15 С. е – основа натуральних логарифмів.
8.41.Знайти густину повітря на висоті 4 км від поверхні Землі. Температуру повітря t вважати постійною і рівною 0 С. Тиск повітря біля поверхні Землі р0=100 кПа.
8.42.Знайти середнє число зіткнень молекули кисню протягом t=1 с при нормальних умовах.
8.43.Площа поперечного перерізу мідного стрижня S=10 см2, довжина
стрижня l=50 см. Різниця температур на кінцях стрижня Т=15 К. Яка кількість тепла проходить в одиницю часу через переріз стрижня? Втратами тепла крізь бічну поверхню знехтувати.
8.44.Яку кількість тепла втрачає за 1 хв кімната розміром 4х5 м2 і завви-
шки 3 м через чотири цегляні стіни? Температура в кімнаті t1=15 С, температура зовнішнього повітря t2= 20 С. Товщина стін 50 см. Теплопровідність цегли 0,84 Вт/(м К). Втратами тепла через підлогу і стелю знехтувати.
8.45.Два однакових сталевих моста повинні бути побудовані один на пів-
ночі, інший на півдні. Якими мають бути при 0 С зазори, що компенсують подовження мосту при зміні температури, якщо на півдні можливі коливання від
10 до +50 С, а на півночі від 50 до +20 С? При 0 С довжина моста l0=100 м. Коефіцієнт лінійного розширення сталі 1 10 5 К 1.
92

Термодинаміка
§9 Термодинаміка 9.1 Основні теоретичні відомості
Характеристиками процесів теплопередачі і виконання роботи є кількість тепла Q і робота А. Теплопередача відбувається в результаті взаємодії атомів або молекул, тобто на мікрорівні. Робота виконується в результаті взаємодії макротіл, тобто на макрорівні.
1. Перший закон термодинаміки: Кількість тепла, що передане системі, йде на приріст внутрішньої енергії системи і на виконання системою роботи над зовнішніми тілами.
|
Q U A . |
(9.1) |
|||||
Перший закон термодинаміки в диференціальній формі: |
|
||||||
|
Q dU A. |
(9.2) |
|||||
2. Внутрішня енергія ідеального газу |
|
||||||
U |
m |
|
i |
RT |
m |
CvT , |
(9.3) |
|
|
|
|||||
|
M 2 |
M |
|
||||
де i – число ступенів свободи молекули.
Для одноатомної молекули жорстким зв’язком i=3, для двоатомної i=5. Якщо число атомів в молекулі три і більше трьох, то число ступенів свободи i=6.
3. Робота розширення газу в загальному випадку:
|
|
|
|
|
V2 |
|
|
|
|
|
|
|
|
||||
|
|
|
A pdV . |
|
|
|
(9.4) |
||||||||||
|
|
|
|
|
V1 |
|
|
|
|
|
|
|
|
||||
При ізобарному процесі: |
|
A p(V2 V1 ) , |
|
|
|
(9.5) |
|||||||||||
при ізотермічному процесі: |
|
|
|
|
A |
|
m |
|
RT ln V2 |
, |
(9.6) |
||||||
|
|
|
|
|
M |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
V |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
при адіабатному процесі: |
|
A U |
m |
CV T , |
(9.7) |
||||||||||||
|
|
|
|||||||||||||||
або |
|
|
|
|
|
|
|
|
M |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
m |
|
RT1 |
|
|
|
|
|
|
|
|||||||
A |
|
V1 |
|
|
|
|
|||||||||||
|
|
|
|
1 |
V |
|
|
, |
|
(9.8) |
|||||||
M |
1 |
|
|||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
де CP – показник адіабати.
CV
93

Термодинаміка
4. Молярні теплоємності ідеального газу при постійному об’ємі (Сv) і постійному тиску (СP)
|
Cv |
i |
R , |
(9.9) |
||||||
|
||||||||||
|
|
|
2 |
|
|
|
|
|||
CP |
|
i 2 |
R . |
(9.10) |
||||||
|
|
|||||||||
|
|
|
2 |
|
|
|
||||
Зв’язок між питомою c і молярною C теплоємностями |
|
|||||||||
c |
C |
. |
|
|
(9.11) |
|||||
|
|
|
||||||||
|
|
|
M |
|
|
|
||||
Рівняння Майєра: |
|
|
|
|
|
|
|
|
||
CP Cv R . |
(9.12) |
|||||||||
5. Рівняння Пуассона, що зв’язує параметри ідеального газу при адіабат- |
||||||||||
ному процесі: |
|
|
|
|
|
|
|
|
||
|
pV const . |
|
||||||||
Для двох станів: |
|
|
|
|
|
|
|
|
||
|
p2 |
|
|
|
|
|
|
|||
|
|
|
|
|
||||||
|
|
|
V1 |
|
|
(9.13) |
||||
|
p |
|
|
|||||||
|
V |
. |
||||||||
1 |
|
|
2 |
|
|
|
||||
Зробивши заміну в рівнянні (9.13), його можна записати наступним чином:
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
p2 |
|
|
|
|
|
|
|
|
|
|
||||||
T2 |
V1 |
|
|
або |
T2 |
|
|
|
|
||
|
p |
|
|
||||||||
T |
V |
2 |
|
|
T |
|
. |
||||
1 |
|
|
|
|
1 |
|
1 |
|
|
|
|
6. Коефіцієнт корисної дії (ккд) теплової машини: |
|
||||||||||
|
|
|
|
|
Q1 Q2 . |
|
|
|
|
(9.14) |
|
|
|
|
|
|
Q |
|
|
|
|
|
|
При цьому |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
Q1 Q2 A , |
|
|
|
|
(9.15) |
|||
|
|
|
|
|
|
|
|
||||
де Q1 – кількість тепла, що одержується робочим тілом від тепловіддавача; Q2 – кількість тепла, що віддається робочим тілом теплоприймачу;
А – робота, що здійснюються робочим тілом. Ккд циклу Карно
T1 T2 , |
(9.16) |
T1
де T1 и T2 – термодинамічні температури тепловіддавача і теплоприймача.
94

Термодинаміка
7. Другий закон термодинаміки: ентропія замкнутої системи за будь-яких процесів, що відбуваються в ній не зменшується – вона зростає при необоротних процесах і залишається постійною у випадку оборотних процесів, тобто
S 0. |
(9.17) |
Зміна ентропії системи в будь-якому оборотному процесі, що переводить її з рівноважного стану 1 в рівноважний стан 2:
|
|
|
|
|
2 |
Q |
|
|
S S |
|
S |
|
|
1 |
обр |
. |
(9.18) |
2 |
1 |
|
||||||
|
|
|
T |
|
||||
|
|
|
|
|
|
|
||
9.2Алгоритми розв’язання задач та методичні поради
9.2.1.Перш за все, треба з’ясувати характер процесу, що протікає в газі, якщо він не вказаний в умові завдання. Для ізобарного процесу виконується умова p const , для ізохорного – V const , для ізотермічного – T const , для
адиабатного – Q 0 .
Для виконання ізотермічного процесу необхідно повільне протікання процесу. Близькими до адіабатного процесу є процеси яки протікають швидко, оскільки кількість тепла, яким обмінюється тіло з зовнішнім середовищем, буде тим менше, чим швидше протікає процес.
9.2.2. Основна задача термодинаміки рівноважних процесів полягає в знаходженні всіх макростанів фізичної системи. Якщо початковий і кінцевий стани системи відомі, то можна знайти зміну її внутрішньої енергії. Для ідеального газу в цьому випадку використовують формулу (9.3).
Якщо процес відомий, то можна знайти роботу, що виконана системою, розрахувати кількість тепла, що отримане або віддане системою, використовуючи формули (9.4) – (9.8), а також перший закон термодинаміки – формули
(9.1), (9.2).
9.2.3. При розрахунку зміни ентропії за формулою (9.18) треба пам’ятати, що Q означає кількість тепла, яке отримане тілом. Якщо тіло віддає тепло, то
Q пишуть зі знаком мінус. Якщо перехід з початкового стану в кінцеве здійс-
нюється декількома процесами, то зведена кількість тепла дорівнює їх алгебраїчній сумі у кожному процесі. Формулу (9.18) можна застосовувати тільки до оборотних процесів.
9.3. Приклади розв’язання задач
Приклад 9.3.1. Ідеальний газ переходить зі стану 1 в стан 2 (рис. 9.1): а) по ділянці 1А2; б) по ділянці 1ВCD2. Вкажіть характер процесу на кожній ділянці. У якому випадку газ виконує більш велику роботу і в скільки разів?
Розв’язання. Розглянемо ділянку 1А2. Віна складається з двох процесів. Перехід 1А відповідає ізохорному процесу, оскільки об’єм постійний, перехід А2 – ізобарний, оскільки тиск постійний. При ізохорному процесі робота дорівнює
95

Термодинаміка
нулю, так що об’єм залишається постійним: A1A 0 . Отже, робота при переході
газу із стану 1 в стан 2 по ділянці 1А2 буде дорівнювати роботі на ділянці А2. Робота при ізобарному процесі чисельно дорівнює площі, обмеженій графіком процесу і ординатами об’єму. З графіка визначаємо: р=1 МПа=106 Па,
V1=10 л =10 10–3 м3, V2=40 л =40 10–3 м3.
Розрахуємо роботу:
A1A2 106 40 10 10 3 30 103 Дж.
Розглянемо ділянку 1ВCD2. Вона складається з чотирьох процесів. Переходи
1В і СD відповідають ізобарним процесам, так |
p, МПа |
|
|
|
|
|
|
|
|
|
||||
вони відбуваються при постійних тисках. Пере- |
1 |
|
|
B |
|
|
||||||||
ходи ВС і D2 відповідають ізохорним процесам, |
|
3 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|||||
оскільки вони відбуваються |
при |
постійних |
|
2 |
|
|
|
|
|
C |
|
D |
||
об’ємах. Отже, робота при переході газу із ста- |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
||||
ну 1 в стан 2 по ділянці 1ВCD2 дорівнюватиме |
|
1 |
|
|
A |
|
|
|
2 |
|||||
|
|
|
|
|
|
|||||||||
сумі робіт на ділянках 1В і СD. З графіка визна- |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
||||
чаємо: на ділянці 1В р=3 МПа=3 106 Па, V =10 л |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
0 10 |
20 30 |
40 V, л |
||||||||||
=10 10–3 м3, V2=20 л =20 10–3 м3. |
|
1 |
|
|
||||||||||
|
|
|
|
|
|
|
Рисунок 9.1 |
|
|
|||||
Розрахуємо роботу на ділянці 1В: |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
A |
3 106 |
20 10 10 3 30 103 |
Дж. |
|
|
|
|
|
||||||
1B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
З графіка визначаємо: на ділянці СD |
р=2 МПа=2 106 |
Па, V1=20 л =20 10–3 м3, |
||||||||||||
V2=40 л=40 10–3 м3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Розрахуємо роботу на ділянці СD:
ACD 2 106 40 20 10 3 40 103 Дж.
Робота на ділянці 1ВCD2:
A1BCD2 30 40 103 70 103 Дж.
Знайдемо відношення робіт:
A |
70 |
103 |
|
|
1BCD2 |
|
30 103 |
2,33 . |
|
|
||||
A1A2 |
|
|||
Приклад 9.3.2. Деяка маса кисню займає об’єм V1=3 л
при температурі t1=27 С і тиску p1=820 кПа (рис. 9.2). У стані В газ має параметри V2=4,5 л і p2=600 кПа. Знайти кількість тепла Q, що отримане газом, роботу А, що виконана газом при розширенні, і зміну U внутрішньої енергії газу, якщо він переходить зі стану А в стан В: а) по ділянці АСВ; б) по ділянці АDВ.
Розв’язання. а) Розглянемо перехід по ділянці АСВ. Цей
p p |
A |
D |
|
||||
1 |
|
|
|
|
|
|
|
p |
|
|
|
|
|
B |
|
C |
|
|
|||||
2 |
|
|
|||||
|
V1 |
V2 |
V |
||||
Рисунок 9.2 |
|
|
|
||||
96

Термодинаміка
перехід складається з двох процесів: ділянка АС – ізохорний процес при V1=const, ділянка СВ – ізобарний процес при р2=const. На ділянці АС об’єм не змінюється, тому робота з розширення газу дорівнює нулю. Отже, робота, що здійснюється газом на ділянці АСВ, буде дорівнювати роботі, яка виконується на ділянці СВ. Процес ізобарний, тому
A p2 (V2 V1) . |
(1) |
Внутрішня енергія є функцією стану. Це означає, що її зміна не залежить від того, як здійснювався перехід, а буде визначатися тільки значеннями температури в початковому і кінцевому станах. Позначимо температуру кінцевого стану (стану В) через Т2. тоді
U |
m i |
R T |
T |
i |
|
m |
RT |
|
m |
RT |
|
, |
(2) |
||
|
|
|
|
|
|
||||||||||
M 2 |
2 |
|
M |
||||||||||||
|
2 |
1 |
M |
2 |
|
1 |
|
|
|
||||||
де i – число ступенів свободи. Кисень – двоатомний газ, тому i=5. Для станів А і В запишемо рівняння Менделєєва – Клапейрона:
p V |
|
m |
RT , |
(3) |
|||
|
|
||||||
1 |
1 |
|
M |
1 |
|
||
|
|
|
|
|
|||
p V |
|
|
m |
RT . |
(4) |
||
|
|
||||||
2 |
2 |
|
|
M |
2 |
|
|
|
|
|
|
|
|
||
Зробимо заміну в (2) з урахуванням рівнянь (3) і (4), отримаємо:
U |
i |
p V |
2 |
p V . |
(5) |
|
|
||||||
2 |
2 |
1 |
1 |
|
||
|
|
|
|
|
||
Кількість тепла, що отримане газом, розраховується за першим законом термодинаміки:
Q U A . |
(6) |
Підставивши чисельні значення величин у формули (1), (2), (6) отримаємо:
A 900 Дж, U 600 Дж, Q 1500 Дж.
б) Розглянемо перехід по ділянці АDВ. Він теж складається з двох процесів: АD
– ізобарний процес при р1=const, DВ – ізохорний процес при V2=const. Робота на ділянці DВ дорівнює нулю, оскільки об’єм не змінюється. Отже
A p1 V2 V1 . |
(7) |
Зміна внутрішньої енергії знайдена в попередньому пункті. Підставивши чисельні значення величин у Формулу (7), отримаємо
A 1230 Дж, U 600 Дж, Q 1800 Дж.
97
Термодинаміка
Приклад 9.3.3. Двоатомний газ займає об’єм V1=0,5 л при тиску p1=50 кПа. Газ стискається адіабатно до деякого об’єму V2 і тиску p2. Потім він охолоджується при V2=const до початкової температури, причому його тиск стає рівним p0=100 кПа. Накреслити графік процесу. Знайти об’єм V2 і тиск p2.
Розв’язання. Накреслимо графік процесу в координатах pV (рис. 9.3). Ділянка 1- 2 – адіабатний процес, ділянка 2-3 – ізохорний процес. Зазначимо на графіку параметри станів 1, 2, 3.
За умовою в станах 3 і 1 температура однакова, це значить, що вони знаходяться на одній ізотермі. Параметри цих станів пов’язані рівнянням Бойля – Маріотта:
p |
|
|
|
|
|
p1V1 p0V2 . |
(1) |
|||||||
p2 |
|
|
2 |
|
|
Знайдемо об’єм V2: |
|
|
|
|
||||
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
V |
|
p1V1 |
. |
|
(2) |
|||
|
|
|
|
|
|
|
|
|
||||||
p0 |
3 |
|
|
|
|
2 |
|
|
|
p0 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
Процес 1-2 описується рівнянням Пуассона |
|||||||||
p1 |
|
|
|
1 |
|
для адіабатного процесу: |
|
|
||||||
|
|
|
|
p V p V , |
(3) |
|||||||||
|
|
|
|
|
|
|||||||||
0 |
V2 |
V1 |
V |
1 |
|
1 |
|
2 |
2 |
|
||||
де – показник адіабати. |
|
|
||||||||||||
|
Рисунок 9.3 |
|
|
|
|
|||||||||
|
|
|
|
|
C p |
, |
|
|
(4) |
|||||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
Cv |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
де CP i 2 2 R – молярна теплоємність при постійному тиску;
Cv 2i R – молярна теплоємність при постійному об’ємі.
Тоді: |
i 2 R |
|
2 |
|
i 2 |
|
|
||
|
|
|
, |
(5) |
|||||
2 |
|
|
i |
||||||
|
|
iR |
|
|
|
||||
де i – число ступенів свободи, i=5, оскільки газ двоатомний. |
|
||||||||
З рівняння (3) знайдемо тиск p2: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
||||
|
p2 |
|
V1 |
|
|
|
(6) |
||
|
p1 V |
. |
|
||||||
|
|
|
2 |
|
|
|
|
||
Підставивши чисельні значення величин у формули (2), (5), (6), отримаємо:
V 0,25 10 3 |
м3 |
, |
1,4 , |
p |
2 |
1,32 кПа. |
2 |
|
|
|
|
|
Приклад 9.3.4. Ідеальна теплова машина, що працює за циклом Карно, виконує за один цикл роботу А=73,5 кДж. Температура нагрівача t1=100 С, температура
98

Термодинаміка
холодильника t2=0 С. Знайти ккд циклу, кількість тепла Q1, що одержується машиною за один цикл від нагрівача, і кількість тепла Q2, що віддається за один цикл холодильнику.
Розв’язання. Коефіцієнт корисної дії теплової машини
Q1 Q2 , (1)
Q1
де Q1 – кількість тепла, що одержується робочим тілом від тепловіддавача; Q2 – кількість тепла, що віддається робочим тілом теплоприймачу.
Ккд ідеального циклу Карно
T1 T2 , |
(2) |
T1
де T1 и T2 – термодинамічні температури нагрівача і холодильника. Різниця Q1 Q2 дає роботу, що виконується робочим тілом:
Q1 Q2 A .
З урахуванням (3) формулу (1) перепишемо у вигляді:
A .
Q1
Звідси:
Q1 A .
(3)
(4)
(5)
Підставивши чисельні значення величин у формули (2) і (5), отримаємо |
|
0,27 , Q1 272 кДж. |
|
З рівняння (3) знайдемо Q2: |
|
Q2 Q1 A . |
(6) |
Підставивши чисельні значення величин у формулу (6), отримаємо
Q2 198,5 кДж.
Приклад 9.3.5. Теплова машина, робочим тілом якої є ідеальний одноатомний газ, здійснює цикл, зображений на рис. 9.4. Знайти ккд теплової машини.
Розв’язання. Коефіцієнт корисної дії теплової машини визначається співвідношенням:
|
A |
100% , |
(1) |
|
Q |
||||
|
|
|
||
|
1 |
|
|
де А – робота, що виконується за цикл,
99

Термодинаміка
Q1 – кількість тепла, що одержується робочим тілом від тепловіддавача за
цикл.
p |
2 |
|
3 |
Робота циклу дорівнює площі, обмеженій графі- |
||||
2p0 |
|
ками процесу. У нашій задачі – це прямокутний трику- |
||||||
|
|
|
|
|
||||
p |
|
|
|
|
|
тник з основою 4V0 V0 і висотою (2 p0 |
p0 ) . Отже, |
|
1 |
|
|
|
|
|
A 1 3V0 p0 1,5 p0V 0 . |
|
|
0 |
|
|
|
|
|
(2) |
||
|
|
|
|
|
|
|
2 |
|
|
V |
4V V Знайдемо Q1, |
використовуючи перший закон термоди- |
|||||
|
0 |
|
0 |
наміки: |
|
|
||
|
Рисунок 9.4 |
|
|
|
|
|||
|
|
|
Q1 Q12 |
Q23 A12 A23 U , |
(3) |
|||
|
|
|
|
|
|
|||
де |
А12 |
– робота на ділянці 1-2, |
|
|
А23 |
– робота на ділянці 2-3, |
|
|
U – зміна внутрішньої енергії на ділянці 1-2-3. |
|
|
|
|
A12 0, |
(4) |
оскільки процес 1-2 є ізохорний (V=const). |
|
||
|
|
A23 2 p0 (4V0 V0 ) 6 p0V0 , |
(5) |
оскільки процес 2-3 є ізобарний (p=const).
Зміна внутрішньої енергії U на ділянці 1-2-3 буде визначатися початковими і кінцевими значеннями температур, тобто значеннями температур Т1 і Т3 в точках 1 і 3.
U |
i |
|
m |
R T |
T , |
(6) |
|
|
|||||
2 |
|
M |
3 |
1 |
|
|
|
|
|
|
|||
де i – число ступенів свободи. i=3, оскільки газ одноатомний.
Виразимо U через параметри р0 і V0. Для цього запишемо рівняння Менделєєва – Клапейрона для станів 1 і 3:
p V |
|
|
m |
RT |
, |
(7) |
||
|
|
|||||||
0 |
0 |
|
M |
|
1 |
|
||
|
|
|
|
|
|
|
|
|
2 p |
0 |
4V |
m |
RT . |
(8) |
|||
|
||||||||
|
|
0 |
|
M |
3 |
|
||
|
|
|
|
|
|
|
|
|
Віднімемо з рівняння (8) рівняння (7), отримаємо:
7 p V |
|
m |
R(T |
T ) . |
(9) |
|
|
||||||
0 |
0 |
|
M |
3 |
1 |
|
|
|
|
|
|
|
|
Порівнявши (6) і (9), запишемо:
100
