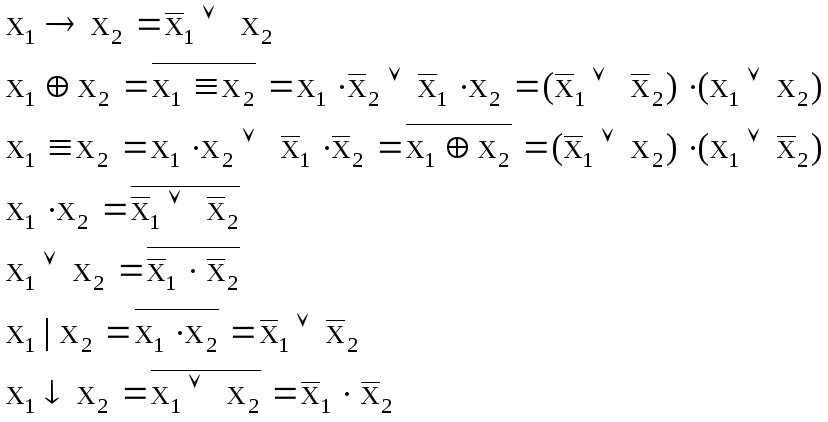- •Методические указания и задания
- •Задание на лабораторную работу
- •Способы задания множеств. Операции над множествами. Основные соотношения алгебры множеств
- •Теоретическая справка
- •Способы задания множеств
- •Операции над множествами
- •Основные законы алгебры множеств:
- •Задание к лабораторной работе.
- •Контрольные вопросы.
- •Отношения на множествах
- •Теоретическая справка
- •Способы задания отношений
- •Свойства бинарных отношений
- •Функциональные отношения
- •Например:
- •Задание к лабораторной работе
- •Основные понятия комбинаторики
- •Правило произведения Теоретико – множественная формулировка правила произведения
- •Комбинаторная формулировка правила произведения
- •Сложный выбор объектов
- •Соединения без повторений
- •Перестановки
- •Размещения из n элементов по m
- •Решение:
- •Сочетания
- •Свойства сочетаний
- •Соединения с повторениями
- •Размещения с повторениями
- •Сочетания с повторениями
- •Формулы пересчета для основных видов комбинаторных соединений
- •Принцип включения- исключения
- •Частные случаи формулы включений и исключений
- •Задача о беспорядках
- •Задача o встречах
- •Перестановки без фиксированных пар
- •Распределения объектов по ячейкам
- •Распределение одинаковых объектов
- •Вместимость ячеек задана
- •Распределение различных объектов по ячейкам с учётом их порядка в различных ячейках Вместимость ячеек неограниченна, ячейки могут быть пустыми
- •Вместимость ячеек неограниченна, ячейки не могут быть пустыми
- •Задания к лабораторной работе
- •Вариант №1.
- •Вариант №2.
- •Вариант №3.
- •Вариант №4.
- •Вариант №5.
- •Вариант №6.
- •Вариант №7.
- •Вариант №8.
- •Вариант №9.
- •Вариант №10.
- •Вариант №11.
- •Вариант №12.
- •Вариант №13.
- •Вариант №14.
- •Вариант №15.
- •Вариант №16.
- •Вариант №17.
- •Вариант №18.
- •Вариант №19.
- •Вариант №20.
- •Вариант №21.
- •Вариант №22.
- •5.Сколькими способами можно переставить буквы в слове «тартар», чтобы одинаковые буквы не шли друг за другом? Вариант №23.
- •Вариант №24.
- •Вариант №25.
- •Вариант №26.
- •Вариант №27.
- •Вариант №28.
- •Вариант №29.
- •Вариант №30.
- •Контрольные вопросы
- •8. Сформулировать общую постановку задачи распределения объектов по ячейкам.
- •Булевы функции. Законы алгебры логики. Аналитические способы описания. Полные системы функций
- •Теоретическая справка Определение функции алгебры логики
- •Табличный способ представления фал
- •Графическое представление фал
- •Функции алгебры логики одного аргумента
- •Функции алгебры логики двух аргументов
- •Элементарные функции алгебры логики
- •Условные приоритеты булевых функций
- •Выражение одних элементарных функций через другие
- •Аналитическая запись фал
- •Дизъюнктивная нормальная форма (днф)
- •Дизъюнктивная совершенная нормальная форма (дснф)
- •Алгоритм перехода от табличного задания функции к дснф
- •Конъюнктивная совершенная нормальная форма
- •Алгоритм построения конъюнктивной совершенной нормальной формы
- •Полные системы фал
- •Задание к лабораторной работе
- •Контрольные вопросы
- •Методы минимизации функций алгебры логики.
- •Теоретическая справка Основные определения
- •Минимизация фал на кубе
- •Метод Квайна минимизации булевых функций
- •Метод Мак-Класки минимизации булевых функций
- •Графический метод минимизации: карты Карно и диаграммы Вейча
- •Основные принципы построения карт Карно
- •Задание к лабораторной работе
- •Алгоритм генерации варианта
- •Контрольные вопросы
Выражение одних элементарных функций через другие
|
|
Аналитическая запись фал
Рассмотрим методы перехода от табличного способа задания функций к аналитическому методу (в виде формул).
Дизъюнктивная нормальная форма (днф)
Элементарная конъюнкция – конъюнкция, в которой каждая переменная встречается не более одного раза.
Дизъюнктивная нормальная форма (ДНФ) – дизъюнкция элементарных конъюнкций.
Например:
Используя законы алгебры логики преобразовать по шагам функцию F(x,y,z) в ДНФ. Для полученного результата составить таблицу истинности.
Решение:
Выполним преобразования по шагам:
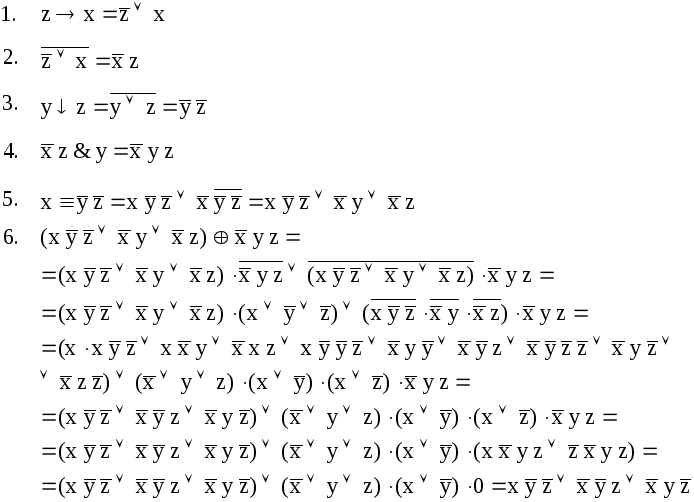
Составим таблицу истинности для полученного результата:
|
x |
y |
z |
|
|
|
|
|
|
|
|
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
|
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
|
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
|
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
|
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
|
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
Последний столбец этой таблицы совпадает со столбцом задания функции F(x,y,z), следовательно, перевод в ДНФ верен.
Дизъюнктивная совершенная нормальная форма (дснф)
Любая таблично заданная ФАЛ f(x1, x2, …, xn) (кроме тождественного нуля) может быть представлена в следующем аналитическом виде:
![]()
Представление ФАЛ в таком виде называется дизъюнктивной совершенной нормальной формойэтой функции (ДСНФ).
Алгоритм перехода от табличного задания функции к дснф
Выбрать в таблице все наборы аргументов, на которых функция обращается в единицу.
Выписать конъюнкции, соответствующие этим наборам аргументов. При этом если аргумент xiвходит в данный набор как 1, он вписывается без изменения в конъюнкцию, соответствующую данному набору. Если xiвходит в данный набор как 0, то в конъюнкцию вписывается его отрицание.
Полученные конъюнкции соединить операцией дизъюнкция.
Конъюнктивная совершенная нормальная форма
Любая таблично заданная ФАЛ f(x1, x2, …, xn) (кроме тождественной единицы) может быть представлена в следующем аналитическом виде:
![]()
Представление ФАЛ в таком виде называется конъюнктивной совершенной нормальной формойэтой функции (КСНФ).
Алгоритм построения конъюнктивной совершенной нормальной формы
Выбрать в таблице все наборы аргументов, на которых функция обращается в 0.
Выписать дизъюнкции, соответствующие этим наборам аргументов. При этом если аргумент xi входит в данный набор как 0, он вписывается без изменения в дизъюнкцию, соответствующую данному набору. Если xiвходит в данный набор как 1, то в дизъюнкцию вписывается его отрицание.
3. Полученные дизъюнкции соединить операцией конъюнкция.
Например:
Построить ДСНФ и КСНФ для функции F(x,y,z).
![]()
Решение:
Для нахождения ДСНФ выбираем из таблицы №4 только те строки, в которых стоят наборы значений аргументов, обращающие функцию в единицу. Это вторая, третья и пятая строки. Выпишем конъюнкции, соответствующие выбранным строкам:
![]() .
.
Соединяя эти конъюнкции знаками дизъюнкции, получаем:
![]() .
.
Для нахождения КСНФ выбираем из таблицы №4 только те строки, в которых стоят наборы значений аргументов, обращающие функцию в ноль. Выпишем соответствующие дизъюнкции и соединим их знаками конъюнкции.
Получим:
![]() .
.