
- •Методические указания и задания
- •Задание на лабораторную работу
- •Способы задания множеств. Операции над множествами. Основные соотношения алгебры множеств
- •Теоретическая справка
- •Способы задания множеств
- •Операции над множествами
- •Основные законы алгебры множеств:
- •Задание к лабораторной работе.
- •Контрольные вопросы.
- •Отношения на множествах
- •Теоретическая справка
- •Способы задания отношений
- •Свойства бинарных отношений
- •Функциональные отношения
- •Например:
- •Задание к лабораторной работе
- •Основные понятия комбинаторики
- •Правило произведения Теоретико – множественная формулировка правила произведения
- •Комбинаторная формулировка правила произведения
- •Сложный выбор объектов
- •Соединения без повторений
- •Перестановки
- •Размещения из n элементов по m
- •Решение:
- •Сочетания
- •Свойства сочетаний
- •Соединения с повторениями
- •Размещения с повторениями
- •Сочетания с повторениями
- •Формулы пересчета для основных видов комбинаторных соединений
- •Принцип включения- исключения
- •Частные случаи формулы включений и исключений
- •Задача о беспорядках
- •Задача o встречах
- •Перестановки без фиксированных пар
- •Распределения объектов по ячейкам
- •Распределение одинаковых объектов
- •Вместимость ячеек задана
- •Распределение различных объектов по ячейкам с учётом их порядка в различных ячейках Вместимость ячеек неограниченна, ячейки могут быть пустыми
- •Вместимость ячеек неограниченна, ячейки не могут быть пустыми
- •Задания к лабораторной работе
- •Вариант №1.
- •Вариант №2.
- •Вариант №3.
- •Вариант №4.
- •Вариант №5.
- •Вариант №6.
- •Вариант №7.
- •Вариант №8.
- •Вариант №9.
- •Вариант №10.
- •Вариант №11.
- •Вариант №12.
- •Вариант №13.
- •Вариант №14.
- •Вариант №15.
- •Вариант №16.
- •Вариант №17.
- •Вариант №18.
- •Вариант №19.
- •Вариант №20.
- •Вариант №21.
- •Вариант №22.
- •5.Сколькими способами можно переставить буквы в слове «тартар», чтобы одинаковые буквы не шли друг за другом? Вариант №23.
- •Вариант №24.
- •Вариант №25.
- •Вариант №26.
- •Вариант №27.
- •Вариант №28.
- •Вариант №29.
- •Вариант №30.
- •Контрольные вопросы
- •8. Сформулировать общую постановку задачи распределения объектов по ячейкам.
- •Булевы функции. Законы алгебры логики. Аналитические способы описания. Полные системы функций
- •Теоретическая справка Определение функции алгебры логики
- •Табличный способ представления фал
- •Графическое представление фал
- •Функции алгебры логики одного аргумента
- •Функции алгебры логики двух аргументов
- •Элементарные функции алгебры логики
- •Условные приоритеты булевых функций
- •Выражение одних элементарных функций через другие
- •Аналитическая запись фал
- •Дизъюнктивная нормальная форма (днф)
- •Дизъюнктивная совершенная нормальная форма (дснф)
- •Алгоритм перехода от табличного задания функции к дснф
- •Конъюнктивная совершенная нормальная форма
- •Алгоритм построения конъюнктивной совершенной нормальной формы
- •Полные системы фал
- •Задание к лабораторной работе
- •Контрольные вопросы
- •Методы минимизации функций алгебры логики.
- •Теоретическая справка Основные определения
- •Минимизация фал на кубе
- •Метод Квайна минимизации булевых функций
- •Метод Мак-Класки минимизации булевых функций
- •Графический метод минимизации: карты Карно и диаграммы Вейча
- •Основные принципы построения карт Карно
- •Задание к лабораторной работе
- •Алгоритм генерации варианта
- •Контрольные вопросы
Способы задания множеств. Операции над множествами. Основные соотношения алгебры множеств
Цель работы: изучение способов задания множеств. Приобретение практических навыков в выполнении операций над множествами и проверке основных соотношений алгебры множеств.
Теоретическая справка
Множество- объединение в одно целое различимых между собой элементов.
Конечное множество- множество, состоящее из конечного числа элементов.
Бесконечное множество- множество, состоящее из бесконечного числа элементов.
Способы задания множеств
1) Перечисление элементов.
Например:
А= {1,3,5,6,889,-10}
2) Задание определяющего свойства.
Например:
X= {x| 1 >х> 5,xє Z};
А= {a2|a- четное число}.
Пустое множество – множество, не содержащее ни одного элемента. Пустое множество обозначается
Универсальное – множество, содержащее все возможные элементы. Универсальное множество обозначается U.
Утверждение "аявляется элементом множестваА" записывается в видеаА (апринадлежитмножествуА).
Утверждение "ане является элементом множестваА" записывается в видеаА (ане принадлежитмножествуА).
Множества А и В называются равными (обозначается А= В), если они состоят из одних и тех же элементов.
Если каждый элемент множества А является также элементом множества В, то говорят, что А содержится или включается в В.
В этом случае пишут А В.
Множество A
называется
подмножеством множества
B, если
![]() .
.
В тех случаях,когда одновременно имеют место соотношения A B и A B, говорят, что A строго включается в B, и используют запись A B.
Операции над множествами
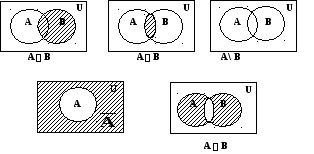
Объединением множеств A и B (обозначается A B) называется множество, состоящее из всех элементов, принадлежащих хотя бы одному из этих множеств, т.е
A B = а а A или аB.
Пересечением множеств A и B (обозначается AB) называется множество, состоящее из всех элементов, принадлежащих каждому из этих множеств, т.е.
АB = а а А иаB.
Разностью множеств А и B (обозначается А\B) называется множество, состоящее из всех элементов множества A , не принадлежащих множеству B, т.е.
А \ B =аа А и аB.
Дополнением множества
А в универсальном
множестве U
(обозначается
![]() ,А)
называется множество, состоящее из всех
элементов универсального множества U,
не принадлежащих множеству А,
т.е.
,А)
называется множество, состоящее из всех
элементов универсального множества U,
не принадлежащих множеству А,
т.е.
А = U \ A
Симметрической разностью множеств A и B (обозначается A B или A B) называется множество, состоящее из всех элементов, принадлежащих в точности одному из этих множеств, т.е.
A B а либо а A и а B, либо а A и а B
A B = (A \ B) (B \ A) = (A B) \ (A B)
Операции над множествами можно проиллюстрировать графически с помощью кругов Эйлера (их также называютдиаграммами Венна). В этом случае исходные множества изображают кругами, а множество-результат выделяют штриховкой.


Основные законы алгебры множеств:
1) Коммутативные законы
АВ=ВА
АВ=ВА
АВ=ВА
2) Ассоциативные законы
А(ВС) = (АВ)С
А(ВС) = (АВ)С
3)Дистрибутивные законы
А(ВС) = (АВ)(АС)
А(ВС) = (АВ)(АС)
4)Законы с иU
А=ААU=АА![]() =U
=U
А=АU=UА![]() =
=
![]() =
=![]() =U
=U
6) Законы идемпотентности
АА=ААА=А ![]() =А
=А
7) Законы поглощения
А(АВ) =АА(![]() В) =АВ
В) =АВ
А(АВ) =АА(![]() В) =АВ
В) =АВ
8) Законы де Моргана
______
AB=![]()
![]()
_______
AB=![]()
![]()
9) Законы склеивания
(АВ)(![]() В) =В
В) =В
(АВ)(![]() В) =В
В) =В
Справедливость законов алгебры множеств доказывается на основе определения равенства: Х=Y, если
1) ХY: xXxY;
2) Y Х: yYyX.
Сформулированный принцип называют интуитивным принципом объемности.
Для доказательств будем использовать следующие обозначения ({- и ;[- или ) и соотношения :
x
A
B
![]() x
A
B
x
A
B
![]()
x
A
B
![]() x
A
B
x
A
B
![]()
x
A \ B
![]() x
A \ B
x
A
x
A \ B
x
A
![]()
![]()
Например:
Используя отношения принадлежности, доказать тождество
(A B) \ C = (A \ C) (B \ C).
Пусть X = (A B) \ C;
Y = (A \ C) (B \ C).
Если x X x (A B) \ C
![]()
![]()
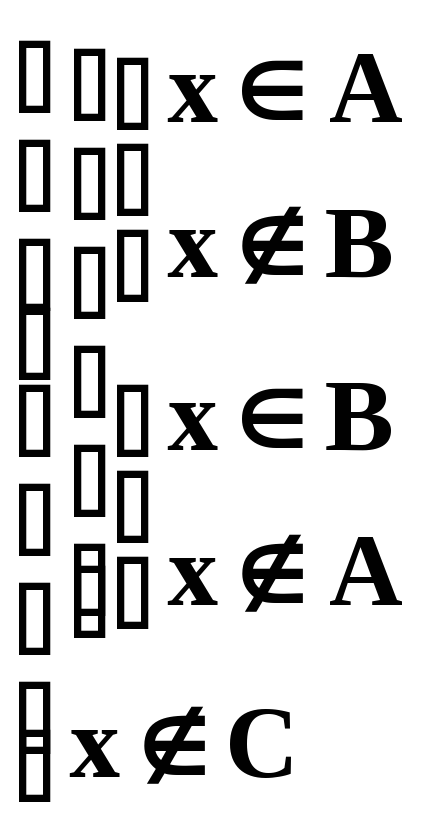

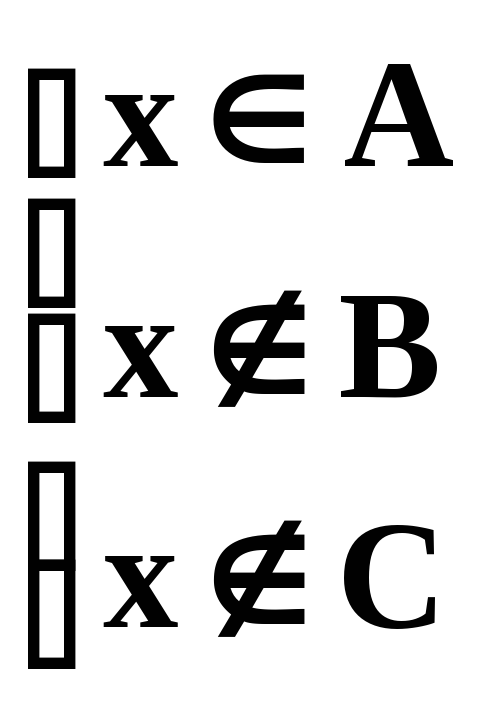 или
или
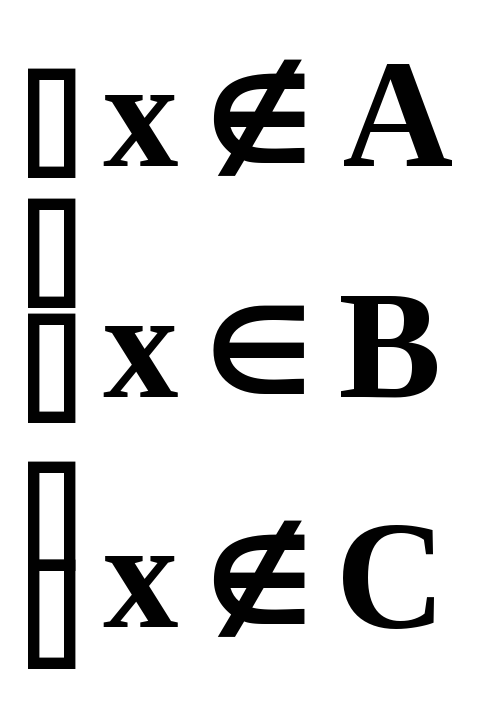 .
.
Если y Y y (A \ C)(B \ C)
y
[(A \
C) \ (B
\ C)]
[(B \ C) \
(A \
C)]
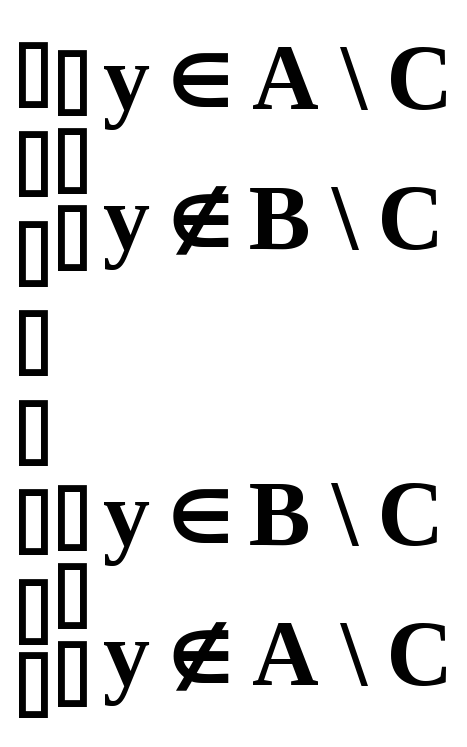
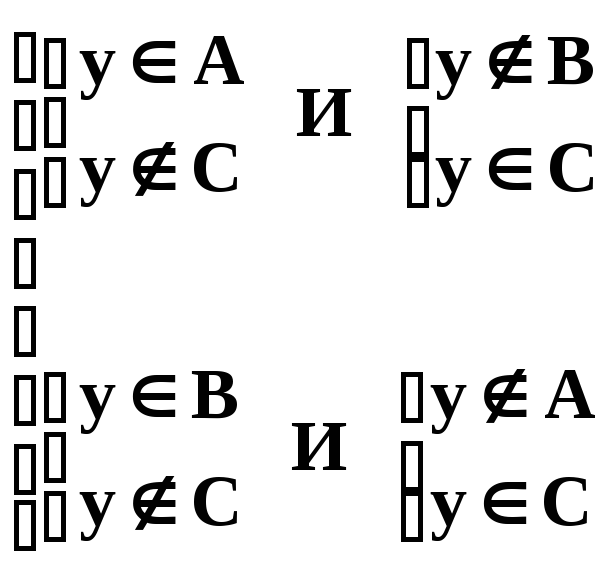
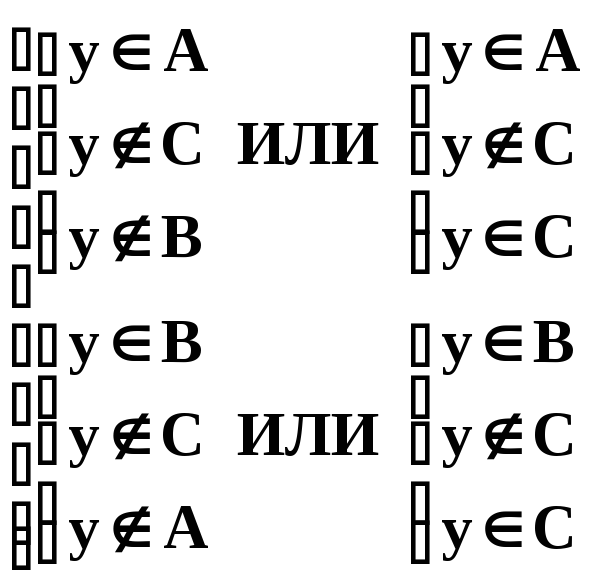

 или
или .
.
Отсюда
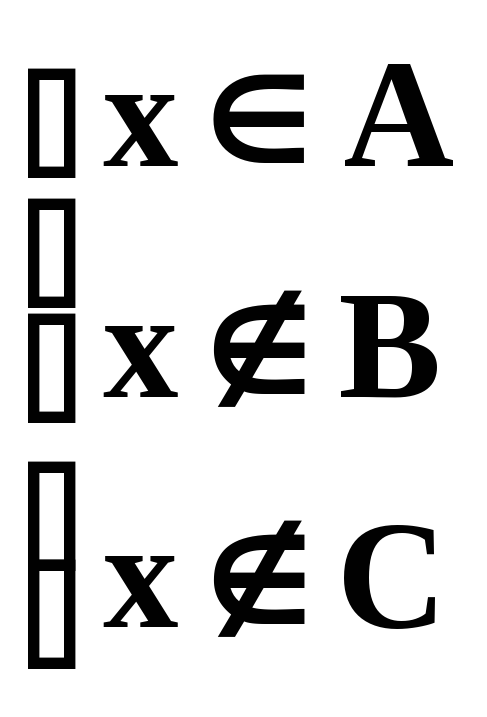 или
или
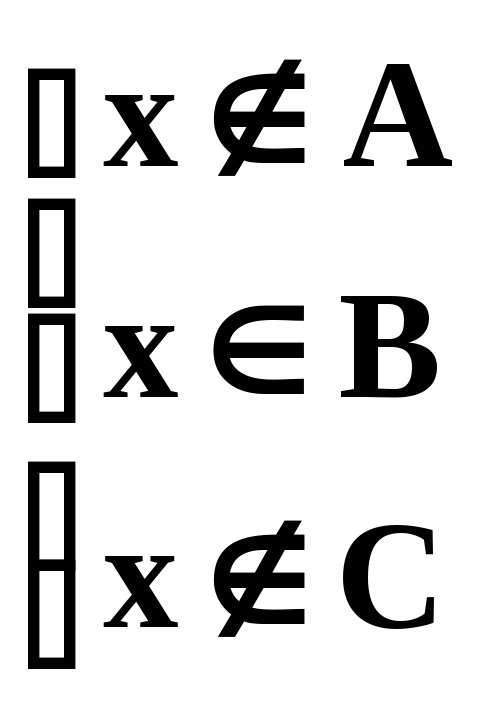 =
=
 или
или
 .
.
Следовательно тождество верно.
