
Физика / Физика / Механика. Лекции / Механика. Пособие
.pdfКогда человек вскочил на тележку, получилась единая система, кото рую тоже можно считать точкой массы (m1 m2 ) .
Ее скорость U и нужно найти.
1)Запишем закон сохранения импульса в проекции на ось X : m1V1 m2V2 (m1 m2 )U1 ,
U1 |
m1V1 m2V2 |
|
60 9 80 3,6 |
5,9 (км/ч). |
|
m1 m2 |
|
140 |
|
2)Запишем закон сохранения импульса в проекции на ось X : m1V1 m2V2 (m1 m2 )U 2 ,
U1 m1V1 m2V2 |
60 9 80 3,6 |
1,8 (км/ч). |
|
|
|
|||||||||
|
|
m1 m2 |
|
140 |
|
|
|
|
|
|
||||
Ответ: U1=5,9 км/ч;U 2=1,8 км/ч. |
|
|
|
|
|
|
|
|||||||
Задача 8. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тележка, |
масса |
которой |
M =120кг, |
движется |
по |
инерции |
по |
|||||||
горизонтальной |
плоскости со скоростью V =6 |
м/с. С тележки соскакивает |
||||||||||||
человек массой |
m =80 кг под углом |
=300 к направлению ее движения в |
||||||||||||
горизонтальной |
плоскости. |
Скорость |
тележки |
уменьшается |
при этом |
до |
||||||||
V =5м/с. Какова была скорость |
U человека во время прыжка относительно |
|||||||||||||
Земли ? |
|
|
|
Решение: |
|
|
|
|
|
|
||||
Дано: |
|
Си: |
|
|
|
|
|
|
|
|||||
M 120кг |
|
|
|
|
|
|
Закон сохранения импульса можно применять |
|||||||
V 6 м/с |
|
|
|
|
только |
для |
составляющих |
импульсов вдоль |
||||||
|
|
|
|
направления движения, так как в этом направлении |
||||||||||
m 80кг |
|
|
|
|
||||||||||
|
|
|
|
внешние силы на систему не действуют: |
|
|||||||||
30 |
|
|
|
|
|
|||||||||
|
|
|
|
(M m)V MV mU cos . |
|
|
|
|||||||
V 5м/с |
|
|
|
|
|
|
|
|||||||
|
|
|
|
Отсюда найдем: |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
||||||
U ? |
|
|
|
|
U |
|
(M m)V MV |
. |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
mcos |
|
|
|
|
||
Вычислим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U |
(120 80) 6 120 5 |
8,6 (м/с). |
|
|
|
|
||||||||
|
80 0,87 |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Ответ: U=8,6 м/с.
Задача 9.
Человек массой m =70 кг находится на корме лодки, находящейся в озере. Длина лодки l=5 м и масса ее M =280 кг. Человек переходит на нос лодки. На
61
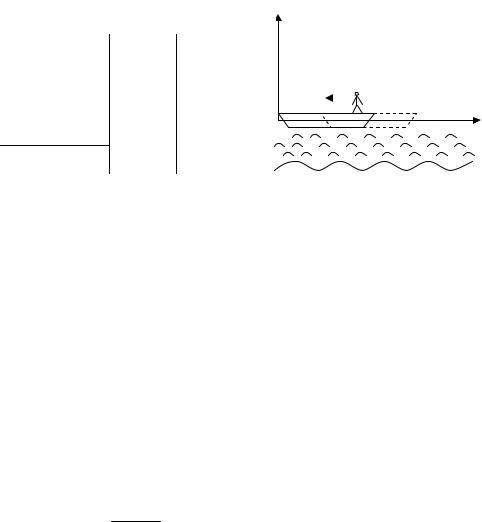
какое расстояние человек передвинется относительно дна? Сопротивлением воды пренебречь.
Y
Дано: Си: m 70 кг
l 5м |
O |
X |
|
M 280 кг |
|||
|
|
||
x -? |
|
|
|
Решение: |
|
Рис. 7 |
|
1-й способ. |
|
|
Количество движения изолированной системы постоянно, а ее центр остается в покое или сохраняет свою скорость неизменной. Поэтому положение центра масс системы "лодка-человек" в системе координат OXY, связанной (рис. 7) с водой, не должно меняться при движении человека:
X цм |
Mа ml |
|
M (a x0 ) mx0 |
, |
|
M m |
M m |
||||
|
|
|
где x0 -координата носа лодки после перемещения человека на нос, m -масса человека,
M -масса лодки,
a -координата центра тяжести лодки.
Отсюда найдем, что лодка переместится на расстояние :
x0 M m m l
относительно дна, а человек на расстояние
x l x0 |
|
M |
l относительно дна. |
|
|
M m |
|||
|
|
|
|
|
Подставим числовые значения: |
||||
280 |
|
|
|
|
x' |
|
5 4 (м). |
||
280 70 |
||||
Ответ: x 4 м.
2-ой способ.
Обозначив через V скорость человека относительно лодки, U -скорость лодки относительно воды, можно записать:
m(V U ) MU ,
62

где (V U ) - скорость человека относительно дна. Откуда
U m V . m M
Учитывая, что пути, проходимые человеком и лодк ой, пропорциональны их скоростям, найдем перемещение лодки x0 относительно дна
x0 |
|
m |
l, |
|||
M m |
||||||
|
|
|
|
|||
а человека |
|
|
|
|
|
|
|
|
|
m |
|
|
|
M m l. |
||||||
x |
||||||
Подставим числовые значения:
x' |
280 |
5 4 (м). |
280 70 |
Ответ: x 4 м.
63
РЕКОМЕНДУЕМОЕ ЗАДАНИЕ
для в н е а у д и т о р н о г о рассмотрения
1.Шарик массой m =100 г, движущийся со скоростью V =1 м/с, упруго ударяется о плоскость. Определить изменение импульса p шарика, если направление скорости составляет с плоскостью угол , равный:
а).900 ; б).300.
|
Отв. а) p = 0,2 Н·с; |
б) p = 0,1Н·с. |
|
|
2. |
Шарик массой m =10 г падает на горизонтальную плоскость с высоты |
|||
|
h =27 см. Найти среднюю силу удара в следующих случаях: а). шарик и |
|||
|
плоскость из стали (абсолютно упругий удар); б). шарик пластилиновый |
|||
|
(абсолютно неупругий удар). |
|
||
|
Рассмотреть эти же случаи удара шарика о плоскость, наклоненную под |
|||
|
углом ( 300 ), |
t 0,03с. |
|
|
|
Отв. а) Fср =1,53 Н; Fср =0,77 H; б) Fср =1,15 H; Fср =0,77 H. |
|||
3. |
Тело массой m =5 кг брошено под углом |
300 к горизонту с |
||
|
начальной скоростью V0 =20 м/с. Пренебрегая сопротивлением воздуха, |
|||
|
найти: 1). импульс силы |
F t , действующей |
на тело, за время его |
|
|
полета; 2). изменение P импульса тела за время полета. |
|||
|
Отв. F t =100 Н·с, P =100 кг·м/с. |
|
||
4. |
Шарик массой |
m =300 |
г ударился о стену |
и отскочил от нее. |
Определить импульс P1,полученный стеной, если в последний момент
перед ударом шарик имел скорость V0 =10 м/с, направленную под углом
300 к поверхности стены. Удар считать абсолютно упругим. Отв. P1 =3 Н·с
5.На железнодорожной платформе установлено орудие. Масса платформы с орудием M=15 т. Орудие стреляет вверх под углом 600 к горизонту
в направлении пути. С какой скоростью покатится платформа вследствие отдачи, если масса снаряда m=20 кг и он вылетает со скоростью V2=600 м/с?
Отв. V1=0,4 м/с.
64
5а. Конькобежец, стоя на льду, бросает груз весом 100 Н под углом 30º к горизонту. Груз падает на расстоянии 2,2 м от точки бросания. Какова будет начальная скорость движения V2 конькобежца, если вес его равен 640 Н. Перемещением конькобежца во время броска пренебречь.
Отв. V2 =0,675 м/с.
6.Снаряд массой m =10 кг обладал скоростью V=200 м/с в верхней точке траектории. В этой точке он разорвался на две части. Меньшая часть
массой m 1 =3 кг получила скорость U1 =400 м/с в прежнем направлении. Найти скорость U2 второй, большей части после разрыва.
Отв. U2 =-114 м/с.
7.В предыдущей задаче найти, с какой ско ростью U 2 и под каким углом2 к горизонту полетит большая часть снаряда, если меньшая полетела
вперед под углом 1 600 к горизонту. Отв. U2 =250 м/с, 2 = 36,60.
8. В лодке массой m1 =240 кг стоит человек массой m2 =60 кг. Лодка плывет со скоростью V1 =2 м/с. Человек прыгает с лодки в горизонтальном направлении со скоростью V=4 м/с (относительно лодки). Найти скорость U движения лодки после прыжка человека в двух случаях: 1). человек прыгает вперед по движению лодки 2). в сторону, противоположную движению лодки.
Отв. U1=1 м/с, U2=3 м/с.
9. Движущееся тело массой m1 ударяется о неподвижное тело массой m2 . Считая удар неупругим, а тела движущимися после удара вместе, найти, какая часть Q первоначальной кинетической энергии K1 переходит при ударе в тепло. Задачу решить сначала в общем виде, а затем рассмотреть случаи: 1). m1 m2 ; 2). m1 9m2 .
Отв. |
Q |
|
|
m2 |
|
; 0,5; 0,1. |
||
K |
1 |
m |
m |
2 |
||||
|
|
|
||||||
|
|
|
1 |
|
|
|||
65
10.Тело массой m1 =2 кг движется по горизонтальной плоскости навстречу телу массой m2 =1,5 кг и неупруго сталкивается с ним так, что после столкновения оба тела двигаются вместе. Скорости тел непосредственно перед столкновением равны:V1 =1 м/с, V2 =2 м/с. Сколько времени t будут двигаться эти тела после столкнов ения, если коэффициент трения k=0,05 ?
Отв. t 0,57 с.
ДОМАШНЕЕ ЗАДАНИЕ
1.Составить конспект ответов на вопросы.
2.Решить следующие задачи:
1.Мяч массой 250г со скоростью 50 м/с ударяется о вертикальную стенку и упруго отскакивает. Стенка получает импульс, равный 2,2 кг ·м/с. Определить угол и силу удара F при продолжительности удара 0,02 с.
Отв. =85˚ , F =110 Н.
2. Под углом 30˚ к нормали стенки подлетает молекула со скоростью 400м/с и массой 3 10 23 г, упруго ударяется и отлетает. Определить импульс силы F t , полученный стенкой.
Отв. F t =2,0·10 23 Н·с
3.Снаряд летит с горизонтальной скоростью 600 м/с и разрывается на два осколка. Один из осколков большей массы падает по вертикали, а другой массой в 2 раза меньше первого, движется после разрыва под углом 30 ˚ к горизонту. Какова скорость V2 второго осколка?
Отв. V2=2,1·103 м/с.
4. Лодка длиной l=3м и массой М=120кг стоит на спокойной воде. На носу
и корме находятся два рыбака массами m1 90 кг и m2 60кг. На сколько сдвинется лодка относительно воды, если рыбаки поменяются местами?
Отв. x |
m1 |
m2 |
l |
0,33м. |
||
m1 |
m2 M |
|||||
|
|
|||||
66
ДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ ТЕЛА, ДВИЖУЩЕГОСЯ ПОСТУПАТЕЛЬНО
Практическое занятие 5
III.Энергия. Работа. Мощность
1.Что такое потенциальная энергия?
2.Рассчитать потенциальную энергию для:
а) тела, поднятого на высоту Н, много меньше радиуса Земли; б) тела, поднятого на высоту Н, сравнимую с радиусом Земли; в) упруго деформированного тела.
3.Сформулировать закон сохранения и превращения механической энергии.
4.Дать понятие элементарной механической работы.
5.Как определяется механическая работа.
а) для постоянной силы? б) для переменной силы?
6.Дать определение кинетической энергии и записать математическое выражение для неё:
а) для тела, движущегося поступательно; б) для вращающегося тела.
7.Сформулировать и записать теорему о кинетической энергии.
8.Какой удар называется абсолютно упругим, абсолютно неупругим.
Какие законы при этом выполняются?
Литература: Т.Гл.3,§11-15,С.23-34,2000.
67
Примеры решения задач
1.Работа движущегося тела
Задача 1.
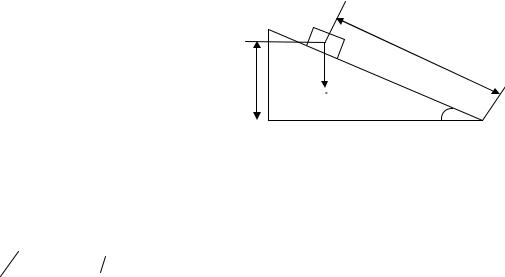
Санки весом 20 Н скатываются с горы, которая образует угол 30 ˚ с горизонтом. Пройдя расстояние 100м, санки развивают скорость 5м/с. Вычислить количество теплоты Q, выделившееся при трении полозьев о снег.
Дано: |
|
Си: |
|
Решение: |
|
|
|
|
|
|
|||
P 20 Н |
|
|
|
Из рис.1 |
видно, что на горе санки |
обл адают |
30 |
|
|
|
потенциальной |
энергией Wп mgh . При |
движении |
S 100 м |
|
|
|
санок с горы |
эта энергия частично п ереходит в |
|
|
|
|
кинетическую, а частично идёт на р аботу против сил |
|||
V 5 м/с |
|
|
|
|||
|
|
|
трения на пути S : |
|
||
|
|
|
|
|
||
Q ? |
|
|
|
Wп Wk Aтр . |
|
|
|
|
|
|
|
|
|
Внашем случае энергия, идущая на преодоление сил трения, выделяется
ввиде тепла:
Q Aтр ; |
Wп Wk Q ; |
. |
S |
|
||||||||
|
|
|
|
|
||||||||
Q Wп Wk ; |
Q mgh |
mV 2 |
h |
|
|
|||||||
|
|
|
||||||||||
|
|
|
|
|
2 |
|
|
P |
|
|
||
Так, как h S Sin ,то |
|
|
|
|
|
30 |
o |
|||||
|
|
|
|
|
|
|
||||||
Q m 2gS sin V 2 |
|
|
|
|
|
Рис. 1 |
|
|
||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
В системе СИ: m |
P |
|
20 |
2,0 (кг); |
|
|
||||||
|
9,8 |
|
|
|||||||||
|
|
|
g |
|
|
|
|
|
|
|
||
Подставляя данные задачи: |
|
|
|
|
|
|
|
|
||||
Q 1 |
2 |
2 10 100 1 2 25 487,5 |
(Дж). |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: Q=487,5 Дж. |
|
|
|
|
|
|
|
|
|
|
||
Задача 2.
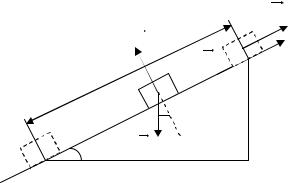
Какую работу совершит сила тяги F 30Н , подняв по наклонной плоскости груз массой m 2кг на высоту h 2,5м с ускорением a 5 м/с . Сила действует параллельно наклонной плоскости. Трением о плоскость пренебречь.
68
Дано: |
|
Си: |
|
Решение: |
|
|
|
|
|
|
|
||||
F 30 Н |
|
|
|
Работа силы F равна изменению полной |
|||
m 2 кг |
|
|
|
механической энергии груза: |
|
||
|
|
|
А К1 |
П1 К0 П0 , |
(1) |
||
h 2,5 м |
|
|
|
||||
a 5 м/с |
|
|
|
где К0 и |
П0 , К1 |
и П1 - соответственно кинетическая и |
|
|
|
|
|
|
|
началь ном (О) и |
|
|
|
|
|
потенциальная |
энергии груза в |
||
А ? |
|
|
|
||||
|
|
|
|
|
О |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
конечном ( 1) состояниях (рис.2). |
|
||
Будем отсчитывать потенциальную э нергию плоскости. Тогда:
П0 0, П1 |
mgh , |
|
|
|
К0=0, К1 |
mV |
2 |
|
|
1 |
, |
|
|
|
|
2 |
|
|
|
где V1 -скорость груза в точке O1. |
|
|
||
Квадрат этой скорости найдём из |
|
|
||
кинематического соотношения: |
|
|
||
V12 V22 2аl . |
. |
|
||
Так как V0 0 , то V12 2al , |
O |
|
||
от основания
N
l F
.
P
Рис. 2
где l – длина наклонной плоскости. Учитывая это, в ыражение записать в виде:
наклонной
V1
. X
O1
h
(1) можно
A mal mgh . |
|
|
(2) |
||||
Как видно из рис. 2 |
l |
h |
. |
||||
sin |
|||||||
|
|
|
|
|
|
||
Подставив это значение в (2), получим: |
|||||||
a |
|
|
|
|
|
||
A mh |
|
|
g . |
|
(3) |
||
|
|
|
|||||
sin |
|
|
|
|
|||
Чтобы найти sin , составим уравнение движения груза вдоль оси ОХ:
F mg sin ma .
Отсюда:
sin F ma . mg
Подставляя это значение в формулу (3), получим
A |
Fmgh |
|
30 2 |
9,8 2,5 |
73,5(Дж). |
|
F ma |
30 |
2 5 |
||||
|
|
|
Ответ: A=73.5 Дж.
69
Задача 3.
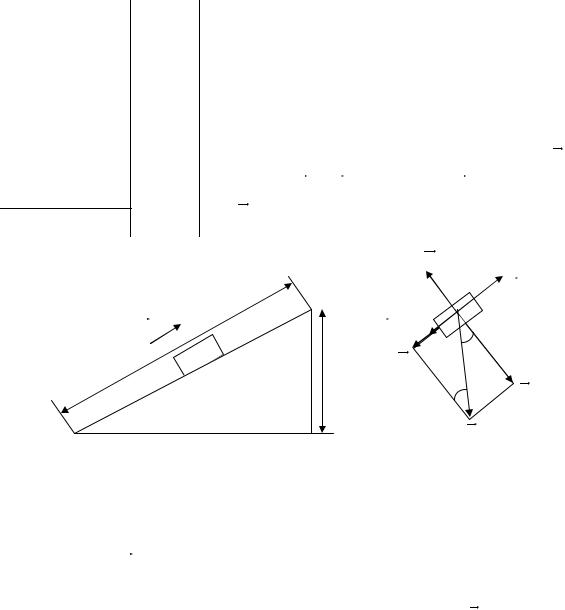
Вагонетку массой m =3т поднимают по рельсам в гору, наклон которой к горизонту равен =30˚ . Какую работу совершила сила тяги на пути S =50м, если известно, что вагонетка двигалась с ускорением а =0,2 м/с ? Коэффициент трения принять равным f 0,1 ; g 10 м/с .
Дано: Си:
m 3т |
3 103 кг |
30 |
|
S 50 м |
|
а 0 , 2 |
м/с |
f= 0,1
g10 м/с
А?
a.
S
Решение:
По условию задачи необходимо вычислить работу постоянной силы тяги F . Эта работа определяется соотношением:
(1)
Делаем чертёж (рис. 3) и расставляем силы, действующие на вагонетку: это сила т яги F , сила тяжести P mg , сила трения F тр и реакция опоры
N .
|
|
|
N |
|
|
|
|
. |
F тр |
|
|
|
|
|
|
|
|
|
|
m |
P sin |
|
||
|
||||
|
|
h |
F |
|
|
|
|
||
|
|
|
|
P cos |
|
|
|
|
|
P
Рис. 3
По условию задачи сила тяги направлена вдоль перемещения, поэтому
угол между F и перемещением равен нулю и, следовательно, |
cos 1 (этот |
|||
угол не следует путать с углом наклона плоскости). |
|
|||
Для определения силы тяги |
разложим силу тяжести P , как обычно, на |
|||
составляющие Psin |
и |
Pcos |
и запишем уравнение второго закона |
|
динамики в проекциях на ось, совпадающую с ускорением а: |
|
|||
F P sin Fmp ma . |
|
|
||
Откуда с учётом того, что |
|
|
||
Fmp fN fP cos |
и P mg , получим: |
|
||
70
