
Физика / Физика / Механика. Лекции / Механика. Пособие
.pdf
Си: Решение: |
|
|
|
|
|
|
1 случай: |
|
|
|
|
|
|
Из |
определения |
средней |
||||
имеем V |
пут |
|
s1 |
s2 |
(1), |
где s и |
|
|
|||||
|
|
t1 |
t2 |
1 |
||
|
|
|
|
|||
путевой скорости
s2 пути, пройденные
автомобилем за все время движения t t1 t2 . Путь в задаче не дан, но мы знаем скорость на обеих его половинах. Через них и выразим путь и время.
t |
|
s1 |
; |
t |
2 |
|
|
s2 |
, но s s |
2 |
|
s |
. |
|
||||||||||||||
|
|
|||||||||||||||||||||||||||
1 |
V1 |
|
|
V2 |
|
|
1 |
|
|
2 |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Подставляя в (1), имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
s |
|
s |
|
|
|
|
2V1V2 |
|
|
|
|
2 80 40 |
|
|||||||
V пут |
|
|
2 |
2 |
|
|
|
|
|
|
54 (км/ч) |
|||||||||||||||||
|
|
s |
|
|
|
|
|
|
|
|
|
80 40 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
s |
|
V1 V2 |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
2V |
|
|
2V |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Ответ: 54 км/ч. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Дано: |
|
Си: |
|
|
2 случай: |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
t1 = ½ t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Предположим, что общее время движения t |
||||||||||||
t2 = ½ t |
|
|
|
|
|
|
|
известно. По определению |
||||||||||||||||||||
V1 = 80 км/ч |
|
|
|
|
|
|
|
V пут |
|
s1 s2 |
|
|
|
|
||||||||||||||
V2 = 40 км/ч |
|
|
|
|
|
|
|
|
t |
|
|
|
|
; |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
<V>пут - ? |
|
|
|
|
|
|
|
Выразим |
|
s |
и |
|
s |
2 |
- пути, пройденные за первую и вторую |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|||
половину времени через t .
s1 V21t и s2 V22t .
Найдем численное значение средней путевой скорости:
|
V |
t |
V |
|
t |
|
|
|
|
|
|
|
|
2 2 |
|
V1 V2 |
|
80 |
40 |
|
|||
V пут |
1 2 |
|
|
|
60 (км/ч) |
||||||
|
t |
|
|
2 |
|
||||||
|
|
|
2 |
|
|
|
|||||
Ответ: 60 км/ч.
Вывод: средняя путевая скорость движения не является средней арифметической от скоростей на разных участках пути.
Задача 5.
Моторист направляет движение лодки так, что если бы не было течения реки, лодка двигалась бы перпендик улярно к берегу со скоростью
V0 7,2 км/ч. Течение относит лодку на l =150 м вниз по реке. Найти скорость
11
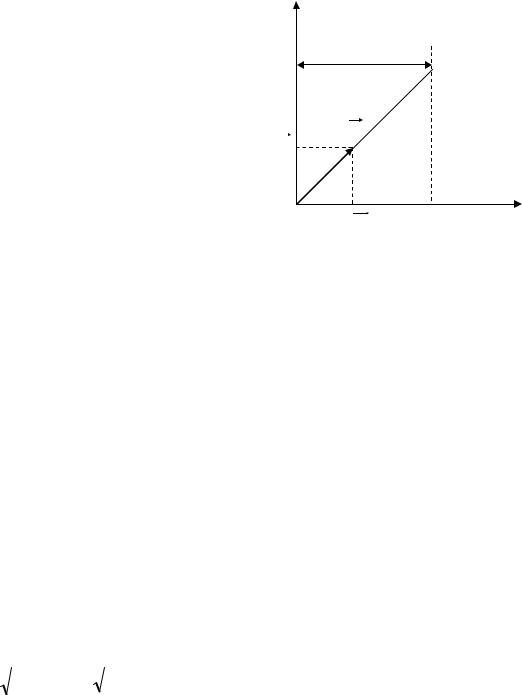
течения реки Vp , время tn , затраченное на переезд через реку, скорость
движения лодки Vл . Ширина реки h 0,5 км. |
|
|
|
|
|
||||||||
Дано: |
|
|
|
Си: |
|
|
Решение: |
|
|
|
берега Vл |
||
V0 7,2 км/ч |
|
|
12 м/с |
|
|
Скорость лодки |
относительно |
||||||
l =150 м |
|
|
|
|
|
|
(искомая) направлена из т.О в т.В (см. рис.4). |
||||||
|
|
500 м |
|
|
|
|
|
y |
|
|
|
||
h 0,5 км |
|
|
|
|
Скорость |
V0 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||
Vp - ? |
|
|
|
|
|
|
задана: |
она |
A |
l |
B |
||
tn - ? |
|
|
|
|
|
|
направлена |
по |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
ОА |
и |
ее |
|
|
|
|
|
Vл -? |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
численное |
|
|
|
|
|
||
|
|
|
|
|
|
|
значение |
|
V0 |
V |
h |
||
известно. Скорость Vp |
|
x |
|||||||||||
направлена вдоль оси |
|
|
|
||||||||||
(вдоль берега). Скорости V0 и Vp являются |
|
|
|
|
|||||||||
проекциями вектора |
V на оси y и |
x |
0 |
Vp |
|
x |
|||||||
соответственно. |
|
Запишем закон |
движения |
|
|
Рис. 4 |
|||||||
лодки, поскольку составляющие |
скоростей |
|
|
|
|||||||||
|
|
|
|
||||||||||
постоянны: |
|
и Vy V0 |
|
|
|
|
|
|
|||||
Vx Vp |
|
|
|
|
|
|
|
||||||
Если |
|
|
|
|
|
|
|
|
|
|
|
|
|
dx V |
p |
и dy |
V , то |
|
|
|
|
|
|
||||
dt |
dt |
0 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|||
x Vpt
yV0t .
Взакон движения подставим координаты т. В, в которую лодка попадает при t tn .
При t tn |
координаты xВ l 150 м, |
y В |
|
h 500 м. Поэтому из |
Vp |
|
x |
|||||||||||
V 0 |
y |
|||||||||||||||||
получаем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
300 |
|
|
|
|
|
|
|
|
||||
Vp |
|
150 ; |
Vp |
0,6 (м/с) |
|
|
|
|
|
|
||||||||
|
2 |
|
|
|
|
|
|
|||||||||||
|
|
500 |
|
500 |
|
|
|
|
|
|
|
|
||||||
tn |
|
yВ |
|
500 |
250 |
(с) |
|
|
|
|
|
|
||||||
|
|
2 |
|
|
|
|
|
|
||||||||||
|
|
|
V0 |
|
|
|
|
|
|
|
|
|
|
|||||
Vл |
|
|
|
|
|
|
12,0 (м/с). |
|
|
|
||||||||
V02 |
Vp2 |
|
122 0,62 |
|
|
|
|
|||||||||||
Ответ: Vp =0,6м/с; |
tn =250с; Vл =12,0м/с. |
|
|
|
|
|
||||||||||||
12

Задача 6.
При равноускоренном движении из состояния покоя тело проходит за
пятую секунду 90 см. Определить перемещение тело за cедьмую секунду. |
|
|||||||||||
Дано: |
|
|
Си: |
|
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
S5 90 см |
|
|
0,9м |
|
Проведем |
ось |
0 |
|
|
x |
||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
x в направлении |
. |
|
|
|
||
S7 - ? |
|
|
|
|
|
|
x4 |
|
|
S5 |
||
|
|
|
|
|
движения тела, |
а |
|
|
|
|||
|
|
|
|
|
|
|||||||
начало оси выберем в точке 0, из которой тело |
|
x5 |
|
|||||||||
|
|
|||||||||||
начинает движение (рис.5). Тогда, согласно |
|
|
|
|
Рис. 5 |
|||||||
уравнению движения координаты тела: |
|
|
|
|
|
|
||||||
x |
4 |
at42 |
; |
x at52 , |
|
|
|
|
|
|
||
|
2 |
|
5 |
2 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|||
где t4 4с, |
|
t 5 |
5 |
с. |
|
|
|
|
|
|
|
|
Следовательно, перемещение тела за пятую секунду |
|
|||||||||||
S5 x5 x4 a2 (t52 t42 ),
откуда
a |
2S5 |
. |
(1) |
|
t52 t42 |
||||
|
|
|
Аналогично, перемещение тела за седьмую секунду:
S7 x7 x6 a2 (t72 t62 ) ,
где . t6 6с, t7 7 с.
С учетом уравнения (1), получим:
S |
7 |
|
S5 (t72 t62 ) |
S5 (t7 t6 )(t7 t6 ) |
; |
|
|
||||||
|
|
t52 t42 |
|
(t5 t4 )(t5 t4 ) |
|
|
Подставим численные значения: |
|
|||||
|
|
|
S7 |
0,9(7 6)(7 6) 1,3 |
(м). |
|
|
|
|
|
|
(5 4)(5 4) |
|
Ответ: S7 1,3 м
Задача 7.
Мяч, брошенный вертикально вверх, упал на землю через 3с. С какой скоростью был брошен мяч, и на какую высоту он поднимался?
13

|
Дано: |
|
Си: |
|
|
|
Направим ось y |
вертикально вверх, начало оси |
||||||||
|
|
|
|
|
||||||||||||
t1 |
3 с |
|
|
|
|
|
выберем на поверхности земли (рис.6). Тогда |
|||||||||
|
|
|
|
|
|
|
уравнение |
|
движения |
тела и формула скорости |
||||||
V0 |
-? |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
примут вид: |
|
|
|
|
|
||||||
yмax -? |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
y V t |
gt |
2 |
, |
|
(1) |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
0 |
|
2 |
|
|
|
|
|
|
|
|
V V0 gt , |
|
|
(2) |
|
|
|
|
||||||||
|
|
|
|
|
Y |
|||||||||||
На поверхности земли t |
t1 , y 0, следовательно |
|
||||||||||||||
|
|
. |
A |
|||||||||||||
уравнение (1) можно привести к виду: |
|
|
|
|||||||||||||
|
|
|
|
|||||||||||||
|
0 V0t1 |
gt2 |
|
|
|
|
|
|
|
|
|
|
||||
|
|
1 |
. |
|
|
|
|
|
|
g |
||||||
|
|
2 |
|
|
|
|
|
|
||||||||
Откуда |
|
|
|
|
|
|
|
|
|
|
|
|
|
V0 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
V gt1 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
0 |
2 |
|
|
|
|
|
|
|
|
|
|
0 . |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
V0 |
9,8 3 |
14,7 |
м/с. |
|
|
|
|
|
|
|
Рис. 6 |
||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В наивысшей точке А подъема мяча |
t tмax , y yмax , V 0. |
|
|
|
|
|||||||||||
Уравнение (2), записанное для точки А, дает |
|
|
|
|
|
|||||||||||
0 V0 gtмax ,
откуда время подъема до точки А:
tмax |
V0 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
g |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Подставляя |
в |
уравнение |
(1) |
полученное |
значение |
tмax , |
||||||||||||
высоту подъема мяча: |
|
|
|
|
|
|
|
|
|
|
|
|||||||
yмax V0tмax |
gtмax2 |
|
V0 |
V0 |
|
gV02 |
V02 |
; |
|
|
||||||||
|
|
g |
|
|||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
2g 2 |
|
2g |
|
|
|
|||
yмax |
14,7 |
11 |
(м). |
|
|
|
|
|
|
|
|
|
||||||
|
2 9,8 |
|
|
|
V |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Ответ:V0 14,7 м/с, |
|
yмax |
|
11м |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
||||||||||
Задача 8. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
Как |
|
|
|
|
|
|
двигался |
|
|
|
|
|
||||||
|
|
|
|
|
|
0 . |
1 |
|
||||||||||
мотоциклист, |
график скорости |
|
|
|
C |
|||||||||||||
|
|
|
|
|
||||||||||||||
движения |
которого |
|
изображен |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
||||||||||||
на рис. 7? |
Рис. 7 |
|
найдем наибольшую
D K
E F
14

Ответ: Из графика видно, что мотоциклист начал свое движение из состояния покоя (точка О). На участке ОА он двигался равноускоренно, на участке АВ его движение было равномерным, а на участке ВС - равнозамедленным с большим по абсолютной величине ускорением, чем на участке ОА ( tg 1 tg 2 ).
Участок СD соответствует остановке. Участки графика DЕ, EF, FK соответствуют движению мотоциклиста в обратном направлении: равноускоренному (участок DЕ), равномерному (участок EF) и равнозамедленному (участок FK).
В предыдущих задачах 1, 2, 4 - 7 мы научились решать прямую основную задачу кинематики: находить любой параметр движения по известному закону движения (путем последовательного применения основ ных законов кинематики). Обратная задача кинематики состоит в определении закона движения по какомулибо известному параметру движения (вектора
скорости V или ускорения a ). Обратная задача значительно труднее п рямой. Рассмотрим пример обратной задачи кинематики.
Задача 9.
Зависимость скорости тела от времени задана уравнением V 0,3t2 (м/с).
Определить путь, пройденный телом за промежуток времени от |
t1 2 с до |
||||||
t2 5 |
с. |
|
|
|
|
|
|
Дано: |
Си: |
Решение: |
|
|
|
|
|
V 0,3t2 (м/с) |
|
Перед нами обратная задача кинематики: дан |
|||||
t1 2 |
с |
|
какойто |
параметр |
движения (в |
данном случае |
|
|
скорость |
V ), надо |
определить |
закон |
движения |
||
t2 5 |
|
|
|||||
с |
|
s f t и найти путь, пройденный за время от t1 до |
|||||
|
|
|
t2 . |
|
|
|
|
S ? |
|
|
|
|
|
|
|
Так как движение тела одномерно (вдоль оси ОХ), то для нахождения закона его движения имеем одно дифференциальное уравнение
dS Vdt или ds 0,3t2dt .
15

После интегрирования имеем:
t2 |
t2 |
2 |
t2 |
2 |
|
t3 |
|
5 |
|
53 |
|
23 |
s ds Vdt 0,3t |
dt 0,3 t |
dt 0,3 |
|
0,3( |
|
|||||||
|
|
3 |
|
2 |
3 |
3 ) 11,7 (м). |
||||||
|
|
|
|
|
|
|||||||
t1 |
t1 |
|
t1 |
|
|
|
|
|
|
|
|
|
Ответ: S 11,7 м.
РЕКОМЕНДУЕМОЕ ЗАДАНИЕ
для в н е а у д и т о р н о г о рассмотрения
1. Прямолинейное |
движение |
точки |
описываетс я |
уравнением |
s 4t4 2t2 7 . |
Найти скорость |
V и |
ускорение точек |
a в момент |
времени t 2с и среднюю скорость V за первые 2 с движения. Отв. V 136м/с, a 196м/с 2 ,V 36м/с.
2. Материальная точка движется прямолинейно с начальной скоростью
V0 10 м/с и |
|
постоянным ускорением |
a 5м/с 2 . |
Определить, во |
||
сколько раз |
путь s , пройденный |
материальной |
точкой, |
будет |
||
превышать модуль ее перемещения r спустя |
t 4 с после |
начала |
||||
отсчета времени. |
|
|
|
|
||
Отв. S |
r |
20/0. |
|
|
|
|
|
|
|
|
|
|
|
3.Камень, брошенный вертикально вверх, упал на землю через 2с. Определить путь и перемещение камня за 1; 1,5; 2с. Какую скорость приобретет камень за эти промежутки времени? Чему равна средняя скорость перемещения камня за все время движения?
Отв. S1 4,9м ; r 6,12м; S3 9,8м ; 4,9м; 3,7м; 0;0; 4,9 м/с; 9,8м/с; 0.
4. Велосипедист ехал из одного пункта в другой. Первую треть пути он
проехал со скоростью V1 18 км/ч. |
Далее половину оставшегося |
времени он ехал со скоростью V2 22 |
км/ч, после чего до конечного |
пункта он шел пешком со скоростью V 3 |
5 км/ч. Определить среднюю |
путевую скорость V велосипедиста. |
|
Отв. V =14,7 км/ч. |
|
16
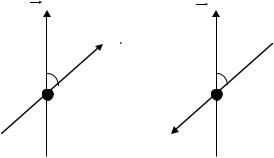
5. Две автомашины движутся по дорогам, угол между которыми 600 . Скорость автомашин V1 54 км/ч и V2 72 км/ч. С какой скоростью
Vудаляются машины одна от другой в случаях:
1)рис. 8а?
2)рис. 8б?
Отв. 1) V 18,03 м/с, 2) V 30,41 м/с.
V1 |
|
|
|
V |
|
|
1 |
||
|
V2 |
|
|
|
|
|
|
|
|
|
перекресток |
|
|
перекресток |
|
|
|
|
2 |
|
|
V |
||
а) |
Рис. 8 |
|
|
б) |
|
|
|
|
|
6. Движение точки по прямой задано уравнением x at bt2 , где a 2м/с; b -0,5 м/с 2 . Определить среднюю путевую скорость V точки в
интервале времени от t1 1с до t2 3с. Отв. V = 0,5м/с.
7. Тело массой m 0,5 кг движется прямолинейно, причем зависимость пройденного телом пути S от времен t выражается уравнением s a bt ct2 dt3 , где с=5м/с 2 , d=1м/с 3 . Найти силу F , действующую на тело в конце первой секунды движения.
Отв. F =2H.
8. Уравнение скорости имеет вид: V 2 ; |
V 20 6t ; |
V 2 3t ; |
V 0,3 4t ; V t . Запишите уравнение перемещения и постройте графики зависимости скорости и перемещения от времени.
9. Рядом с поездом на одной линии с передними буфе рами паровоза стоит
человек. В тот момент, |
когда поезд начал |
двигаться с |
ускорением |
a 0,1 м/с , человек начал идти в том же направлении |
со средней |
||
скоростью V=1,5м/с. Через какое время t |
поезд догонит человека? |
||
Определите скорость V1 |
поезда в этот момент и путь S, пройденный за |
||
это время человеком. |
|
|
|
17
Отв. t 30с; V1 3м/с; S 45м.
10.Точка движется прямолинейно со скоростью, зависимость которой от времени выражается уравнением V 2,5t2 10t . Определите путь S, пройденный точкой за 5с движения.
Отв. S=229,2 м.
ДОМАШНЕЕ ЗАДАНИЕ
1.Составить конспект ответов на вопросы.
2.Решить следующие задачи:
1. Тело прошло первую половину пути за время t1 2 с, вторую за время t2 8 с. Определить среднюю путевую скорость V
пути s 20 м
Отв. V = 2м/с.
2. Движение |
материальной |
точки задано уравнением |
x at bt2 , где |
a 4 м/с, |
b 0,05 м/с 2 . |
Определите момент времени |
t, в который |
скорость V точки равна нулю. Найти координату x и ускорение a в этот
момент. Построить графики зависимости |
координаты x(t), пути S(t), |
|||||||||||||
скорости V(t) и ускорения a(t) этого движения от времени. |
||||||||||||||
|
Отв. t=40с; x=80м; a= 0,1м / с2 ; (графики изображены на рис.9). |
|||||||||||||
|
|
V, м/с |
|
|
|
|
|
|
|
|
||||
X,S,t |
Путь |
4 |
|
|
|
|
|
|
|
|
|
|
t, с |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
40 |
80 |
|
||||||
80 |
|
a, м/с2 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Координата |
0 |
|
|
|
|
|
|
|
|
|
|
t, с |
|
|
|
|
|
|
|
|
|
|
||||||
|
-0,1 |
|
|
|
|
40 |
80 |
|
|
|||||
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t, с
40 80
Рис. 9 (ответ к дом. задаче №2)
18
3. |
Тело брошено с балкона вертикально вверх |
со скоростью V0 10 м/с. |
|
Высота балкона над поверхностью земли h 12,5 м. Написать уравнение |
|
|
движения и определить среднюю путевую скорость V с момента |
|
|
бросания до момента падения на землю. |
|
|
Отв. V = 7,79 м/с. |
|
4. |
Поезд движется прямолинейно со скоростью |
V0 180 км/ч. Внезапно на |
|
пути возникает препятствие, и машинист включает тормозной механизм. |
|
|
С этого момента скорость поезда изменяе тся по закону V V0 t 2 , где |
|
1 м/с 3 . Каков тормозной путь S поезда? Через какое время t после начала торможения он остановится?
Отв. S 235,7 м, t 7 с.
19
КИНЕМАТИКА
Практическое занятие 2
II.Криволинейное движение
1.В каких двух движениях участвует тело, броше нное под углом к горизонту в безвоздушном пространстве?
2.Что характеризует тангенциальная составляющая ускорения и как она определяется?
3.Что характеризует нормальная составляющая ускорения и как она определяется?
4.Как направлены тангенциальная и нормальная составляющие ускорения к траектории движения?
5.Как найти полное ускорение при криволинейном движении?
Литература: Т., Гл.1,§ 3, стр.9, 2000.
Примеры решения задач
Задача 1.
Тяжелое тело брошено вверх с высоты 12 м под углом 30 º к горизонту с начальной скоростью 12 м/с. Определить продолжительность полёта тела до точки A и до точки B (рис.1), максимальную высоту, которую достигает тело , дальность полёта тела. Сопротивлением воздуха пренебречь.
20
