Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Ухтинский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Механика. Пособие

.pdf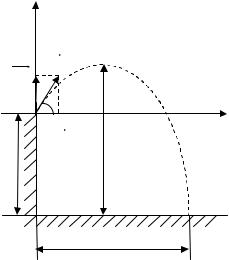

Скачиваний:

139

Добавлен:

02.03.2016

Размер:

859.12 Кб

Скачать

☆

<<< < Предыдущая 1 23 / 143 4 5 6 7 8 9 10 11 12 13 14 > Следующая >>>

Дано:

Си:

Решение:

H 12 м

Сделаем

чертеж

(рис.1).

Прямоугольную

300

систему координат выбираем так, чтобы её начало

V0 12 м/с

совпало с точкой бросания, а оси был и направлены

вдоль поверхности земли

и по нормали к ней в

tA ,tB ,Ymax , X max -?

сторону

начального

смещения

тела. Изображаем

траекторию тела,

его

начальную скорость, угол

бросания φ, высоту Н, горизонтальное перемещение

X max .

Движение тела, брошенного под углом к горизонту, можно представить

как результат сложения

двух прямолинейных

движений: одного вдоль поверхности Земли

(оно

будет

равномерным,

поскольку

сопротивление

воздуха

не

учитывается)

второго

–

перпендикулярно поверхности

Voy

Земли (в данном случае это будет движение

тела, брошенного вертикально вверх).

Vox

Для замены сложного движения двумя

Ymax

простыми

разложим

(по

правилу

параллелограмма) скорость на горизонтальную

и вертикальную составляющие и

найдём её

X max

проекции:

Vox

VoСos ,

Рис. 1.

Voy

Vo Sin .

Составляем уравнения

скорости

перемещения

для проекций по

каждому направлению.

Т.к. в горизонтальном направлении тело летит равномерно, то его

скорость и координаты в любой момент времени удовлетворяют уравнениям:

Vox

VoСos

(1)

X Vox t VotCos .

(2)

Для вертикального направления:

Voy gt Vo Sin gt

(3)

Y H V tSin

gt 2

(4)

Время подъёма тела найдём из условия, что в наивысшей точке подъема тела скорость Vy 0 .

Тогда из уравнения (3)

tподъема

Vo Sin

(5)

Время спуска тела от т. С до т. А

равно времени подъёма, поэтому

продолжительность полёта тела от т. О до т. А равна:

tA 2tподъема

2Vo Sin

(6)

Максимальную высоту подъёма найдём из уравнения (4), подставив

в него время подъёма из уравнения (5):

2 Sin

(7)

max

Время

полёта

тела до

т. В

найдём из уравн ения (4), приравняв

координату Y к нулю (Y =0):

tB Vo Sin

Vo Sin 2

(8)

g 2

Дальность полёта найдём из уравнения (2), подставив в не го время

движения из уравнения (8):

X max VotВCos .

(9)

Произведем вычисления по формуле (6):

t A

2Vo Sin

2 12 0,5

1,22

(с),

9,81

по формуле (8):

12 0,5

2 12

2,29 (с),

9,81

по формуле (7):

12 122

0,52

12 1,84 13,84 (м),

max

2 9,81

по формуле (9):

X max 12 0,867 2,29 23,8 (м).

Ответ: tA 1,22 с,

2,29 с,

Ymax 13,84 м,

X max 23,8 м.

Задача 2.

По условию задачи 1 найти в момент приземления тела следующие величины: скорость и угол падения тела, тангенциальное и нормальное ускорения тела и радиус кривизны траектории.

Дано: Си: Решение:

	H 12 м	1) Результирующая или мгновенная скорость
	300	в т.В (см. рис. 1 и 2) находится как векторная
	V0 12 м/с	сумма составляющих
	V0 12 м/с	V x и V y .
		V x и V y .

	VB , , , n , R -?	V B V x V y
	или

V02Cos 2 Vy2

Составляющую

Vy в точке В

найдём

из

уравнения

(3)

предыдущей

задачи,

подставив

него

время

движения

из

уравнения (8):

VyВ Vo gtB Sin

(Vo sin )2

2gH

Тогда скорость в т. В:

Рис. 2.

			.
VB	VoCos 2 Vo Sin 2 2gH
		Vo2 2gH

Вычисляем

VB 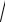122 2 9,81 12 19,5(м/с).

2) Для определения угла , составленного вектором скорости горизонтальной осью X, воспользуемся треугольником скоростей (рис. 2):

Vв с

sin

VyB

Vо Sin 2 2gH

16,5

0,845

;

19,5

V 2

2gH

arcsin 0,845 57 40'

3)Построим в т.B треугольник ускорений. Тангенциальная составляющая

ускорения a направлена вдоль вектора мгновенной скорости V B в данной т. B, т.е. по касательной к траектории.

горизонту

Дано:

, ,V0 .

S, H max .-?

Нормальная составляющая ускорения an направлена перпендикулярно вектору мгновенной скорости VB . Их векторная сумма

a an g

Тогда из рис.2 находим

gSin g

VyB

;

gCos g Vox .

Вычисляем

gSin 9,81. 0,845 8,3 (м/с2),

Cos

9,8

12 0,867

102

5,25 (м/с2).

2 2gH

144 2 9,81 12

19,5

4) Радиус кривизны траектории в точке приземления определяем из уравнения:

an VB 2 , отсюда

R VB 2 19,52 72,5 (м). an 5,25

Ответ: VB 19,5 м/с, 57 40' , a 8,3 м/с2, an 5,25 м/с2, R 72,5 м .

Задача 3.

Камень брошен на склоне горы под углом α к её поверхности (рис.3). Определите дальность полёта камня и его наибольшую высоту подъёма над

склоном, если начальная скорость камня равна β. Сопротивлением воздуха пренебречь.

Си: Решение:

Так же, как и в задаче 1, движение камня, происходящее по параболе, можно

рассматривать как сумму двух независимых прямолинейных движений. В данном случае в качестве составляющих движений удобно брать движения вдоль наклонной плоскости и перпендикулярно к ней. При таком рассмотрении оба составляющих движения прямолинейны и равнопеременны.

Vо, угол наклона горы к

		V0		X
V0 sin		V0
V0 sin			V0 cos
			V0 cos
g sin				S
				S
	g	g cos		Рис. 3.

Поместим начало координат в точке бросания так, чтобы оси OX и OY совпали с указанными направлениями, и найдём составляющие векторов начальной скорости Vо и ускорение свободного падения g по осям. Проекции этих составляющих на оси OX и OY равны соответственно:

ax gSin ; Vox VoCos ;

ay gCos ;Voy Vo Sin .

После этого сложное движение можно рассматривать как два более простых: равнозамедленное движение вдоль наклона горы (поверхности земли) с ускорением gSin и равнопеременное движение, перпендикулярное склону

горы, с ускорением gCos .

Составляем уравнения движения для каждого направления с учётом того, что за время t1 всего движения перемещение камня по нормали к поверхности (по оси OY) оказалось равным 0, а вдоль поверхности (по оси OX) - равным S:

0 V t Sin	gt	2Cos		S V t Cos	gt 2 Sin	.
	1		;		1
	1		;
o 1		2		o 1	2
		2			2

По условию задачи Vo, , нам заданы, поэтому в составленных уравнениях имеются две неизвестные величины S и t1.

Из первого уравнения определяем время полёта камня:

t 2Vо Sin .

1 gCos

Подставляя это выражение во второе уравнени е, находим:

S 2Vо 2 Sin Cos . gCos2

Если подставить сюда значение β=0, что соответствует случаю, когда тело брошено под углом к горизонтальной поверхности, то получим:

S Vо 2 Sin2 . g

Как и следовало ожидать, этот результат совпадает с результатом задачи 1. Самостоятельно предлагается определить максимальную высоту подъёма

камня над поверхностью горы и угол падения.

Задача 4.

Мяч с отвесной скалы высотой 24,5м бросают в горизонтальном направлении с некоторой начальной скоростью. Мяч попадает в цель, лежащую на земле, на расстоянии 30м от основания скалы. С какой начальной скоростью

V0 был брошен мяч и какую конечную скорость VB он приобрёл, попадая в цель?

Дано:		Си:	Решение:
Дано:		Си:	Решение:
S 30 м			Введём координатные оси: по горизонтали OX
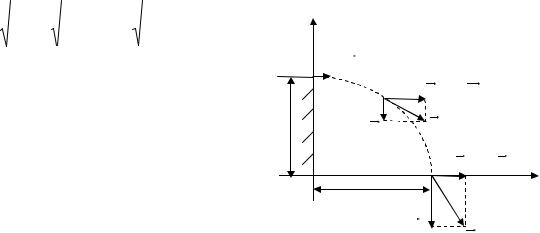
h 24,5	м		и по вертикали OY. Совместим начало координат в т.
h 24,5	м		О (см. рис.4). Рассмотрим движение мяча как сумму
			О (см. рис.4). Рассмотрим движение мяча как сумму
Vo ,VB -?			двух независимых движений: равномерное движение
			по горизонтали (по оси X) и равноускоренное
			по горизонтали (по оси X) и равноускоренное

движение по вертикали (по оси Y). Составим уравнения скорости и перемещения для проекций по каждому направлению.

Так как в горизонтальном направлении мяч летит равномерно, то его скорость и координаты в любой момент времени удовлетворяют уравнениям:

Vx Vox Vo			const ;			(1)
и
X S Vot .						(2)
Для движения мяча по оси Y:
Vy Voy gt ;						(3)
y h V t				gt 2	.	(4)

	oy		2

Т.к. начальная скорость в направлении оси Y Vоy =0 , то уравнения (3) и
(4) преобразуем в уравнения (3 ) и (4 )
Vy gt ,						(3’)
y h	gt 2	.				(4’)

2

Из уравнения (4 ) найдём время полёта t:


t	2h	2 24,5	49	2,24 (c).
	g	9,8	9,8

Зная	время	полёта		мяча,	из	A.	V0
уравнения	(2)	найдём		начальную		A.	V0
уравнения	(2)	найдём		начальную			C	V xc V0
скорость Vо:								V xc V0
скорость Vо:						h	V yc	V c
V S		30				h
			13,3	(м/с).


o	t 2,24					.		.B V xВ V 0 X
	t 2,24
Вычислив VyB из уравнения (3					) и
Вычислив VyB из уравнения (3					) и	O	S
учитывая, что VxB V0 (т.к. движение по							S
учитывая, что VxB V0 (т.к. движение по						Рис. 4		V yВ	V В
						Рис. 4		V yВ

оси X - равномерное) найдём абсолютное значение скорости в т. B:

V		V 2	V 2 yв	13,32 21,92		25,7 (м/с).
	B				658,7
		о

Ответ: Vo = 13,3 м/с, VB = 25,7 м/с.

Задача 5.

Автомобиль движется по закруглению шоссе, имеющему радиус кривизны R 50м. Уравнение движения автомобиля (t) A Bt Ct 2 , где А=10м,

В=10м/с, С 0,5 м/с 2 .

Найти: 1) Скорость автомобиля, его тангенциальное

аτ, нормальное аn и

полное а

ускорение в момент времени

t =5с. 2) Длину пути

и модуль

перемещения

автомобиля

за

интервал время

τ =10с, отсчитанный с

момента начала движения.

Дано:

Си:

Решение:

(t) A Bt Ct 2

1) Зная уравнение движения, найдём

A 10 м

скорость,

взяв

первую

производную

координаты по времени:

В=10м/с

V d B 2Ct.

С 0,5 м/с 2

R 50м

С,

Подставим в это выражение значения В,

t 5 с

произведём

вычисления:

V 10 2 ( 0,5) 5 51(м/с).

10 с

2) Тангенциальное

ускорение

найдём,

V ,an ,a ,a,S, r -?

взяв первую производную скорости по времени:

2C.

Подставив значение C, получим: a 2 ( 0,5) 1(м/с 2 ). 3) Нормальное ускорение определяется по формуле:

an VR2 .

Подставим сюда найденное значение скорости и заданное значение радиуса кривизны траектории и произведём вычисления:

an 52 0,5 (м/с 2 ).

4) Полное ускорение является геометрической

(r)

R r S

О (O)

Рис. 5

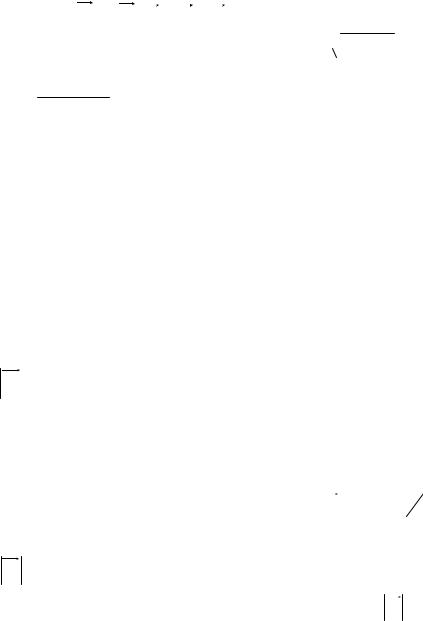
суммой ускорений a и an : a a an .

Абсолютное значение полного ускорения a 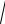a2 an2 . Подставим в это выражение найденные значения a и an :

a12 (0,5)2 1,12 (м/с 2 ).

5)Чтобы определить длину пути S, пройденного автомобилем, заметим, что в случае движения в одном направлении (как это имеет место в условиях

задачи) длина пути S равна изменению криволинейной координаты , т.е.

S 0 , или

S A B C 2 -A=B +C 2 .

Подставим в полученное выражение значения B, C, и произведём вычисления:

S10 10 ( 0,5) 102 50 (м).

6)Модуль перемещения, как это видно из рис.5, равен:

	2R Sin
r	2R Sin	, где
	2
	2

-угол между радиус-векторами, определяющими начальное 0							и конечное
положение автомашины на траектории.
Этот угол (в радианах) находим как отношение длины к пути S							к радиусу
кривизны R траектории, т.е.	S	. Таким образом	r	2R Sin S	2R	.


	R

Подставим сюда значение R, S и произведем вычисления:

r 2 50 Sin0,5 47,9 (м).

Ответ: V=5 м/с, an=-1 м/с2, a =0,5 м/с2,a=1,12 м/с2, S=50 м, r =47,9 м.

III.Вращательное движение

1.Что называется уравнением вращения?

2.Как определяется мгновенная угловая скорость ?

3.Как определить мгновенное угловое ускорение ?

4.Как связаны:

а) угол поворота и длина дуги S, пройденная телом,

б) линейная V и угловая скорости,

в) тангенциальное a и угловое ускорения?

5. Как определяются угловая скорость и угол поворота радиуса (угловой путь) при равнопеременном движении мат ериальной точки по окружности? Записать.

6.Что называется периодом T и частотой вращения n материальной точки по окружности? Как они связаны между соб ой, записать их единицы измерения.

7.Как связаны угловая скорость и период вращения материальной точки T? Записать.

Литература: Т., Гл.1.,§4,C.12, 2000.

Примеры решения задач

Задача 1.

Колесо, вращаясь равнозамедленно, при т орможении уменьшило свою частоту за 1 минуту от 300 до 180 об/мин. Найти угловое ускорение колеса и число оборотов N за это время.

Дано:			Си:
t 1мин		60 с
1 300	об/мин	5	Гц
2 180	об/мин	3	Гц

- ?
N - ?

2 v2 2 v1 t ,

откуда

Решение:

Уравнения, описывающие движение колеса, имеют вид:

0t t 2	,	(1)
2
0 t .		(2)
Приняв во внимание,		что 2 πΝ,

2 , преобразуем уравнение (2):

	2 1 2	,		2 3,14 5 3	0,21	(рад/с 2 ),
	t			60
Учитывая выражение			(1) и (2), находим			число оборотов N вращения

колеса:

2 N 2 1t 2t 2 ,

откуда

N 1t t 2 ; 4

N 5 60 0,21 602 240 об. 4 3,14

Ответ: ε = 0,21 рад/с 2 , N = 240об.

Задача 2.

Тело вращается вокруг неподвижной оси по закону: A Bt Ct 2 , где

А=10рад, В=20рад/с, С=-2

рад/с 2 .

Найти

полное

ускорение

а точки,

находящейся на расстоянии

r 0,1м от оси вращения, для момента времени

t 4 с.

Дано:

Си:

Решение:

A Bt Ct 2

Полное

ускорение

А=10рад

точки,

движущейся по

О. a

кривой

линии,

может

В=20рад/с

быть

найдено,

как

С=-2 рад/с 2

геометрическая

сумма

Рис. 6

r 0,1м

тангенциальной

t 4 с

составляющей ускорения a , направленной по

касательной к траектории, и нормальной

а ?

составляющей ускорения an , направленной к

центру кривизны траектории (рис.6):

a a an

Так как векторы a и

an взаимоперпендикулярны, то модуль ускорения

(1)

Тангенциальная и нормальная составляющие ускорения выражаются формулами:

<<< < Предыдущая 1 23 / 143 4 5 6 7 8 9 10 11 12 13 14 > Следующая >>>