Физика / Физика / Механика. Лекции / Механика. Пособие
.pdf
Примеры решения задач
Задача 1.
Платформа в виде диска радиусом R=1,5 м и массой m1=180 кг вращается по инерции около вертикальной оси с частотой n=10 мин-1. В центре платформы стоит человек массой m2=60 кг. Какую линейную скорость V относительно пола помещения будет иметь человек, если он перейдёт на край платформы?
Дано: |
|
Си: |
|
Решение: |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|||||||
R 1,5 м |
|
|
|
|
|
По закону сохранения момента импульса, |
|||||||||
m 180 кг |
|
|
|
J |
|
J |
|
|
|
|
J |
|
|
, |
(1) |
|
|
|
1 |
2 |
J |
1 |
2 |
|
|||||||
1 |
|
0,17 с-1 |
|
|
|
|
|
|
|
|
|
||||
n 10мин-1 |
|
|
где J1 - момент инерции платформы; J2 – момент |
||||||||||||
m2 60 кг |
|
|
|
инерции человека, стоящего в центре пла тформы; ω |
|||||||||||
|
|
|
|
– |
|
угловая |
скорость |
платформы |
с человеком, |
||||||
V-? |
|
|
|
|
|||||||||||
|
|
|
стоящим в её центре; J1΄ - момент инерции человека, |
||||||||||||
|
|
|
|
||||||||||||
|
|
|
|
||||||||||||
стоящего на краю платформы; ω΄ - угловая скорость платформы с человеком, стоящим на её краю.
Линейная скорость человека, стоящего на краю платформы, связана с
угловой скоростью соотношением |
(2) |
V R . |
|
|
|
Определив ω΄ из уравнения (1) и подставив полученное выражение в формулу
(2) будем иметь:
V |
J1 |
J 2 |
R |
. |
(3) |
||
|
|
J |
|
|
|||
|
|
|
|
|
|||
|
J |
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
Момент инерции платформы рассчитываем как для диска, следовательно,
J1 12 m1R2 .
Момент инерции человека рассчитываем как для материальной точки. Поэтому
J 2 0; J 2 m2 R2 .
Угловая скорость платформы до перехода человека равна :
2 n .
Заменив в формуле (3) величины J1, J2, J2΄ и ω их выражениями, получим:
|
|
|
1 m R2 |
|
|
|
m |
|
||
|
|
|
|
2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|||
V |
|
|
|
|
|
|
2 nR |
|
2 nR . |
|
1 |
2 |
m R2 |
m |
2 |
R2 |
m1 2m2 |
||||
|
|
1 |
|
|
|
|
|
|
||
101
Подставив числовые значения, найдём линейную скорость человека:
V |
|
180 |
|
2 3,14 0,17 1,5 0,942 |
(м/с). |
|
180 2 |
60 |
|||||
|
|
|
|
Ответ: V=0,942 м/с.
Задача 2.
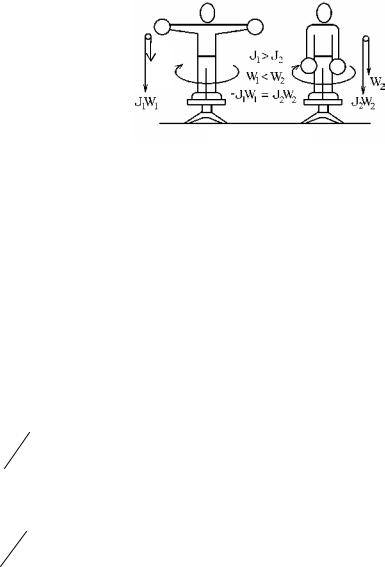
Человек стоит в центре скамьи Жуков ского и вместе с ней вращается по инерции. Частота вращения n1=0,5 с-1. Момент инерции J0 тела человека относительно оси вращения равен 1,6 кг ·м2. В вытянутых в стороны руках человек держит по гире массой m=2 кг каждая. Расстояние между гирями l1=1,6 м. Определить частоту вращения n2 скамьи с человеком, когда он опустит руки и расстояние l2 между гирями станет равным 0,4 м. Моментом инерции скамьи пренебречь.
|
Дано: |
|
|
|
|
Си: |
|
n 0,5с-1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
J0 1,6кг·м2 |
|
|
|
W1 |
|||
m 2 кг |
|
|
|
|
|
|
|
l1 |
1,6 м |
|
|
|
|
|
|
l2 |
0,4 м |
|
|
|
|
|
Рис. 1 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
n2 -? |
|
|
|
|
|
|
|
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Человек, держащий гири (рис.1), составляет вместе со скамьёй замкнутую |
||||||
систему, поэтому момент импульса Jω этой системы должен иметь постоянное |
|||||||
значение. Следовательно, для данного случая: |
|||||||
|
J1 1 |
J 2 2 , |
(1) |
||||
где J1 и ω1 – момент инерции тела человека и угловая скорость скамьи и человека с |
|||||||
вытянутыми руками; |
J2 и ω2 – момент инерции тела человека и угловая скорость |
||||||
скамьи и человека с опущенными руками. |
|||||||
Отсюда |
|
|
|
|
|
|
|
|
|
|
|
J |
1 |
|
|
|
|
|
. |
||||
|
|
2 |
|
|
|
J 2 |
1 |
Выразив в этом уравнении угловые скорости ω1 и ω2 через частоты вращения n1 и n2 2 n и сократив на 2π получим :
n |
|
J |
1 |
|
|
(2) |
|
|
n . |
||||
|
2 |
|
|
J2 |
1 |
|
102
Момент инерции системы, рассматриваемой в данной задаче, равен сумме момента инерции тела человека J0 и момента инерции гирь в руках человека. Так как размер гирь много меньше расстояния их от оси вращения, то момент инерции гирь можно определить по формуле момента инерции материальной точки:
J mr 2 . Следовательно,
J1 J0 2m(l1 2 )2 , J 2 J0 2m(l2 2 )2 ,
где m – масса каждой из гирь; l1 и l2 – первоначальное и конечное расстояние между гирями.
Подставив выражения J1 и J2 в уравнение (2), получим :
|
|
|
J |
|
l |
|
2 |
|
|
|
|
|
|
0 |
2m |
1 |
2 |
|
|
|
|
n |
2 |
|
|
|
|
|
n . |
(3) |
||
|
|
|
|
|
|
|||||
|
|
J0 |
l |
|
|
2 |
1 |
|
||
|
|
|
|
|
|
|
||||
|
|
|
2m |
2 |
2 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
Выполнив по формуле (3) вычисления, найдём :
n2 1,6 2 2 (0,8)2 0,5 1,18 ( с-1). 1,6 2 2 (0,2)2
Ответ: n2=1,18 с-1.
Задача 3.
Маятник в виде однородного шара, жёстко скреплённого с тонким стержнем, длина l которого равна радиусу R шара, может качаться вокруг горизонтальной оси, проходящей через конец стержня (рис.2). В шар нормально к его поверхности ударилась пуля массой m=10 г, летевшая со скоростью V=800 м/с, и застряла в шаре. Масса шара M=10 кг, радиус его R=15см. На какой угол α отклонится маятник в результате удара пули? Массой стержня пренебречь.
Дано: |
Си: |
m 10г |
0,01кг |
V 800м/с |
|
M 10кг |
|
R l 0,15 м |
|
|
|
-? |
|
|
|
сохранения энергии:
Решение:
Как видно из рис. 2, искомый угол α связан с высотой h подъёма центра шара:
Сos 2R h |
. |
(1) |
2R |
|
|
Поскольку в результате удара пули в шар скорости обоих тел станут одинаковыми, этот удар следует считать неупругим. По закону
103
|
2 |
|
|
J |
2 |
Mgh mgh , |
(2), |
где J – момент инерции маятника с застрявшей в нём пулей, h’ – высота подъёма пули.
Строго говоря, не зная, в каком месте шара застряла пуля, мы не можем
вычислить величины J и h’. Однако по условию задачи |
M m , поэтому, |
||||||||||
пренебрегая массой пули по сравнению с массой |
|
|
|
|
|||||||
шара, отбросим величину |
mgh΄ в уравнении |
(2) и |
|
|
|
2R |
|||||
|
|
|
|||||||||
вычислим момент инерции маятника, используя |
l |
|
|
||||||||
|
|
|
|||||||||
теорему Штейнера: |
|
|
|
V |
h |
|
|
|
|||
|
|
|
|
|
|
||||||
|
J 2 |
|
MR2 |
M (2R)2 4,4MR2 . |
(3) |
|
|
|
|||
|
5 |
|
|
|
|
||||||
|
m |
|
M |
||||||||
|
|
|
|
|
|
|
|||||
Теперь определим угловую скорость ω, которую |
|
|
|
Рис.2 |
|||||||
получит |
система |
в |
результате удара |
п ули. |
|
|
|
||||
|
|
|
|
||||||||
Воспользуемся законом сохранения момента импульса. Обозначив через L1 и L2
моменты импульса |
системы соответственно в начале и конце процесса удара, |
можно записать: |
|
L1=L2 . |
(4) |
Величина L1 |
есть момент импульса летящей пули относительно оси |
вращения маятника (сам маятник пока ещё неподвижен). На основании
определения момента импульса J |
mVr |
, имеем |
||||||
L1 mV 2R , |
|
|
|
|
|
(5) |
||
где r 2R . |
|
|
|
|
|
|
|
|
Момент импульса L2 маятника с застрявшей в нём пулей, согласно |
||||||||
определению, равен : |
|
|
|
|
|
|
|
|
L2 J 4,4MR2 . |
|
|
|
|
(6) |
|||
Решая систему (4)-(6) , получаем для угловой скорости : |
||||||||
mV |
2,2MR |
. |
|
|
|
|
(7) |
|
|
|
|
|
|
|
|
|
|
Исключив из системы (1)-(3),(7) неизвестные J, ω , h найдём |
||||||||
Сos 1 m |
2V 2 |
2 |
gR |
|
|
|
|
|
|
|
4,4M |
|
|
|
|
|
|
Подставим численные значения: |
|
|
|
|
||||
Сos 1 0,012 8002 |
4,4 10 |
2 |
10 |
0,15 |
0,9; 26 . |
|||
|
|
|
|
|
||||
Ответ: =26˚ .
104
Задача 4.
С наклонной плоскости скатывается без скольжения однородный диск. Найти ускорение а диска, если угол наклона плоскости к горизонту α=36˚ ; масса диска m=500 г (рис.3).
Дано: Си:
Решение:
При качении без скольжения тело перемеща ется постольку, поскольку оно поворачивается вокруг оси, проходящей через центр масс. Следов ательно,
|
|
|
смещение S центра масс C: |
|||||
|
S r , |
|
|
|
(1) |
|||
где φ – угловое перемещение диска вокруг центра масс. |
||||||||
Дважды дифференцируя это равенство, получим |
|
|||||||
|
Vц.м. r ; |
|
|
|
(2) |
|||
|
aц.м. R , |
|
|
|
(3) |
|||
где ω и ε – угловые скорость |
и ускорение |
вращения тела вокруг оси, |
||||||
проходящей через центр масс C. |
|
|
N |
|||||
Равенства (1),(2),(3) представляют |
||||||||
|
||||||||
собой |
математическую |
запись |
условий |
f тр C . |
||||
качения тела без скольжения (как по |
|
|||||||
наклонной плоскости, так и по любой кривой |
p |
|||||||
поверхности). |
|
|
|
|
|
|
||
|
|
|
|
|
X |
|||
В |
рассматриваемой |
задаче |
на |
диск |
Рис. 3 |
|||
действуют: |
сила |
тяжести |
P , |
сила |
|
|||
нормальной реакции |
N и сила трения |
f тр . Ускорение центра масс a может |
||||||
быть найдено из второго закона Ньютона |
|
|||||||
|
ma P N fтр. . |
|
|
(4) |
||||
Вращение диска вокруг центра масс обуславливается только силой трения, так как моменты силы тяжести и силы нормальной реакции равны нулю. Следовательно, согласно основному закону динамики вращательного движения
J M тр. . |
(5) |
Рассматривая проекции всех сил на ось x (направим ось х вниз параллельно наклонной плоскости), получим на основании уравнения (4) :
ma mgSin fтр. . |
(6) |
Момент силы трения
105
M тр. fтр. r .
Подставляя в уравнение (5) это выражение и равенство (3), получим
J a |
r |
|
fтр. r . |
(7) |
|
|
|
|
При совместном решении уравнений (6) и (7) с учётом, что момент инерции диска
J 12 mr 2 , находим
a mgSin m J |
r |
2 ; |
(8) |
|
|
|
a 23 gSin 23 10 Sin36 3,9 ( м/с2).
Ответ: a=3,9 м/с2.
Задача 5.
Снаклонной плоскости скатываются без скольжения сплошной цилиндр
итележка, поставленная на лёгкие колёса. Массы цилиндра и тележки одинаковы. Какое из тел скатится быстрее и во сколько раз?
|
|
Дано: |
|
|
|
|
|
|
|
Си: |
|
|
|
Решение: |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
m1 m2 m . |
|
|
|
|
|
|
|
|
|
|
|
Движение |
центров |
масс |
обоих |
тел |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
равноускоренное |
без |
начальной |
скорости. |
|||
|
t1 |
? |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Следовательно, для обоих тел можно записать: |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
t2 |
|
|
|
|
|
|
|
|
|
|
|
|
l |
at |
2 |
|
|
|
|
||
или |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
, |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
l |
Vt |
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|||||
2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
где V - скорость тела в конце наклонной плоскости; l – её длина. |
|
|
||||||||||||||||||||
Искомое соотношение времен : |
|
|
|
|
|
|
||||||||||||||||
|
|
|
t1 |
|
V2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
t |
2 |
|
|
V |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Для цилиндра изменения потенциальной EП и кинетической |
EK энергий |
|||||||||||||||||||||
равны: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Eп |
|
mgh , |
|
|
|
|
(1) |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
mV 2 |
2 |
|
|
|
|
|
|
|
|||||
|
|
Eк |
|
|
|
1 |
J |
|
, |
|
|
(2), |
|
|
|
|||||||
2 |
2 |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
106
где h – высота наклонной плоскости; V1 – линейная скорость центра масс для цилиндра; ω – угловая скорость вращения вокруг центра масс в конце наклонной плоскости; J - момент инерции цилиндра.
Известно, что
V1 r,
J mr 2b ,
где коэффициент b для тел разной формы принимает различные значения; для сплошного цилиндра b=1/2.
Определим из этих формул ω и J и подставим в равенство (2), тогда :
Eк |
mV 2 |
1 b . |
(3) |
1 |
|||
|
2 |
|
|
Выражения (1) и (3) подставим в уравнение Eк Eп 0 и окончательно будем иметь выражение для скорости центра масс цил индра:
V |
|
|
2gh |
|
. |
|
|
|
|
|
|
|
|
|
|||
1 |
|
1 b |
|
|
||||
|
|
|
|
|||||
Для тележки изменения потенциальной EП и кинетической |
EK энергий |
|||||||
равны: |
|
|
|
|
|
|
|
|
Eп |
mgh , |
(4) |
|
|||||
Eк |
|
|
|
mV 2 |
|
|
||
|
2 |
. |
(5) |
|
||||
|
|
|||||||
|
|
2 |
|
|
|
|
||
Подставляя выражения (4) и (5) в уравнение
Eк Eп 0 ,
получим, что скорость центра масс тележки
V2 
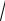2gh . Искомое соотношение времен
t1 |
V2 |
|
|
|
t1 |
|
|
|
|
|
|
, |
|
3 |
|
||||
1 b |
2 |
||||||||
t2 |
t2 |
||||||||
V1 |
|
|
|
|
|
Значит, цилиндр скатывается медленнее, чем тележка.
Ответ: t1 1,2 . t2
Задача 6.
Стержень длиной l 1,5 м и массой М 10 кг может вращаться вокруг неподвижной оси, проходящей через верхний конец стрежня (рис. 4). В середнину стержня ударяет пуля массой m 10г, летящая в горизонтальном
107
направлении со скоростью V0 500 м/с и застревает в стрежне. На какой уголотклонится стержень после удара?
Дано: |
Си: |
|
Решение: |
l 1,5м |
|
|
|
М 10кг |
|
|
Удар пули следует рассматривать как |
|
|
неупругий: после удара и пуля, и соответсвующая |
|
m 0,01кг |
|
|
|
|
|
точка стержня будут двигаться с одинаковыми |
|
V0 500м/с |
|
|
|
|
|
скоростями. |
|
|
|
|
Рассмотрим подробнее явления, происходящие |
-? |
|
|
|
|
|
|
при ударе. Сначала пуля, ударившись о стержень, за |
|
|
ничтожно малый промежуток времени приводит его в движение с угловой скоростью и сообщает ему кинетическую энергию:
T |
J 2 |
, |
(1) |
|
2 |
||||
|
|
|
где J – момент инерции стержня относительно оси вращения.
Затем стержень поворачивается на искомый угол , причем центр масс его поднимается на высоту
h2l (1 Cos ) .
Вотклоненном положении стержень будет обладать потенциальной энергией
П Mg |
l |
(1 Cos ) . |
(2) |
|
|||
2 |
|
|
|
Потенциальная энергия получена за счет кинетической энергии и равна ей по закону сохранения энергии. Приравняв правые част и равенств (1) и (2), получим:
Mg 2l (1 Cos ) J2 2 .
Отсюда:
Cos 1 J 2 . Mgl
Подставим в эту формулу выражение для момента инерции стержня
J |
Ml 2 |
, получим |
|
3 |
|
||
|
|
|
|
Cos 1 l 2 . |
(3) |
||
|
|
3g |
|
108
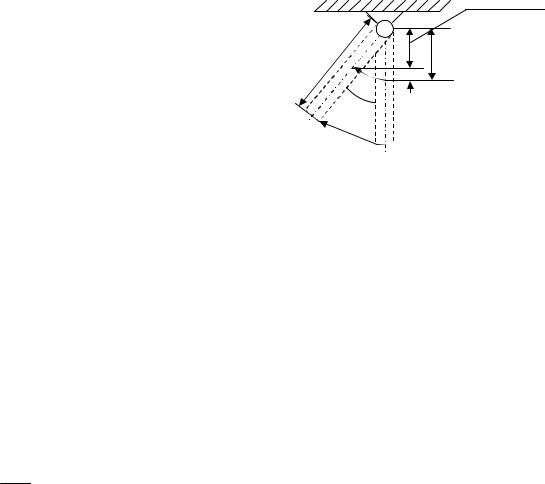
Чтобы из выражения (3) найти необходимо предварительно определить значение . В момент удара на пулю и на стержень действуют силы тяжести, линии действия которых проходят через ось вращения и направлены вертикально вниз. Моменты этих сил относительно оси вращения равны нулю.
Поэтому при ударе пули о стержень будет |
|
|
|
|
|
|
(l / 2)Cos |
|||||
справедлив |
закон |
сохранения момента |
. |
|
|
|
|
|
||||
импульса. |
|
|
|
|
|
|
|
|
l |
|
||
В начальный момент удара угловая |
l .С1 . |
|
|
|
||||||||
|
|
h 2 |
|
|||||||||
скорость |
стержня |
0 0 , |
поэтому |
его |
С |
|
|
|||||
|
|
|||||||||||
момент |
ипульса |
L01 J 0 0. |
Пуля |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
||||||
коснулась стержня и начала углубляться в |
|
|
|
|
|
|
|
|||||
стержень, сообщая ему угловое ускорение и |
Рис. 4 |
|
|
|
|
|
||||||
участвуя во вращении стержня около оси. |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
||||||
Начальный |
момент |
импульса |
пули L02 MV0r , |
где r – |
расстояние точки |
|||||||
попадания от оси вращения. В конечный момент удара стержень имел угловую скорость , а пуля – линейную скорость V , равную линейной скорости точек стрежня, находящихся на расстоянии r от оси вращения. Так как V r , то
конечный момент импульса пули L mVr mr2 . |
||||||||
|
|
|
|
|
|
|
|
2 |
Применив закон сохранения импульса, можем написать: |
||||||||
L |
L |
L L |
2 |
или mV |
r J mr 2 , |
|||
01 |
02 |
|
1 |
0 |
|
|||
откуда |
|
|
|
|
|
|
|
|
|
mV0r |
|
, |
|
|
(4) |
||
J mr 2 |
|
|
|
|||||
где J Ml3 2 момент инерции системы стержень-пуля.
Если учесть,что в (4) mr 2 J |
Ml 2 |
, а также, что |
r |
l |
, то после |
||
3 |
|
||||||
|
|
|
|
2 |
|
||
несложных преобразований получим: |
|
|
|
|
|
||
|
3mV0 |
. |
|
(5) |
|
|
|
|
|
|
|
|
|||
|
2Ml |
|
|
|
|
|
|
Подставив числовые значения величин в (5), н айдем:
3 0,01 500 0,5(c 1 ) . 2 10 1,5
По (3) получим:
109
|
1,5(0,5)2 |
|
|
|
|
|
Cos 1 |
3 9,81 |
0,987, |
9 20 |
. |
||
|
Ответ: =9 20
РЕКОМЕНДУЕМОЕ ЗАДАНИЕ
для в н е а у д и т о р н о г о рассмотрения
1.Кинетическая энергия вала, вращающегося с постоянной скоро стью, соответствующей 5 об/с, равна 60 Дж. Найти момент импульса L этого вала.
Отв. L =3,8 кг·м/с2
2.Платформа в виде диска радиусом R=1 м вращается по инерции с частотой n1=6 мин-1. На краю платформы стоит человек, масса m которого равна 80 кг. С какой частотой n2 , будет вращаться платформа, если человек перейдёт в её центр. Момент инерции J платформы равен 120 кг·м2. Момент инерции человека рассчитывать как для материальной точки.
Отв. 10 мин-1.
3.Человек стоит на скамье Жуковского и ловит рукой мяч мас сой m=0,4 кг, летящий в горизонтальном направлении со скоростью V=20 м/с. Траектория мяча проходит на расстоянии r=0,8 м от вертикальной оси вращения скамьи. С какой угловой скоростью ω начнет вращаться скамья Жуковского с человеком, поймавшим мяч, если су ммарный момент инерции J человека и скамьи равен 6 кг·м2 ?
Отв. 1,02 рад/с.
4.На скамье Жуковского стоит человек и держит в руках стержень длиной l=2,4 м и массой m=8 кг, расположенный вертикально по оси вращения скамьи. Скамья с человеком вращается с част отой n1=1c-1. С какой частотой n2 будет вращаться скамья с человеком, если он повернёт стержень в горизонтальное положение? Суммарный момент инерции J человека и скамьи равен 6 кг·м 2?
Отв. 0,61 c-1.
110