Механика. Пособие

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Ухтинский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

изменилась от значения V0

в первом состоянии до значения V во втором.

Следовательно,

.pdf

Скачиваний:

136

Добавлен:

02.03.2016

Размер:

859.12 Кб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 78 / 148 9 10 11 12 13 14 > Следующая >>>

Fm m a g sin fg cos .

Подставляя значение силы тяги в уравнение (1), найдём:

A m a g sin fg cos S . Подставим числовые значения:

A 3 103 (0,2 10 0,5 0,1 10 0,86) 50 900(кДж). Ответ: A=900 кДж.

2.Мощность

Задача 4.

Самолёт массой т=3т для взлёта должен иметь скорость V=360км/ч и длину разбега S=600м . Какова должна быть минимальная мощность мотора Nmin, необходимая для взлёта самолёта? Силу сопротивления движению считать пропорциональной силе нормального давления, средний коэффициент сопротивления принять равным f 0,2. Движение при разгоне самолёта происходит равноускоренно.

Дано:

Си:

Решение:

360

км/ч

100

м/с

В задаче

требуется

определить

600

мгновенную мощность мотора в

момент

взлёта самолёта. Она и будет

являться той

0,2

минимальной

мощностью,

при

которой

3 т

3 103 кг

самолёт может ещё набрать скорость,

min

необходимую для отрыва от земли:

Nmin FV .

(1)

При разгоне самолёта на его

винт действует со

стороны

отбрасываемого

воздуха сила тяги F , кроме того, к самолёту приложены с ила тяжести

P mg ,

нормальная реакция опоры N и сила сопротивления, равная по условию задачи

f P . Согласно второму закону Ньютона :

F fP ma

или

F fmg ma .

(2)

Поскольку

известны

длина S

разбега самолёта и скорость

при отрыве V,

ускорение a самолёта можно найти из формулы:

a V 2 .	(3)
2S

Исключая из уравнений (1)-(3) неизвестные величины F и а, получим для минимальной мощности:

N		V 2
N	min	m		fg V .
	min		2S
			2S

Подставляя численные значения, получим:

	3	1002
Nmin 3 10			0,2	10	100 3000	(кВт).

		2 600
		2 600

Ответ: Nmin =3000 кВт.

3.Работа в поле силы тяжести

Задача 5.
Камень брошен с высоты h=2м под некоторым углом					к горизонту с
начальной скоростью V0 =6м/с. Найти скорость V камня в момент падения на
землю, если сопротивлением воздуха можно пренебречь.
Дано:		Си:		Решение:
Дано:		Си:		Решение:
h 2 м				Во всё время полёта на камень действует только
V0 =6м/с				сила тяжести mg . Эта сила, как известно, зависит от
				координат камня, поэтому для системы Земля -камень
				применим закон сохранения энергии:

V -?
V -?				Ek Eп 0 ,	(1)

где Ek	и E п
где Ek	и E п		соответственно изменения кинетической и потенциальной
энергий	системы.		Но изменением кинетической энергии		Земли можно

пренебречь; потенциальная энергия системы есть энергия взаимодействия тел, входящих в систему.

Рассмотрим значение каждого слагаемого выражения (1). Скорость камня

где m-масса камня. Потенциальная энергия системы уменьшилась при переходе из первого состояния во второе. Следовательно,

п mgh .

(3)

Подставив выражения (2) и (3) в уравнение (1), получим

V 2 V02 2gh 0.

Откуда

V 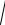V02 2hg 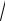62 2 2 10 8,6 (м/с).

Ответ: V=8,6 м/с.

Задача 6.

Ракета установлена на поверхности Земли для запуска в вертикальном направлении. При какой минимальной скорости V1,сообщенной ракете при запуске, она удалится от поверхности на расстояние, равное радиусу Земли (R=6,37 106 м)? Всеми силами, кроме силы гравитационного взаимодействия ракеты и Земли, пренебречь.

			Дано:		Си:	Решение:
			Дано:		Си:	Решение:
R		6	, 37 10	6 м		Минимальную скорость V1 ракеты
g		10	м/с2			можно определить,	зная ее	минимал ьную
						кинетическую энергию Т1. Для определения Т1
V 1	-?					воспользуемся	законом	сохранения
можно записать:						механической энергии. Согласно этому закону
можно записать:
			Т1 П1	Т 2 П2 ,		(1)

где Т1 и П1- кинетическая и потенциальная энергии системы ракета -Земля в начальном состоянии (на поверхности Земли); Т2 и П2- те же величины в конечном состоянии (на расстоянии, равном радиусу Земли).

В рассматриваемом случае центр масс системы ракета -Земля будет практически совпадать с центром Земли, так как масса Земли М много больше массы ракеты. В выбранной системе отсчета кинетическая энергия Земли равна нулю. Поэтому Т1 есть просто начальная кинетическая энергия ракеты:

T1 12 mV 2 .

Потенциальная энергия системы в начальном состоянии

П1 mMR .

По мере удаления ракеты от поверхности Земли ее потенциальна я энергия будет возрастать, а кинетическая - убывать. В конечном состоянии кинетическая энергия Т2 станет равной нулю, а потенциальная энергия П2 достигнет максимального значения

П2 Mm2R .

Подставляя значения Т1, П1, Т2 и П2 в выражение (1), получим:

12 mV12 mMR mM2R , откуда после сокращения на m найдем:

V1 MR .

Заметив, что RM2 g (g-ускорение свободного падения у поверхности

Земли, - постоянная всемирного тяготения), перепишем эту формулу в виде

V1 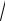gR ,

что совпадает с выражением для первой космической скорости. Подставим числовые значения величин и произведем вычисления:

V	9,8 6,37 10	6	=7,9 103 (м/с).

1

Ответ: V1=7,9 103 м/с.

4.Работа сил упругости

Задача 7.

При выстреле из пружинного пистолета вертикально вверх пуля массой m= 20 г. поднялась на высоту h= 5 м. Определить жесткость k пружины пистолета, если она была сжата на x=10 см. Массой пружины пренебречь.

Дано:	Си:	Решение:
Дано:	Си:	Решение:
m 20 г	0,02 кг	Воспользуемся законом сохранения энергии в
h 5м		механике. Но прежде проследим за энергетическими
h 5м		превращениями, с которыми связан выстрел. При
x 10см	0,1 м	превращениями, с которыми связан выстрел. При
x 10см	0,1 м	зарядке пистолета сжимается пружина и совершается

k -?
k -?		работа А1, в результате чего пружина приобретает
		работа А1, в результате чего пружина приобретает
потенциальную энергию		П1. При выстреле потенциальная энергия пр ужины

переходит в кинетическую энергию Т2 пули, а затем при подъеме ее на высоту h

превращается в потенциальную энергию П2 пули. Если пренебречь потерями
энергии в этой «цепочке»	(A1 П1 Т2 П2 ) энергетических превращений, то
на основе закона сохранения энергии можно записать
А1=П2 .	(1)
Найдем работу А1. Сила F1, сжимающая пружину, является переменной. В
каждый момент она по	направлению противоположна силе упругости F и

численно равна ей. Сила упругости, возникающая в пружине при ее деформации, определяется по закону Гука:

F=k x,

где х- абсолютная деформация пружины. Работу переменной силы вычислим, как сумму элементарных работ. Элементарная работа при сжатии пружины на dx выразится формулой:

dA1=F1dx или dA1=kx dx.

Интегрируя в пределах от 0 до х, получим:

		k x			1 kx2	x	1 kx2 .
A1		k x		xdx	1 kx2	=	1 kx2 .	(2)
			0		2	0	2
			0		2	0	2
Потенциальная энергия пули на высоте h определяется по формуле:
П2=mgh ,							(3)
где g- ускорение свободного падения.
Приравняв (2) и (3) согласно (1), имеем:
kx	2		1
kx			=mgh,
			2
откуда
k=		2mgh .					(4)
			x2

Подставим в формулу (4) значения величин и произведем вычисления:

k= 2 0,02 92,81 5 =196 (H/м).

0,1

Ответ: k=196 Н/м.

5. Закон сохранения механической энергии

Задача 8.

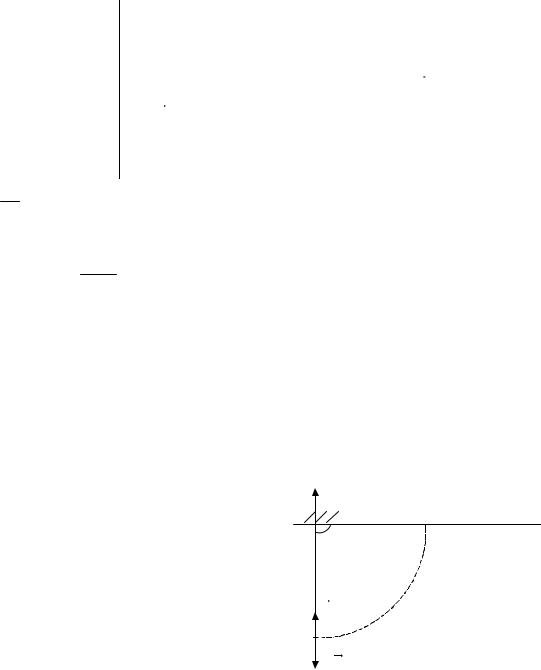
Шар массой m, подвешенный на нерастяжимой нити длиной l отклоняют на угол 900 от вертикали и дают возможность качаться. Определить максимальное натяжение Tmax нити.

Дано:	Си:
m
l
90	1,57рад
Fmp 0

Tmax -?

Решение:

Максимальное натяжение нить испытывает при прохождении шаром точки В (см. рис. 4). В точке В на шар действуют силы: mg - сила тяжести,

T max - сила натяжения.	Запишем для шара
уравнение динамики, относительно оси У.
Тмакс-mg=m y,	(1)

где ay VR2 - нормальное ускорение, R l .

Учитывая это, запишем:

Тмакс-mg= mVl 2 ,

откуда

Тмакс=mg+	mV 2	.	(2)
	l

Скорость шара в точке В определим из закона сохранения энергии для точек А и В:

WA=WB , (3), где

WA=mgl,

mV 2			.
WB=		2	.						Y
Тогда уравнение (3) примет вид:									C .	l	.A
mgl=	mV		2	,
mgl=		2		,
откуда		2
откуда									T max
									T max
V2=2gl.							V2 в		B .
V2=2gl.
Подставив		выражение для							mg		Рис. 4
уравнение (2), получим:									mg		Рис. 4
уравнение (2), получим:
Тмакс=mg+					m2gl	=3mg.		(4)
Тмакс=mg+					l	=3mg.		(4)
					l

Ответ: Тмакс=3mg.

Задача 9.

В покоящийся шар массой М=1 кг, подвешенный на легком несжимаемом стержне, закрепленном в подвесе на шарнире, попадает пуля массой m=0,01 кг.

Угол между направлением полета пули и линией стержня =450. После удара пуля застревает в шаре, и шар вместе с пулей, откачн увшись, поднимается на высоту h=0,2 м относительно первоначального положения. Найти скорость пули V.

Дано:	Си:	Решение:
Дано:	Си:	Решение:
M 1кг		В горизонтальном направлении на пулю и шар
m 0,01кг		внешние	силы не	действуют, поэтому сумма
m 0,01кг		проекций	импульсов	пули и шара на ось ОХ
45		проекций	импульсов	пули и шара на ось ОХ
45		(рис.5,а,б) не меняется:
h 0,2 м		(рис.5,а,б) не меняется:
h 0,2 м

V = ?


		M				h
						h
V
V					u
O .m			O .
O .m		X	O .				X
	а)	Рис. 5		б)
		Рис. 5

M mV·Sin =(M+m)U ,

где U- скорость шара сразу после попадания пули. Отсюда

V	(M m)U .	(1)
	mSin

При максимальном отклонении, согласно закону сохранения энергии, имеем:

(M m)U 2 (M m)gh , 2

откуда:

U 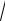2gh .

Подставив это значение в формулу (1), пол учим:

V (M m)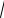2gh , mSin

V (1 0,01)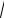2 9,8 0,2 289 (м/с). 0,01 0,71

Ответ: V=289м/с.

6.Упругий удар двух шаров

Задача 11.

На гладкой горизонтальной поверхности на некотором расстоянии от вертикальной стенки находится шар массой М. Второй шар массой m движется от стенки к первому шару. Между шарами происходит центральный упру гий удар. При каком соотношении масс M и m второй шар после удара достигнет стенки и , упруго отразившись от нее, догонит первый шар? Оба шара находятся на одном перпендикуляре к стенке.

Решение:

Пусть V0-скорость второго шара до удара, V1 и V2-скорости первого и второго шаров после удара. При упругом ударе суммарная кинетическая энергия сохраняется:

	mV 2			MV 2		mV 2
	0		=	1	+	2	.	(1)
2				2		2

Пусть		положительное направление						координатной оси сов падает с

направлением вектора V0. Так как вдоль этой оси силы не действуют (трения нет), то суммарная проекция импульсов шаров на эту ось сохраняется:

mV0 MV1 mV2 .

(2)

Систему уравнений (1) и (2) после преобразо ваний запишем в виде: m(V0-V2)(V0+V2)=MV12,

m(V0-V2)=MV1 .

Решив эту систему относительно V1 и V2 получим два ответа:

1) V1=0,			V2=V0 ;
2) V1=	2mV0	,	V2=	m M V0	.
	M m
				M m

Первое решение соответствует ситуации до столкновения шаров. Второе решение дает значения скоростей шаров после удара. Чтобы второй шар после упругого отражения от стенки мог догнать первый шар, необходимо выполнить условия V2>V1,

M m V0	>	2mV0
M m		M m

Отсюда получаем искомое соотношение масс шаров: M>3m.

Ответ: M>3m.

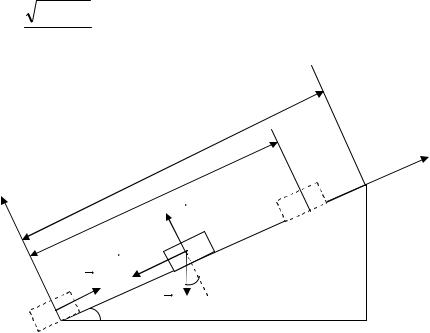
7.Работа силы трения

Задача 12.

Груз начинает скользить с начальной скоростью Vо вверх по наклонной плоскости, имеющей длину l и высоту h. Коэффициент трения равен f. Какой путь S пройдет груз до остановки?

Дано:	Си:	Решение:
		Решение:
			Изменение механической энергии груза равно
V0			Изменение механической энергии груза равно
V0		работе по преодолению силы трения:
l		mV	2	(1)
		mV	-mgh1 =Fтр S,	(1)

h		2
f		где h1-высота, на которой находился груз в момент
		остановки (рис.6)
S - ?		остановки (рис.6)
S - ?			Сила трения

Fтр=fN,

где N-сила реакции плоскости. Из рис.6 сила реакции опоры в проекции на OY:

N=mgСos ,

поэтому

Fтр=f mgСos

Из рис. 6,

l 2 h2

сos = l .

Y		S			A
		N		D
		.		h1	h
					h
	F тр
	V 0
.	V 0
.		P
O			C		B

Рис. 6

Cледовательно,

Fтр= fmg	l 2	h2	.	(2)
Fтр= fmg		l	.	(2)
		l

Из подобия треугольников ОАВ и ОДС следует

	h1	= h	,
	s	= h	,
	s	l
откуда
h1=		hs	.	(3)
		l

Подставим значения (2) и (3) в соотношение (1):

mV 2 =fmg			l 2	h2		S+mg hs
mV 2 =fmg				l		S+mg hs
2				l			l
						V 2l
Отсюда получим S=			2g h f					.
Отсюда получим S=			2g h f				l 2 h2	.
	V 2l
Ответ: S=	2g h f				.
Ответ: S=	2g h f	l 2		h2	.

Задача 13.

Санки съезжают с горы высотой H и углом наклона и движутся дальше по горизонтальному участку. Коэффициент трения на всем пути санок одинаков и равен f. Определить расстояние S, которое пройдут санки по горизонтальному участку до полной остановки.

Дано:	Си:		Решение:
Дано:	Си:		Решение:
H			На основании закона сохранения энергии
f			потенциальная энергия санок расходуется на работу
f			против сил трения на наклонном и горизонтал ьном
			против сил трения на наклонном и горизонтал ьном
			участках (рис. 7):
			участках (рис. 7):
S -?			mgH=Fтр1l+Fтр2S .	(1)
			mgH=Fтр1l+Fтр2S .	(1)
Сила трения на наклонном участке (см. решение предыдущей задачи):
Fтр1= fmgСos ,				(2)
сила трения на горизонтальном участке
Fтр2=fmg.				(3)
Подставляя значения (2) и (3) в равенство (1) и с учетом того, что
l =	H	, получим
l =	Sin	, получим
	Sin

<<< < Предыдущая 1 2 3 4 5 6 78 / 148 9 10 11 12 13 14 > Следующая >>>