
Физика / Физика / Механика. Лекции / Механика. Пособие
.pdf
a |
Fсист |
|
|
mg |
|
, |
|
|
|
|
|
|
|
|
|||
|
mсист |
|
2M m |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
` |
|
|
|
|
|
|
|
|
|
|
|
|
|
P 2M |
|
mg |
|
|
|
2Mmg |
; |
|
|
|
|
||||||
2M m |
2M m |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
||||||||||
T Mg Ma M (g |
|
mg |
) M ( |
2Mg 2mg ) 2Mg |
M m |
; |
|||||||||||
2M m |
2M m |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2M m |
|
|||||
Q 2T 4Mg |
M m |
. |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
2M m |
|
|
|
|
|
|
|
|||||
Задача 4.
Два груза равной массы (m1=m2=1кг), связанные невесомой и нерастяжимой нитью, лежат на идеально гладком столе (рис.9). К первому телу приложена сила F=10 H. Найти силу натяжения нити Т и ускорение а грузов. Нить считать все время натянутой.
Дано: |
|
|
|
Си: |
|
|
|
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
m1 m2 |
1кг, |
|
|
|
|
|
|
На первое тело действуют следующие силы: |
|||||
F 10Н. |
|
|
|
|
|
|
|
m1 g - сила тяжести, N1 - сила реакции стола, |
T1 - |
||||
|
|
|
|
|
|
|
сила натяжения и сила F . Следовательно, |
для |
|||||
|
|
|
|
|
|
|
|
|
|||||
T,a ? |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
первого тела уравнение II закона Ньютона в |
|||||
|
|
|
|
|
|
|
|
|
|||||
векторной форме будет иметь вид: |
|
|
|
|
|||||||||
m g N |
1 |
T F m a |
(1) |
|
l |
|
|||||||
1 |
|
1 |
1 |
1 |
|
Т |
Т |
||||||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
N2 |
|
N 1 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||||
Т 2 |
Т1 |
F |
x |
|
|||
m2 g |
|
m1 g |
Рис. 9. |
|
|
|
На второе тело действуют силы: m2 g - сила тяжести, N2 - сила реакции стола и T2 - сила натяжения второго конца нити. Для второго тела уравнение II закона Ньютона в векторной форме будет иметь вид:
m |
g N |
2 |
T |
m |
a |
2 |
(2) |
2 |
|
2 |
2 |
|
|
41

Выясним соотношение между силами натяжения нити Т1 и Т2. Для этого
рассмотрим |
элемент |
нити |
|
|
1. Так как нить невесома, |
то на элемент 1 |
||||||
действуют только две силы Т и Т , и по II закону Ньютона |
ma = T -T ; если |
|||||||||||
m=0, тогда |
Т =Т . Таким образом, при условии невесомости нити сила |
|||||||||||
натяжения остается постоянной вдоль всей нити, следовательно, |
||||||||||||
Т1 =Т2 =Т . |
|
|
|
|
|
|
|
(3) |
|
|||
Из условия нерастяжимости нити следует, что ускорения обоих тел |
||||||||||||
равны: |
|
|
|
|
|
|
|
|
|
|
|
|
a1 a2 a . |
|
|
|
|
|
|
|
(4) |
|
|||
Выберем направление вправо за положительное, спроецируем силы |
||||||||||||
уравнений (1) и (2) на ось ОХ и, учитывая (3) и (4), получим: |
|
|||||||||||
m1a F T |
|
|
|
|
|
|
|
|
|
|
||
m2a T , откуда |
|
|
|
|
|
|
|
|||||
a |
F |
|
|
, |
T |
|
Fm2 |
. |
|
|||
m m |
|
|
|
|
|
|||||||
|
2 |
|
|
m m |
2 |
|
|
|||||
|
1 |
|
|
|
|
1 |
|
|
|
|||
Подставляя данные условия, получим: |
|
|||||||||||
T |
10 1 |
5(Н); a |
|
|
10 |
|
|
5 (м/с 2 ). |
|
|||
1 1 |
1 1 |
|
||||||||||
|
|
|
|
|
|
|
|
|||||
Ответ: T=5 Н, a=5 м/с2.
Задача 5.
Через блок перекинут шнур, к концам которого подвешены грузы массами m1=1,5кг и m2=3кг. Найти силу давления Fд блока на ось. Массами блока и шнура пренебречь.
Дано: Си: Решение:
m1 1,5кг |
|
|
|
|
|
Сила давления блока (рис. 10) на ось: Fд N , |
|||||
m2 |
3 кг |
|
|
|
где N |
|
- сила реакции оси, действующая на блок и |
||||
|
|
|
|
|
направленная вверх. Кроме |
этой силы |
на |
блок |
|||
Fд |
? |
|
|
|
|||||||
|
|
|
действуют силы натяжения |
нити T1 |
и |
T2 , |
|||||
|
|
|
|
|
|||||||
направленные вниз. Уравнение II закона Ньютона для блока имеет вид: |
|
|
|||||||||
|
m |
бл |
a |
N T T |
m |
бл |
g ,где |
|
|
|
|
|
|
ц |
1 |
2 |
|
|
|
|
|||
aц -ускорение центра масс блока относительн о Земли, mбл -его масса. Если mбл 0 , то независимо от ускорения центра масс
N T1 T2 0 , N=T1+T2.
42
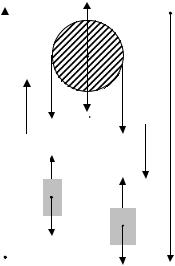
Таким образом, задача сводится к нахождению сил натяжения нити.
Грузы движутся относительно блока под действ ием сил тяжести и натяжения нити. Если нить не растяжима, то ускорения грузов относительно блока одинаковы по модулю, но противоположны по направлен иям. Невесомость нити позволяет считать силу натяж ения вдоль нити постоянной по модулю. Неизменяемость силы натяжения по модулю при переходе через блок может быть доказана при условии, что массой блока можно пренебречь (см. занятие 6, задача 2). Таким образом,
Т1=Т1 =Т2=Т2 .
Выберем для каждого из тел направление движения, проведем оси ОУ, укажем направления ускорения - a (см. рис.10). Запишем уравнения II закона Ньютона для 1 и 2 тела в векторной форме:
m g T |
m a , |
|||
1 |
1 |
1 |
|
|
m |
2 |
g T |
m |
a . |
|
2 |
2 |
|
|
Спроецируем каждое из них на выбранное |
||||
направление ОУ (по направлению движения каждого тела), учитывая, что Т1 =Т2:
m1 g T m1a , |
(1) |
m2 g T m2 a . |
(2) |
Умножая уравнение (1) на m2, а уравнение
(2) на m1, и вычитая из уравнения (1) уравнение (2), получим:
T=(2m1m2g)/(m1+m2).
Искомая сила давления блока на ось:
Fд=N=2T.
Fд (4m1m2 g) /(m1 m2 ) (4 1,5 3 10) / 4,5 40 (Н)
.
Ответ: Fд=40 Н.
y |
N |
О |
|
а Т1 |
|
F д |
|
|
Т2 |
||
|
|
|
|
|
|||
Т1 |
|
|
Т2 |
|
а |
||
|
|
|
|
|
|
||
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m1g |
|
|
|
|
||
|
|
|
m2 g y |
||||
О Рис. 10. |
|
|
|||||
2.Движение в поле тяготения по криволинейной (в простейшем случае - круговой ) траектории
43
При решении задач на динамику движения материаль ной точки по окружности нужно руководствоваться тем же типовым планом решения, что был приведен выше (см. стр.36), но только уравнение II закона Ньютона здесь нужно записывать в форме:
|
|
|
|
V 2 |
|
|
|
2 |
|
|
|
|
|
|
|
||||
|
|
|
|
||||||
|
Fi |
|
m |
|
или |
Fi |
|
m |
R . |
|
|
R |
|||||||
|
|
|
|
|
|
|
|
|
Следует при этом помнить, что вектор суммы всех сил, приложенных к телу, направлен по радиусу к центру окружности. Для нахождения этой суммы (модуля центростремительной силы) необходимо разложить предварительно все силы по линии радиуса и линии, ей перпендикулярной, а зате м найти сумму составляющих по R, которая и будет равна искомой сумме действующих сил.
Задача 6.
Автомобиль с грузом массой 5т проходит по выпуклому мосту со скоростью 21,6км/ч. С какой силой F он давит на середину моста, если радиус кривизны моста 50м?
Дано: |
Си: |
m 5 т |
5 103 кг |
V 21,6 км/ч |
6 м/с |
R 50 м |
|
|
|
F ? |
|
|
|
Решение:
На автомобиль действуют: mg -
сила тяжести, N - сила нормальной реакции моста (рис.11). Направим ось ОУ вертикально по радиусу моста. Запишем для автомобиля уравнение II
закона Ньютона в векторной форме: mg N ma .
Проецируя это равнение на ось ОУ, получим:
mg N may , где ay aц VR2 .
Тогда mg N mV 2 , откуда
R
N mg mV 2 m(g V 2 ). R R
N
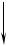 mg
mg
ац
. |
У |
С |
|
|
Рис. 11. |
По третьему закону Ньютона с такой же силой автомобиль будет давить на мост, т.е. F=N или
44
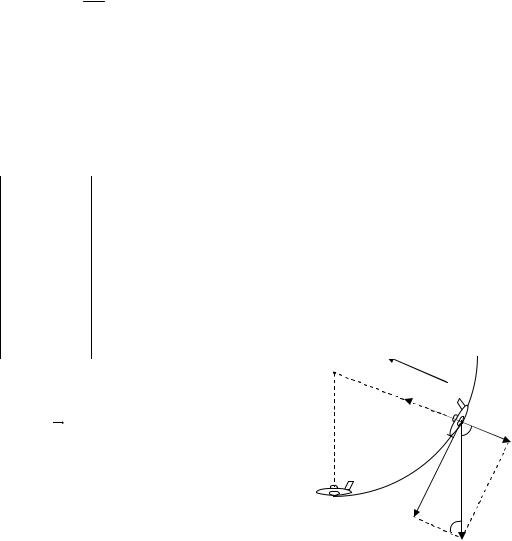
F m(g V 2 ); R
Подставим числовые значения:
F 5 103 (9,8 62 ) 4,5 104 (Н) 50
Ответ: F=4,5 104 Н.
Задача 7.
Определить вес летчика при выходе самолета из пикирования по дуге окружности радиусом 0,5 км, лежащей в вертикальной пло скости, при скорости самолета 600 км/ч. Масса летчика 60 кг.
Дано: Си:
r 0,5 км |
|
500м |
Решение: |
|
|
|
|
|
|
V 600 км/ч |
|
166,7 м/с |
В произвольно взятой точке на летчика |
|
|||||
m 60 кг |
|
|
действуют две силы: mg |
|
- сила тяжести и N - |
|
|||
|
|
сила реакции опоры (кресла) (рис.12). |
|
|
|||||
g 9,8 м/с 2 |
|
|
|
|
|||||
|
|
Разложим силу |
mg на |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
P ? |
|
|
|
|
у |
|
А |
||
|
|
две составляющие: F1 |
|
|
.о |
||||
|
|
|
|
|
О |
||||
и F2 . Центростремительное ускорение обесп ечивают |
|
|
N |
|
|||||
|
|
С |
F1 |
||||||
сила реакции опоры N и составляющая силы тяжести |
|
|
|
|
|||||
F1=mg Cos |
|
|
|
|
|
|
|
|
|
За положительное направление ОУ выберем |
|
В |
|
|
|
||||
направление |
от Земли. Тогда |
уравнение II |
закона |
|
F2 |
|
|
||
Ньютона в векторном виде запишем: |
|
|
|
|
|
||||
|
|
|
|
mg |
|||||
mg N maцс . |
|
|
|
|
Рис. 12. |
||||
|
|
|
|
|
|
||||
Спроецировав силы на ОУ, получим: |
|
|
|
|
|
|
|||
N mgCos maцс . |
|
|
|
|
|
|
|
||
Вес летчика равен силе реакции опоры |
P N (знак минус говорит о |
||||||||
противоположном направлении этих сил), поэтому: P mg(cos V 2 В точке В угол равен нулю , откуда искомый вес :
P mg(1 V 2 / rg).
45
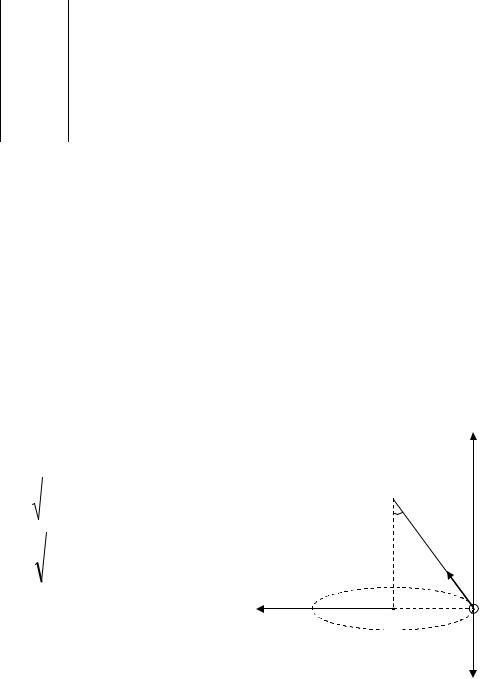
P 60 9,8(1 |
166,7 |
) 3900 (Н) |
|
500 9,8 |
|||
|
|
Ответ: P=3900 H.
Задача 8.
Шарик массой 200 г, привязанный нитью к подвесу, описывает в горизонтальной плоскости окружность, имея постоянную скорость. Определите скорость V шарика и период T его обращения по окружности, если длина нити 1 м, а ее угол с вертикалью составляет 60 .
Дано: Си: Решение:
m 200 г |
|
0,2 кг |
На шарик действуют: mg - сила тяжести, T - |
|
l 1м |
|
|
сила натяжения нити (рис.13). Запишем для шарика |
|
600 . |
|
1,05 рад |
уравнение II закона Ньютона в векторной форме: |
|
|
|
|
mg T ma . |
|
V ,T ? |
|
|
||
|
|
Спроецируем это уравнение на выбранные |
||
|
|
|
||
направления осей ОХ и ОУ: |
|
|||
|
T sin max , |
|
(1) |
|
|
mg T cos may . |
(2) |
||
Учитывая, что ax V 2 / R , |
ay=0 (шарик не движется в вертикальном |
|||
направлении), |
|
|
||
Rl sin ,
иподставляя выражения ах, ау и R в уравнения (1) и (2) , получим:
T sin |
mgV 2 |
|
|
|
; |
|
(3) |
|
|
||||
gl sin |
|
|
|||||||||||
|
|
|
|
|
|
||||||||
T cos mg . |
|
|
|
|
|
(4) |
|
|
|||||
Поделив почленно уравнения |
(3) и (4), |
|
Y |
||||||||||
получим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
V sin |
|
|
|
|
gl |
; |
|
|
|
|
|||
|
|
cos |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V 0,87 |
|
|
|
|
9,8 1 |
|
3,8 |
(м/с) |
|
|
|||
0,5 |
|
|
|
|
Т |
||||||||
|
|
|
|
|
|
|
|
||||||
При равномерном движении шарика |
X |
C . |
|||||||||||
по окружности его период обращения: |
|
|
|||||||||||
46 |
Рис. 13 |
mg |
|
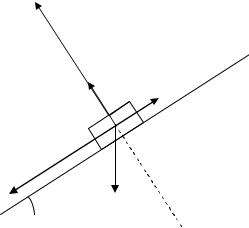
T 2 R V
Поскольку R l sin , то
T |
2 l sin |
; |
T |
2 3,14 1 0,87 |
1,4 (с) |
|
V |
|
|
3,8 |
|
Ответ: V=3,8 м/с, T=1,4 с.
3.Движение в поле тяготения при наличии сил трения
Задача 9.
На наклонную плоскость поместили кубик. Коэффициент трения кубика о плоскость 0,5. Угол наклона плоскости 30 . Найти ускорение a кубика. При каком значении коэффициента трения он останется в покое?
Дано: |
|
Си: |
|
|
|
|
|
|
k 0,5 |
|
|
|
Решение: |
|
|
|
|
300 |
|
|
|
На кубик действуют: |
Y |
|
|
|
|
|
|
|
|
|
|
|
|
g 9,8 м/с 2 |
|
|
|
mg - сила тяжести, Fтр - сила |
|
|
|
|
|
|
|
|
трения и N - сила реакции |
|
|
|
|
a, kmax ? |
|
|
|
|
N |
Fтр |
||
|
|
|
опоры. Изобразим эти силы |
|
||||
|
|
|
|
|
.0 |
|||
на рис.14. Составим уравнение II закона Ньютона в |
|
|
||||||
векторном виде: |
|
|
|
|
|
|||
|
|
|
|
|
|
|||
mg F |
|
N ma |
|
|
|
|||
|
тр |
|
|
|
|
mg |
|
|
Выберем направление оси ОХ вдоль наклонной X |
|
|
||||||
плоскости, а направление ОУ-перпендикулярно к ней. |
|
|
|
|
||||
|
|
|
|
|||||
Найдем проекции сил на выбранные направления осей ОХ и ОУ и запишем скалярные уравнения движения о тносительно этих осей:
mg sin Fтр |
ma , |
(1) |
N mg cos 0 . |
(2) |
|
Из уравнения (2) |
находим, что |
N mg cos . Учитывая, что |
Fтр N mg cos , |
|
|
запишем уравнение (1) |
в виде: |
|
mg sin mg cos ma.
47

Отсюда находим ускорение а: a g sin g cos ;
a 9,8 1/ 2 1/ 2 9,8 
 3 / 2 0,7 ( м/с ) .
3 / 2 0,7 ( м/с ) .
Кубик будет находиться в состоянии покоя на наклонной плоскости, есл и максимальная сила трения покоя больше или равна скатывающей силе (Fтр Fск). Из этого условия найдем коэффициент трения.
max mg cos mg sin , max tg .
0,58.
Примечание: Fск mg sin называют проекцию силы тяжести mg на ось
ОХ.
Ответ: a=0,7м/с2, k 0,58.
Задача 10.
Невесомый блок укреплен на вершине двух наклонных плоскостей,
составляющих |
с горизонтом углы 30 и 45 .Тела массами |
m1=m2=1 кг |
|
соединены нитью. Найти ускорение а, с которым движутся тела, и силу |
|||
натяжения Т нити. Трением пренебречь. Нить нерастяжима. |
|
||
Дано: |
Си: |
Решение: |
|
300 |
|
Свяжем систему координат с каждым из тел: |
|
450 |
|
для первого тела Х1О1У1, для второго тела Х2О2У2 |
|
m1 m2 1кг |
|
(рис.15). Так как по условию задачи массы нити и |
|
|
блока равны нулю, а нить нерастяжима, то |
||
|
|
||
a,T ? |
|
Т1=Т2=Т, а1=а2=а . |
(1) |
|
|
На первое тело действуют силы: m1 g - сила |
|
|
|
||
тяжести, N1 -сила реакции опоры, T1 -сила натяжения нити.
Первое тело движется вниз по наклонной плоскости (если это не так, то ускорение при расчете получится со знаком минус ).
|
|
|
|
х2 |
|
|
у2 |
|
|
|
|
|
|
|
а2 |
у1 |
|
|
|
|
Т 2 |
N2 |
|
N1 |
Т1 |
|
|||||
|
|
|
|||||
|
|
O2 |
|
||||
а1 |
O1 |
|
|
||||
|
|
m2 g |
|||||
|
|
|
|
m1g |
|
|
|
|
|
|
|
|
|
|
|
х1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Рис. 15.
48
Записываем уравнение II закона Ньютона для первого тела в векторной форме:
m |
g N |
1 |
T m a . |
|
|
1 |
|
1 |
1 |
|
|
Спроецировав это уравнение на оси ОХ 1 и ОУ1 , получим |
|||||
m1 g sin T1 m1a , |
(2) |
||||
m1 g cos N1 |
0. |
(3) |
|||
В последнем уравнении справа стоит нуль, так как по напр авлению к оси ОУ1 тело не движется.
Аналогично на второе тело действуют силы: m2 g -тяжести, N2 -реакции
опоры и T2 -натяжения нити.
Записываем уравнение II закона Ньютона для второго тела в вектор ной форме:
m |
g N |
2 |
T m |
a |
|
|
2 |
|
2 |
2 |
|
|
|
Спроецировав это уравнение на оси ОХ 2 и ОУ2, получим: |
||||||
m2 gSin T2 m2a , |
(4) |
|||||
m2 gCos N2 |
0 . |
(5) |
||||
Уравнениями (3) и (5) не пользуются, так как силой трен ия по условию задачи можно пренебречь. Решаем систему уравнений (2) и (4), складывая их почленно
|
m1 gSin T1 m2 gSin T2 |
m1a m2 a , |
|
|
|
|||||||
Откуда с учетом условия (1) получим: |
|
|
|
|
|
|
||||||
a |
m gSin m |
gSin |
|
g(m Sin m |
Sin ) |
|
9,8 (1 sin 45 1 sin 30 |
) |
0,98 |
( м/с ). |
||
1 |
2 |
|
1 |
2 |
|
|
|
|||||
|
m1 m2 |
|
2 |
|
||||||||
|
|
m1 m2 |
|
|
|
|
|
|
|
|||
Из уравнения (2) найдем значение Т:
T=m1gSin -m1a=m1(g Sin -a)=1(9,8 0,7-0,98)=5,9 (H)
Ответ: a=0,98 м/с2; T=5,9 Н.
Задача 11.
Велосипедист движется по горизонтальному пути со скоростью 18 км/ч. Какой минимальный радиус закругления rmin и максимальный наклон max к вертикали может допустить велосипедист, если коэффициент трения скольжения шин 0,3?
49
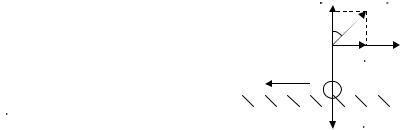
Дано: |
|
Си: |
|
|
Решение: |
|
|
|
|
|
|
|
|
|
|
||||
V 18 км/ч |
|
5 м/с |
|
|
Изобразим систему велосипедист-велосипед |
||||
k 0,3 |
|
|
|
|
схематически |
(рис.16), |
поместив центр |
масс |
|
|
|
|
|
системы в т. |
О, На систему действуют: |
сила |
|||
g 9,8 м/с |
|
|
|
|
|||||
|
|
|
|
тяжести - mg , сила реакции грунта - N , сила трения |
|||||
|
|
|
|
|
|||||
rmin , max ? |
|
|
|
|
- Fтр . |
|
|
|
|
|
|
|
|
|
|
|
N а |
F |
|
За |
положительное |
направление |
ОХ |
||||||
выберем направление по радиусу закругления |
О . |
x |
|||||||
пути велосипедиста. Запишем уравнение II |
F тр |
||||||||
закона Ньютона в векторном виде: |
|
|
|
|
|||||
|
|
|
|
||||||
N Fтр mg maцс . |
|
|
|
mg |
|
||||
Спроецируем силы на ОХ, пол учим: |
|
|
|
||||||
|
|
Рис. 16 |
|
||||||
Fтр=maцс.
При движении велосипедиста именно сила трен ия удерживает велосипед на траектории, не дает ему опрокинуться, т.е. играет роль центростремительной силы. Поэтому
k mg=mV2/rmin .
Отсюда находим значение минимального радиуса закругления (при максимальной силе трения). Максимальный угол наклона αmax будет, если равнодействующая F сил трения и реакции опоры проходит через центр масс системы. Тогда из ONF следует
tg max=Fтр/N . Итак, rmin=V2/ k g,
tg max = k mg/mg= k .
Подставим числовые значения: rmin=25/0,3 9,8 8,3 (м).
max 17 .
Ответ: rmin =8,3 м; max =17 .
РЕКОМЕНДУЕМОЕ ЗАДАНИЕ
для в н е а у д и т о р н о г о рассмотрения
1.В багажнике автомобиля находится груз массой m=42 кг. Автомобиль, едущий со скоростью V0=36 км/ч резко тормозит и останавливается на
50
